Алгоритмы (свойства, реализация алгоритмов)

Алгоритм решения задачи – это система точных и понятных предписаний о содержании и последовательности выполнении конечного числа действий, необходимых для решения любой задачи данного типа.

Алгоритм – это конечный набор правил, последовательное применение, которых к обрабатываемой информации за конечное число шагов позволяет получить результаты обработки (правила выполнения арифметических действий, правила решения определенных видов уравнений и т.д.).

Слово алгоритм появилось в результате искажения (после перевода на европейские языки) имени выдающего математика IX века Аль –Хорезми, которым были описаны правила выполнения основных арифметических действий в десятичной системе счисления. Понятие алгоритма возникло и используется ранее, чем появление ЭВМ.

Основные свойства алгоритма:

1. Дискретность, т.е. пошаговый характер определяемого им процесса. Описываемый процесс должен быть разбит на последовательность отдельных шагов. При каждом шаге работы алгоритма известно, что считать результатом шага.

2. Детерминированность (однозначность или определенность). Процесс применения правил к исходным данным определен вполне однозначно, результат работы алгоритма также будет однозначен. Запись алгоритма должна быть настолько четкой, полной, продуманной в деталях, чтобы у исполнителя не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма.

3. Массовость. Необходимы алгоритмы, обеспечивающие решение широкого класса задач данного типа. Они предполагают возможность использовать различные допустимые значения исходящих данных.

Например: решение уравнения ах2+вх+с=0 в области действительных чисел может быть найдено по формуле:

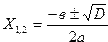, которые применяемы не для одного, а для многих квадратных уравнений с коэффициентами а, в, с, удовлетворяющих условию

D=в2 -4ас 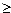0

4. Результативность. При точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.

Под алгоритмизацией понимают процесс разработки алгоритма решения какой-либо задачи.

Формы (способы) записи алгоритмов:

1. Словесный способ алгоритма – содержание последовательных шагов вычислений задается в произвольной форме на естественном языке. Например:

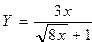
1. Прочитать заданное значение х.

2. Умножить х на 8.

3. Из результата второго действия (шага) извлечь квадратный корень.

4. К результату третьего действия прибавить 1.

5. Умножить х на 3.

6. Результат пятого действия разделить на результат четвертого действия.

7. Записать значение результата у.

Недостатки: низкая наглядность и слабая формализация. Этим способом можно описывать алгоритмы с произвольной степенью детализации.

2. Формульно-словесный способ основывается на задании последовательных шагов алгоритма с помощью математических формул и выражений в сочетании со словесными выражениями. Например:

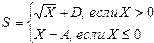
1. Если Х0, то перейти к шагу 2, в противном случае перейти к шагу 3.

2. Положить S= +D. Перейти к шагу 4.

3. Положить S=X-A. Перейти к шагу 4.

4. Принять S за искомый результат и остановиться.

Он более компактен и нагляден, но не является строго формальным.

3. Операторные схемы записи алгоритмов – это аналитическая форма представления алгоритма с помощью операторов, описывающих содержание отдельных участков вычислительного процесса. Участки алгоритма могут разделяться по своему назначению. Одни участки предусматривают вычисления с помощью арифметических операций, другие предназначены для проверки некоторых условий, выполнение которых определяет порядок работы алгоритма. Первые называются арифметическими операторами, вторые – логическими операторами. Имеется также группа специальных операторов управления (ввод-вывод данных, оператор останова и т.д.). Весь процесс решения задач состоит из последовательности выполнения таких операторов. Обозначения операторов.

B- ввод исходных данных

A- арифметический оператор

П — оператор печати (вывода)

Р — логический оператор

Я — оператор останова

Операторы имеют номера-индексы в соответствии с порядком их исследования. Логический оператор записывается как функция, аргументом которой служит проверяемое условие P (i=N) или P(? ?o)и т.д.

Операторы выполняются последовательно, которые могут нарушить логические операторы и безусловные операторы передачи управления. Если окажется, что проверяемое условие истинно, то очередным становится оператор, стоящий справа от логического оператора, в противном случае, когда логическое условие не соблюдается, оператор – приемник указывается стрелкой. Отсутствие передачи управления от оператора слева к соседнему оператору справа обозначается точкой с запятой (;). Алгоритм завершается оператором останова.

Операторная схема алгоритма сопровождается схемой счета.

Например:

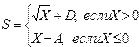
Схема счета представлена в виде таблицы

№	Символ-оператор	Содержание оператора
	В1Р2 А3А4П5Я6	Ввод исходных данныхПроверка выполнения логического условия (X0)Вычисление значения Вычисление значения S= X-AПечать вычисленного значения SОстанов
	Операторная схема выглядит следующим образом	B1 P2 (х0) А3; А4 П5 Я6

Ввел этот метод А.А. Ляпунов в 1954 году. Операторные схемы имеют формальный уровень, близкий к алгоритмическим языкам, и поэтому могут рассматриваться как средство автоматизации программирования.

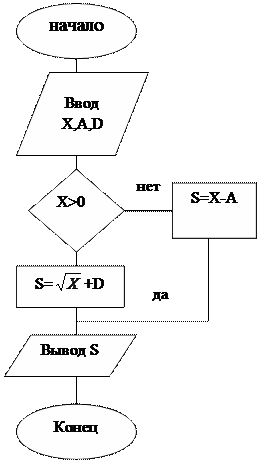
4. Метод блок-схемы – это графическое изображение логической структуры алгоритма. На блок-схеме каждый этап процесса обработки представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера вычисляемых операций. Блоки соединяются стрелками, которые определяют последовательность их выполнения. Этот метод наиболее наглядный и удобный.

Основные виды блоков:

— процесс

— ввод, вывод

— начало, конец (останов)

— магнитный диск

— логические решения

— выходной документ

— магнитная лента

— соединитель

— вывод на экран дисплея

Например:

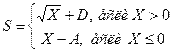
5. Псевдокод или структурно-стилизованный способ записи алгоритма основан на формализованном представлении предписаний. Разновидность: алгоритмический язык в русской нотации. Это например:

алг. запись

арг. истина

если ложь

нач. массив

кон.

Важнейшая особенность – близость к алгоязыкам программирования.

6. Язык программирования используется для записи алгоритмов в виде, непосредственно доступном ЭВМ.

Программа, написанная на языке программирования, представляет собой последовательность операторов, реализующих заданный алгоритм.

Языки программирования высокого уровня: ФОРТРАН, БЕЙСИК, КОБОЛ, АЛГОЛ, ПАСКАЛЬ, СИ, ПЛ/1 и др.

Например:

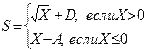
На языке Бейсик это выглядит следующим образом:

10 INPUT «Исх. данные», Х, D, А

20 IF X0 THEN 5 O

30 S=Х- А

40 Goto 6 O

50 S=SQR (X) +D

60 PRINT «Результат=», S

70 END

Структуры данных

При создании нового алгоритма предоставляется так называемый, базовый алгоритм, что является минимально необходимым логическим набором для проведения: элементарных действий с данными. Базовый алгоритм состоит из четырех элементов:

1.начало алгоритма;

2. ввод данных;

3. элемент расчета;

4. конец алгоритма.

При этом, по умолчанию, третий элемент — элемент расчета необходим для того, чтобы явно указать передачу введенных данных в элементе ввода на конечный элемент алгоритма. Тем самым базовый алгоритм позволяет осуществлять передачу данных, получая их из вне, без какой-либо дополнительной математической обработки.

Структуры данных, применяемые в алгоритмах, могут быть чрезвычайно сложными. В результате выбор правильного представления данных часто служит ключом к удачному программированию и может в большей степени сказываться на производительности программы, чем детали используемого алгоритма. Вряд ли когда-нибудь появится общая теория выбора структур данных. Самое лучшее, что можно сделать,- это разобраться во всех вазовых кирпичиках и в собранных из них структурах. Способность приложить эти знания к конструированию больших систем — это прежде всего дело инженерного мастерства и практики.

Начиная изучение структур данных или информационных структур, необходимо ясно установить, что понимается под информацией, как информация передается и как она физически размещается в памяти вычислительной машины.

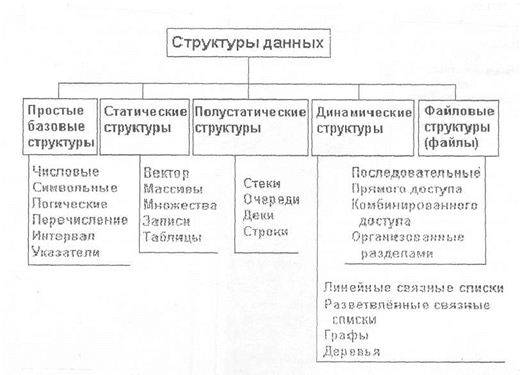
Информация по каждому типу однозначно определяет:

1) структуру хранения данных указанного типа, т ,e. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой;

2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа;

3) множество допустимых операций, которые применимы к объекту описываемого типа.

В вычислительной технике структура данных — это программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих интерфейс структуры данных. Структуры данных формируются с помощью типов данных, ссылок и операций над ними в выбранном языке программирования.

Массив — упорядоченный набор данных, для хранения данных одного типа, идентифицируемых с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа. Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике., двумерный — матрице. Чаще всего применяются массивы с одним или двумя индексами, реже — с тремя, ещё большее количество индексов встречается крайне редко.

Тип (сорт) — относительно устойчивая, независимая совокупность элементов, которую можно выделить во всем рассматриваемом множестве (предметной области} Типы данных бывзют следующие:

Простые.

Перечислимый тип может хранить только те значения, которые прямо указаны в его описании:

-Числовые. Хранятся числа. Могут применяться обычные арифметические операции.

-Целочисленные: со знаком, то есть могут принимать как положительные, так и отрицательные значения; и без знака, то есть могут принимать только неотрицательные значения.

-Вещественные: с запятой (то есть хранятся знак и цифры целой и дробной частей) и с плавающей запятой (то есть число приводится к виду m*2е, где m — мантисса, е — экспонента, причем 1/2

— Числа произвольной точности, обращение с которыми происходит посредством длинной арифметики.

-Символьный тип. Хранит один символ. Могут использоваться различные кодировки.

-Логический тип. Имеет два значения: истина и ложь. Могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипом числового типа, при этом ложь=0, истина=1.

-Множество. В основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип.

Составные (сложные).

-Массив. Является индексированным набором элементов одного типа. Одномерный массив — вектор, двумерный массив — матрица.

-Строковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенация (прибавление одной строки в конец другой строки). В языках, близких к бинарному представлению данных, чаще рассматривается как массив символов, в языках более высокой абстракции зачастую выделяется в качестве простого.

-Запись (структура). Набор различных элементов (полей записи), хранимый как единое целое. Возможен доступ к отдельным полям записи. Например, struct в С или record в Pascal.

-Файловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включённый в некоторые системы программирования, фактически является неявным массивом).

Алгоритмические структуры

Теория алгоритмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.

Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). была предложена Аланом Тьюрингом в 1936_ходу для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

Устройство машины Тьюринга

В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара (ленточный символ — состояние), для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.

Описание машины Тьюринга

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита А, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj®qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква аj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурацииимеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

Варианты машины Тьюринга

Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.

Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:

— линейные

— ветвящиеся

— циклические

Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.

Каждая операция является самостоятельной, независимой от каких-либо условий.

Линейные вычислительные процессы имеют место при вычислении арифметических выражений.

Пример 1:

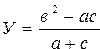
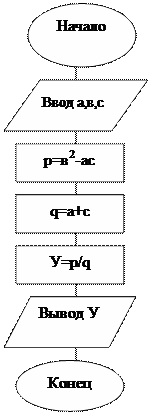
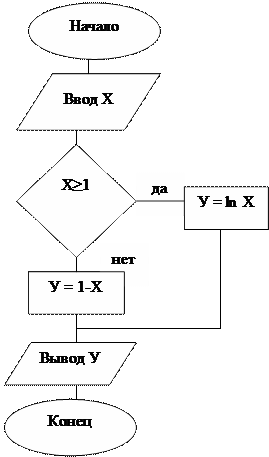
Ветвящимся называется такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.

В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.

Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.

Направления ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено, «нет» -условие не выполнено.

Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.

Пример 2:

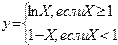
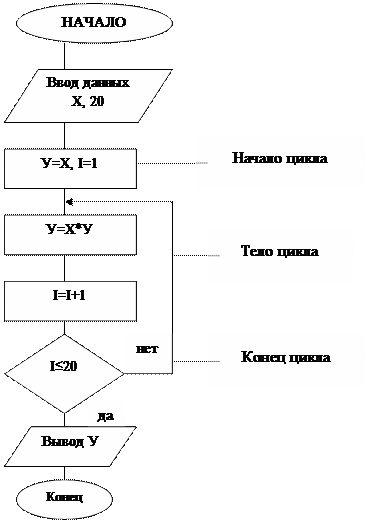
При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.

Пример 3:

У=X20

Анализ алгоритмов

Целью анализа трудоемкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.

Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.

Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. Используемая в асимптотическом анализе оценка функции трудоёмкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоёмкость алгоритма с увеличением объема данных. В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе.

[kgl]

[gl] Тема 6. Знакомство с языками программирования. [:]

Статьи к прочтению:

Алгоритмы. Виды и свойства алгоритмов

Похожие статьи: