Длинная арифметика с.м. окулов
Известно, что арифметические действия, выполняемые компьютером в ограниченном числе разрядов, не всегда позволяют получить точный результат. Более того, мы ограничены размером (величиной) чисел, с которыми можем работать. А если нам необходимо выполнить арифметические действия над очень большими числами, например,
30! = 265252859812191058636308480000000?
В таких случаях мы сами должны позаботиться о представлении чисел в машине и о точном выполнении арифметических операций над ними.
Числа, для представления которых в стандартных компьютерных типах данных не хватает количества двоичных разрядов, называются длинными. Реализация арифметических операций над такими длинными числами получила название длинной арифметики.
Организация работы с длинными числами во многом зависит от того, как мы представим в компьютере эти числа. Длинное число можно записать, например, с помощью массива десятичных цифр, количество элементов в таком массиве равно количеству значащих цифр в длинном числе. Но если мы будем реализовывать арифметические операции над этим числом, то размер массива должен быть достаточным, чтобы разместить в нем и результат, например, умножения.
Существуют и другие представления длинных чисел. Рассмотрим одно из них. Представим наше число
30! = 265252859812191058636308480000000
в виде:
30! = 2 * (104)8 + 6525 * (104)7 + 2859 * (104) + 8121 * (104)5 + 9105 * (104)4 + 8636 * (104)3 + 3084 * (104)2 + 8000 * (104)1 + 0000 * (104)0.
Это представление наталкивает на мысль о массиве, представленном в табл. 1.
Таблица 1
| Номер элемента в массиве А | ||||||||||
| Значение |
Мы можем считать, что наше длинное число представлено в 10000-10 системе счисления (десятитысячно-десятичная система счисления, приведите аналогию с восьмерично-десятичной системой счисления), а цифрами числа являются четырехзначные числа.
Возникают вопросы. Что за 9 в А [0], почему число хранится задом наперед? Ответы очевидны, но подождем с преждевременными объяснениями. Ответы на вопросы будут ясны из текста.
Примечание. Мы работаем с положительными числами!
Первая задача. Ввести длинное число из файла. Решение задачи начнем с описания данных.
Const MaxDig = 1000; {Максимальное количество цифр — четырехзначных!} Osn = 10000; {Основание нашей системы счисления, в элементах массива храним четырехзначные числа} Type Tlong = Array[0..MaxDig] Of Integer; {Максимальное количество десятичных цифр в нашем числе}
Алгоритм ввода длинного числа из файла рассмотрим на конкретном примере.
Пусть в файле записано число 23851674 и основанием (Osn) является 1000 (храним по три цифры в элементе массива А). Изменение значений элементов массива А в процессе ввода (посимвольного в переменную Ch) отражено в табл. 2.
Таблица 2
| А[0] | А[1] | А[2] | А[3] | Ch | Примечание |
| — | Конечное состояние | ||||
| Начальное состояние | |||||
| 1-й шаг | |||||
| 2-й шаг | |||||
| 3-й шаг | |||||
| 4-й шаг: старшая цифра элемента А [1] перешла в пока пустой элемент А[2] | |||||
| 5-й шаг | |||||
| 6-й шаг | |||||
| 7-й шаг | |||||
Проанализируем таблицу (и получим ответы на поставленные выше вопросы).
1. В А[0] храним количество задействованных (ненулевых) элементов массива А — это уже очевидно.
2. При обработке каждой очередной цифры входного числа старшая цифра элемента массива с номером i становится младшей цифрой числа в элементе i + 1, а вводимая цифра будет младшей цифрой числа из А[1]. В результате работы нашего алгоритма мы получили число, записанное задом наперед.
Примечание (методическое): Можно ограничиться этим объяснением и разработку процедуры вынести на самостоятельное задание. Можно продолжить объяснение. Например, выписать фрагмент текста процедуры перенос старшей цифры из A[i] в младшую цифру А[i+1], т.е. сдвиг уже введенной части числа на одну позицию вправо:
For i := A[0] DownTo 1 Do Begin A[i+l] := A[i+l] + (Longint(A[i]) * 10) Div Osn; A[i] := (LongInt(A[i]) * 10) Mod Osn; End;
Пусть мы вводим число 23851674 и первые 6 цифр уже разместили задом наперед в массиве А. В символьную переменную считали очередную цифру длинного числа — это 7. По нашему алгоритму эта цифра 7 должна быть размещена младшей цифрой в А[1]. Выписанный фрагмент программы освобождает место для этой цифры. В таблице отражены результаты работы этого фрагмента.
| i | А[1] | А[2] | А[3] | ch |
После этого остается только добавить текущую (считанную в ch) цифру длинного числа к А[1] и изменить значение А[0].
В конечном итоге процедура должна иметь следующий вид:
Procedure ReadLong(Var A : Tlong); Var ch : char; i : Integer; Begin FillChar(A, SizeOf(A), 0) ; Read(ch); While Not(ch In [‘0’..’9′]) Do Read(ch); {пропуск не цифр во входном файле} While ch In [‘0’..’9′] Do Begin For i := A[0] DownTo 1 Do Begin {протаскивание старшей цифры в числе из A[i] в младшую цифру числа из A[i+l]} A[i+l] := A[i+l] + (LongInt(A[i]) * 10) Div Osn; A[i] := (LongInt(A[i]) * 10) Mod Osn End; A[1] := A[l] + Ord(ch) — Ord(‘0’); {добавляем младшую цифру к числу из А[1]} If A[A[0]+1]0 Then Inc(A[0]); {изменяем длину, число задействованных элементов массива А} Read(ch) End End;
Вторая задача. Вывод длинного числа в файл или на экран.
Казалось бы, нет проблем — выводи число за числом. Однако в силу выбранного нами представления длинного числа мы должны всегда помнить, что в каждом элементе массива хранится не последовательность цифр длинного числа, а значение числа, записанного этими цифрами. Пусть в элементах массива хранятся четырехзначные числа. Тогда длинное число 128400583274 будет в массиве А представлено следующим образом:
| A[0] | A[1] | A[2] | A[3] |
При выводе длинного числа из массива нам необходимо вывести 0058, иначе будет потеря цифр. Итак, незначащие нули также необходимо выводить. Процедура вывода имеет вид:
Procedure WriteLong(Const A : Tlong); Var ls, s : String; i : Integer; Begin Str(Osn Div 10, Is); Write(A[A[0]]; {выводим старшие цифры числа} For i := A[0] — l DownTo 1 Do Begin Str(A[i], s); While Length(s)Length(Is) Do s := ‘0’ + s; {дополняем незначащими нулями} Write(s) End; WriteLn End;
Третья задача. Предварительная работа по описанию способа хранения, вводу и выводу длинных чисел выполнена.
У нас есть все необходимые кирпичики, например, для написания программы сложения двух длинных положительных чисел. Исходные числа и результат храним в файлах. Назовем процедуру сложения SumLongTwo.
Тогда программа ввода двух длинных чисел и вывода результата их сложения будет иметь следующий вид:
Var A, B, C : Tlong; Begin Assign(Input, ‘Input.txt’); Reset(Input); ReadLong(A); ReadLong(B) ; Close(Input); SumLongTwo(A, B, C); Assign(Output, ‘Output.txt’); Rewrite(Output); WriteLong(C); Close(Output) End.
Алгоритм процедуры сложения можно объяснить на простом примере. Пусть А = 870613029451, В = 3475912100517461.
| i | A[i] | B[i] | C[1] | C[2] | C[3] | C[4] |
Алгоритм имитирует привычное сложение столбиком, начиная с младших разрядов. И именно для простоты реализации арифметических операций над длинными числами используется машинное представление задом наперед.
Результат: С = 3476782713546912.
Ниже приведен текст процедуры сложения двух длинных чисел.
Procedure SumLongTwo(A, B : Nlong; Var C : Tlong); Var i, k : Integer; Begin FillChar(C, SizeOf (C), 0) ; If A[0]B[0] Then k := A[0] Else k : =B[0]; For i := l To k Do Begin С [i+1] := (C[i] + A[i] + B[i]) Div Osn; C[i] := (C[i] + A[i] + B[i]) Mod Osn {Есть ли в этих операторах ошибка?} End; If C[k+l] = 0 Then C[0] := k Else C[0] := k + l End;
Четвертая задача. Реализация операций сравнения для длинных чисел (А = В, АВ, А = В).
Function Eq(A, B : TLong) : Boolean; Var i : Integer; Begin Eq := False; If A[0]B[0] Then Exit Else Begin i := l; While (i Реализация функции АВ также прозрачна.Function More(A, B : Tlong) : Boolean; Var i : Integer; Begin If A[0]B[0] Then More := True Else Begin i := A[0]; While (i0) And (A[i] = B[i]) Do Dec(i); If i = 0 Then More := False Else If A[i]B[i] Then More := True Else More:=False End End;
Остальные функции реализуются через функции Eq и More.
Function Less(A, B : Tlong) : Boolean; {A = B} Begin More_Eq := More(A, B) Or Eq(A, B) End; Function Less_Eq(A, B : Tlong) : Boolean; {A Для самостоятельного решения может быть предложена следующая, более сложная, задача. Требуется разработать функцию, которая выдает 0, если А больше В, 1, если А меньше В, и 2 при равенстве чисел. Но сравнение должно быть выполнено с учетом сдвига. О чем идет речь? Поясним на примере. Пусть А равно 56784, а В — 634. При сдвиге числа В на 2 позиции влево функция должна сказать, что В больше А, без сдвига, что А больше В. Другой пример. При А равном 56700, а В — 567 и сдвиге 2 функция должна сказать, что числа равны. Решение может иметь следующий вид:Function More(Const А, В : Tlong; Const sdvig : Integer) : Byte;Var i : Integer;Begin If A[0]B[0] + sdvig Then More := 0 Else If A[0]sdvig) And (A[i] = B[i-sdvig]) Do Dec(i); If i = sdvig Then Begin More:=0; {совпадение чисел с учетом сдвига} For i := 1 To sdvig Do If A[i]0 Then Exit; More := 2; {числа равны, хвост числа А равен нулю} End Else More := Byte(A[i]B[i-sdvig]) EndEnd;
Пятая задача. Умножение длинного числа на короткое. Под коротким понимается целое число типа LongInt.
Процедура очень походит на процедуру сложения двух длинных чисел.
Procedure Mul(Const A : TLong; Const К : Longlnt; Var С : TLong); Var i : Integer; {результат — значение переменной С} Begin FillChar (С, SizeOf(С), 0); If K = 0 Then Inc(С[0]){умножение на ноль} Else Begin For i:= l To A[0] Do Begin C[i+l] := (LongInt(A[i]) * K + C[i]) Div Osn; C[i] := (LongInt(A[i])* K + C[i]) Mod Osn End; If C[A[0]+1]0 Then C[0]:= A[0] + 1 Else C[0]:= A[0] {определяем длину результата} End End;
Шестая задача. Вычитание двух длинных чисел с учетом сдвига
Если понятие сдвига пока не понятно, то оставьте его в покое, на самом деле вычитание с учетом сдвига потребуется при реализации операции деления. В начале выясните логику работы процедуры при нулевом сдвиге.
Введем ограничение: число, из которого вычитают, больше числа, которое вычитается. Работать с длинными отрицательными числами мы не умеем.
Процедура была бы похожа на процедуры сложения и умножения, если бы не одно но — заимствование единицы из старшего разряда вместо переноса единицы в старший разряд. Например, в обычной системе счисления мы вычитаем 9 из 11 — идет заимствование 1 из разряда десятков, а если из 10000 вычитаем 9 — процесс заимствования несколько сложнее.
Procedure Sub (Var A : TLong; Const B : TLong; Const sp : Integer); Var i, j : Integer; {из А вычитаем В с учетом сдвига sp, результат вычитания в А} Begin For i := l To B[0] Do Begin Dec(A[i+sp], B[i]); j: = i;{*} {реализация сложного заимствования} while (A[j+sp]0) and (j Рекомендуется выполнить трассировку работы данной процедуры, например, для следующих исходных данных. Число А равно 100000001000000000000, число В — 2000073859998.
Седьмая задача. Деление двух длинных чисел, т.е. нахождение целой части частного и остатка.
Написать исходную (без уточнений) часть логики не составляет труда. Это:
Procedure Long_Div_Long(Const А, В : TLong; Var Res, Ost : TLong); Begin FillChar(Res, SizeOf(Res), 0); Res[0] := 1; FillChar(Ost, SizeOf(Ost), 0); 0st[0] := 1; Case More(A, B, 0) Of 0: MakeDel(A, B, Res, Ost); {А больше В, пока не знаем, как выполнять операцию — выносим в процедуру} 1: Ost:=A; {А меньше В} 2: Res[l] := l; {А равно В} End; End;
А дальше? Дальше начинаются проблемы. Делить столбиком нас научили в школе. Например,
1000143123567 |73859998 — 73859998 |———- ——— |13541 (Целая часть частного) 261543143 — 221579994 ———- 399631495 — 369299990 ——— 303315056 — 295439992 ———- 78750647 — 73859998 ——— 4890649 (Остаток)
Что мы делали? На каждом этапе в уме подбирали цифру (1, 3, 5 и т.д.), такую, что произведение этой цифры на делитель дает число меньшее, но наиболее близкое к числу… Какому? Это трудно сказать словами, но из примера ясно. Зачем нам это делать в уме, пусть делает компьютер. Однако упростим пример, оставим его для тестирования окончательной логики процедуры, тем более что и числа длинные. Пусть число А будет меньше В * 10, тогда в результате (целой части деления) будет одна цифра. Например, А равно 564, а В — 63 и простая десятичная система счисления. Попробуем подобрать цифру результата, но не методом прямого перебора, а методом деления отрезка пополам. Пусть Down — верхняя граница интервала изменения подбираемой цифры, Up — нижняя граница интервала, Ost равен делимому.
| Down | Up | С = В * ( (Down + Up) Div 2) | Ost = 564 |
| 315 = 63 * ( (0 + 10) Div 2) | COst | ||
| 441 = 63 * ( (5 + 10) Div 2) | COst | ||
| 504 = 63 * ( (7 + 10) Div 2) | COst | ||
| 567 = 63 * ( (8 + 10) Div 2) | COst | ||
| 504 = 63 * ( (8 + 9) Div 2) | COst |
Итак, результат — целая часть частного — равен (Up + Down) Div 2, остаток от деления — разность между значениями Ost и С. Нижнюю границу (Down) изменяем, если результат (С) меньше остатка, верхнюю (Up), — если больше.
Усложним пример. Пусть А равно 27856, а В — 354. Основанием системы счисления является не 10, а 10000.
| Down | Up | С | Ost = 27856 |
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst | |||
| COst |
Целая часть частного равна 78, остаток от деления — 27856 минус 27612, т.е. 244.
Пора приводить процедуру. Используемые кирпичики: функция сравнения чисел (More) с учетом сдвига и функция умножения длинного числа на короткое (Mul) описаны выше.
Function FindBin(Var Ost : Tlong; Const В : TLong; Const sp : Integer) : Longint;Var Down, Up : Word; C : TLong;Begin Down := 0;Up := 0sn; {основание системы счисления} While Up — lDown Do Begin {Есть возможность преподавателю сделать сознательную ошибку. Изменить условие цикла на UpDown. Результат — зацикливание программы.} Mul(В, (Up + Down) Div 2, С); Case More(Ost, C, sp) Of 0: Down := (Down + Up) Div 2; 1: Up := (Up + Down) Div 2; 2: Begin Up := (Up + Down) Div 2; Down := Up End; End; End; Mul(B, (Up + Down) Div 2, C); If More (Ost, C, 0) = 0 Then Sub(Ost, C, sp) {находим остаток от деления} Else begin Sub (C, Ost, sp); Ost := C end; FindBin := (Up + Down) Div 2; {целая часть частного}End;
Осталось разобраться со сдвигом, значением переменной sp в нашем изложении. Опять вернемся к обычной системе счисления и попытаемся разделить, например, 635 на 15. Что мы делаем? Вначале делим 63 на 15 и формируем, подбираем в уме первую цифру результата. Подбирать с помощью компьютера мы научились. Подобрали — это цифра 4, и это старшая цифра результата. Изменим остаток. Если вначале он был 635, то сейчас стал 35. Вычитать с учетом сдвига мы умеем. Опять подбираем цифру. Вторую цифру результата. Это цифра 2 и остаток 5. Итак, результат (целая часть) 42, остаток от деления 5. А что изменится, если основанием будет не 10, а 10000? Логика совпадает, только в уме считать несколько труднее, но ведь у нас же есть молоток под названием компьютер — пусть он вбивает гвозди.
Procedure MakeDel(Const А, В : TLong; Var Res, Ost : TLong);Var sp : Integer;Begin Ost := A; {первоначальное значение остатка} sp := А[0] — В[0]; If More(А, В, sp) = l Then Dec(sp); {B * OsnA, в результате одна цифра} Res[0] := sp + l; While sp = 0 Do Begin {находим очередную цифру результата} Res[sp + 1] := FindBin(Ost, B, sp); Dec(sp) EndEnd;
Методические рекомендации. Представленный материал излагается на четырех занятиях по известной схеме: 10-15-минутное изложение идей, а затем работа учащихся под руководством преподавателя.
1-е занятие. Ввод, вывод и сложение длинных чисел (задачи 1, 2, 3).
2-е занятие. Функции сравнения (задача 4).
3-е занятие. Умножение и вычитание длинных чисел (задачи 5, 6).
4-е занятие. Деление длинных чисел (задача 7). Безусловно, эта схема не догма. В зависимости от уровня подготовки учащихся на самостоятельное выполнение может быть вынесена значительная часть материала. Замечу только, что в силу сложившейся традиции в ряде случаев допускаются при изложении сознательные ошибки. В результате работы каждый учащийся должен иметь собственный модуль для работы с длинными числами.
Темы для исследований
1. Решение задач: поиск наибольшего общего делителя двух длинных чисел; поиск наименьшего общего кратного двух длинных чисел; извлечение квадратного корня из длинного числа и т.д.
2. Длинные числа могут быть отрицательными. Как изменятся описанные выше операции для этого случая?
3. Для хранения длинных чисел используется не массив, а стек, реализованный с помощью списка. Модифицировать модуль работы с длинными числами.
Вычисление степени
При возведении целого числа в неотрицательную степень обычно используют определение степени, т.е. в цикле многократно умножают число на себя. Однако для длинных чисел этот алгоритм не является эффективным. Поэтому целесообразно использовать алгоритмы меньшей сложности, например, описаный ниже.
(Из книги А. Шеня Программирование: теоремы и задачи.) Дано целое число а и целое неотрицательное число n. Вычислить а в степени n. Другими словами, необходимо составить программу, при исполнении которой значения переменных а и n не меняются, а значение некоторой другой переменной (например, b) становится равным а в степени n. (При этом разрешается использовать и другие переменные.) Требуется, чтобы число действий (выполняемых операторов присваивания) было порядка log2 n (то есть не превосходило бы C * log2 n для некоторой константы C; log2 n — это степень, в которую нужно возвести 2, чтобы получить n).
Решение.
k := n; b := 1; c := a; {a в степени n = b * (c в степени k)} while k0 do begin if k mod 2 = 0 then begin k := k div 2; c := c * c end else begin k := k — 1; b := b * c end end;
Каждый второй раз (не реже) будет выполняться первый вариант оператора выбора (если k нечетно, то после вычитания единицы становится четным), так что за два цикла величина k уменьшается по крайней мере вдвое.
Правило извлечения квадратного корня из натурального числа
(Из книги Гусева В.А., Мордковича А.Г. Математика: Справ. материалы: Кн. для учащихся. — 2-е изд. — М.: Просвещение, 1990. — 416 с.)
Пусть нужно извлечь квадратный корень из натурального числа m, причем известно, что корень извлекается. Чтобы найти результат, иногда удобно воспользоваться следующим правилом.
1. Разобьем число m на грани (справа налево, начиная с последней цифры), включив в каждую грань по две рядом стоящие цифры. При этом следует учесть, что если m состоит из четного числа цифр, то в первой (слева) грани будет две цифры; если же число m состоит из нечетного числа цифр, то первая грань состоит из одной цифры. Количество граней показывает количество цифр результата.
2. Подбираем наибольшую цифру, такую, что ее квадрат не превосходит числа, находящегося в первой грани; эта цифра — первая цифра результата.
3. Возведем первую цифру результата в квадрат, вычтем полученное число из первой грани, припишем к найденной разности справа вторую грань. Получится некоторое число A. Удвоив имеющуюся часть результата, получим число а. Теперь подберем такую наибольшую цифру x, чтобы произведение числа 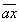 (запись
(запись 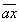 означает 10 * a + x) на x не превосходило числа А. Цифра x — вторая цифра результата.
означает 10 * a + x) на x не превосходило числа А. Цифра x — вторая цифра результата.
4. Произведение числа 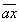 на x вычтем из числа A, припишем к найденной разности справа третью грань, получится некоторое число B. Удвоив имеющуюся часть результата, получим число b. Теперь подберем такую наибольшую цифру y, чтобы произведение числа
на x вычтем из числа A, припишем к найденной разности справа третью грань, получится некоторое число B. Удвоив имеющуюся часть результата, получим число b. Теперь подберем такую наибольшую цифру y, чтобы произведение числа 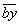 на y не превосходило числа B. Цифра y — третья цифра результата.
на y не превосходило числа B. Цифра y — третья цифра результата.
Следующий шаг правила повторяет 4-й шаг. Это продолжается до тех пор, пока не используется последняя грань.
Пример. Вычислить 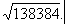
Решение. Разобьем число на грани: 13’83’84 — их три, значит, в результате должно получиться трехзначное число. Первая цифра результата 3, так как 3213, тогда как 4213. Вычтя 9 из 13, получим 4. Приписав к 4 следующую грань, получим A = 483. Удвоив имеющуюся часть результата, т. е. число 3, получим a = 6. Подберем теперь такую наибольшую цифру x, чтобы произведение двузначного числа 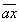 на x было меньше числа 483. Такой цифрой будет 7, так как 67 * 7 = 469 — это меньше 483, тогда как 68 * 8 = 544 — это больше 483. Итак, вторая цифра результата 7.
на x было меньше числа 483. Такой цифрой будет 7, так как 67 * 7 = 469 — это меньше 483, тогда как 68 * 8 = 544 — это больше 483. Итак, вторая цифра результата 7.
Вычтя 469 из 483, получим 14. Приписав к этому числу справа последнюю грань, получим b = 1484. Удвоив имеющуюся часть результата, т.е. число 37, получим B = 74. Подберем теперь такую наибольшую цифру y, чтобы произведение трехзначного числа 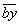 на y не превосходило 1484. Такой цифрой будет 2, так как 742 * 2 = 1484. Цифра 2 — последняя цифра результата. В ответе получили 372.
на y не превосходило 1484. Такой цифрой будет 2, так как 742 * 2 = 1484. Цифра 2 — последняя цифра результата. В ответе получили 372.
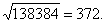
Если корень не извлекается, то после последней цифры заданного числа ставят запятую и образуют дальнейшие грани, каждая из которых имеет вид 00. В этом случае процесс извлечения корня бесконечен; он прекращается, когда достигается требуемая точность.
Реализовать набор подпрограмм для работы с длинными неотрицательными целыми числами (числами, выходящими за диапазон допустимых значений любого целого типа): 1) сложение; 2) вычитание; 3) умножение; 4) нахождение частного и остатка от деления одного числа на другое; 5) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
Длинное число представить следующим типом:
Type Tsifra = 0..9; Chislo = Array[1..1000] Of Tsifra;
Примечание. Набор подпрограмм можно реализовать в виде отдельного модуля.
Реализовать набор подпрограмм для работы с длинными произвольными целыми числами (числами, выходящими за диапазон допустимых значений любого целого типа): 1) сложение; 2) вычитание; 3) умножение; 4) нахождение частного и остатка от деления одного числа на другое; 5) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
Длинное число представить следующим типом:
Type Tsifra = 0..9; Chislo = Record Znak : 0..1; {0 — плюс, 1 — минус} Ch : Array [1..1000] Of Tsifra End;
Примечание. Набор подпрограмм можно реализовать в виде отдельного модуля.
Статьи к прочтению:
Артем Окулов: \
Похожие статьи:
-
ПОДГОТОВКА К ОЛИМПИАДАМ ПО ПРОГРАММИРОВАНИЮ В настоящее время олимпиады школьников по программированию, с одной стороны, продолжают пользоваться…
-
Формальные правила двоичной арифметики
Популярность двоичной системы счисления во многом определяется простотой выполнения арифметических действий: В основу арифметико-логического устройства…
