Функции и плотности распределения вероятностей случайных величин
Глава 2 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Дискретная случайная величина
1. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте и построить многоугольник полученного распределения.
2. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины X – числа нестандартных деталей среди четырёх отобранных и построить многоугольник полученного распределения.
3. Написать закон распределения случайной величины X – числа появлений «герба» при двух бросаниях монеты. Построить многоугольник полученного распределения.
4. Дискретная случайная величина X принимает три возможных значения: x1= — 4 с вероятностью p1=0,2; x2=6 с вероятностью p2=0,3; x3=10с вероятностью p3=0,5. Найти математическое ожидание данной случайной величины.
5. Дискретная случайная величина X принимает три возможных значения: x1=0,21 с вероятностью p1=0,1; x2=0,54 с вероятностью p2=0,5; x3=0,61с вероятностью p3=0,4. Найти математическое ожидание данной случайной величины.
6. Дискретная случайная величина X принимает три возможных значения: x1=4 с вероятностью p1=0,5; x2=6 с вероятностью p2=0,3и x3 с вероятностью p3. Найти x3 и p3, зная, что M(X)=8.
7. Найти дисперсию и среднее квадратичное отклонение дискретной величины X, заданной законом распределения:
| X | -5 | |||
| p | 0,4 | 0,3 | 0,1 | 0,2 |
8. Найти дисперсию и среднее квадратичное отклонение дискретной величины X, заданной законом распределения:
а)
| X | 4,3 | 5,1 | 10,6 |
| p | 0,2 | 0,3 | 0,5 |
б)
| X | ||||
| p | 0,05 | 0,10 | 0,25 | 0,60 |
9. Найти дисперсию дискретной случайной величины X – числа появлений события А в пяти независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,2.
10. Найти дисперсию дискретной случайной величины X – числа отказав элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.
11. Найти дисперсию дискретной случайной величины X – числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(X)=1,2.
12. Дискретная случайная величина X имеет только два возможных значения x1 и x2, причём x2x1. Вероятность того, что X примет значение x1, равна 0,6. Найти закон распределения величины X, если математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
13. Дискретная случайная величина X имеет только два возможных значения x1 и x2, причём x1
14. Дискретная случайная величина X имеет только три возможных значения x1=1, x2 и x3, причём x1
Функции и плотности распределения вероятностей случайных величин
1. Случайная величина X задана функцией распределения
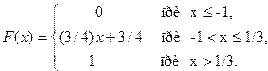
Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (0, 1/3).
2. Случайная величина X задана на всей оси Ox функцией распределения F(x) = 1/2 + (arctgx)/?. Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (0, 1).
3. Дана функция распределения непрерывной случайной величины X
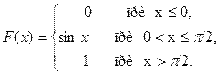
Найти плотность распределения f(x).
4. Дана функция распределения непрерывной случайной величины X
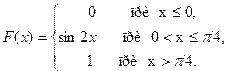
Найти плотность распределения f(x).
5. Случайная величина X задана функцией распределения
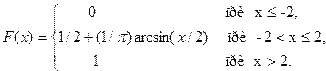
Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (-1, 1).
6. Случайная величина X задана функцией распределения
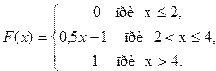
Найти вероятность того, что в результате испытания величина X примет значение: а) меньшее 0,2; б) меньшее трёх; в) не меньшее трёх; г) не меньшее пяти.
7. Случайная величина X задана функцией распределения
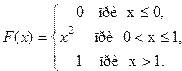
Найти вероятность того, что в результате четырёх независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу (0,25; 0,75).
8. Дискретная случайная величина X задана законом распределения
| X | |||
| p | 0,5 | 0,2 | 0,3 |
Найти функцию распределения F(x) и начертить её график.
9. Дискретная случайная величина X задана законом распределения
| X | ||||
| p | 0,2 | 0,1 | 0,4 | 0,3 |
Найти функцию распределения F(x) и начертить её график.
10. Непрерывная случайная величина X задана плотностью распределения f(x)=(3/2)sin3x в интервале (0; ?/3); вне этого интервала f(x)=0. Найти вероятность того, что X примет значение, принадлежащее интервалу (?/6; ?/4).
11. Задана плотность распределения непрерывной случайной величины X:
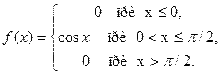
Найти функцию распределения F(x).
12. Задана плотность распределения непрерывной случайной величины X:
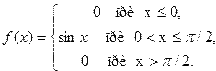
Найти функцию распределения F(x).
13. Задана плотность распределения непрерывной случайной величины X:
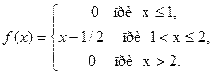
Найти функцию распределения F(x).
14. Задана плотность распределения непрерывной случайной величины X:
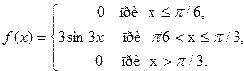
Найти функцию распределения F(x).
15. Случайная величина X задана на всей оси Ox функцией распределения F(x)=1/2+(1/?)arctg(x/2). Найти возможное значение x1, удовлетворяющее условию: с вероятностью 1/4 случайная величина X в результате испытания примет значение, большее x1.
Статьи к прочтению:
Физика — Плотность вещества
Похожие статьи:
-
Задача 4. плотность распределения случайной величины задана функцией
Итоговая контрольная работа Элементы теории вероятностей и математической статистики Вариант 1 Задача 1 В книжной лотерее разыгрывается пять книг. Всего…
-
Характеристика задержки и функция распределения электронов по энергиям
Вид характеристики задержки с параметрами установки t = 80 °С, =4В, представлен на рисунке 5.5. Как уже отмечалось выше, тот факт, что ток не падает до…
