Краткие теоретические сведения и методические указания к выполнению работы.

Метрики третьей группы базируются на оценке использования, конфигурации и размещения данных в программе. В первую очередь это касается глобальных переменных.

Предлагается метрика, связывающая сложность программ с обращениями к глобальным переменным.

Пара модуль — глобальная переменная обозначается как (p, r), где p — модуль, имеющий доступ к глобальной переменной r. В зависимости от наличия в программе реального обращения к переменной r формируются два типа пар модуль — глобальная переменная: фактические и возможные.

Возможное обращение к r с помощью p показывает, что область существования r включает в себя p.

Характеристика 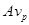говорит о том, сколько раз модули 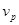действительно получали доступ к глобальным переменным, а число 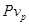– сколько раз они могли бы получать доступ.

Отношение числа фактических обращений к возможным определяется

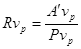. (9)

Эта формула показывает приближенную вероятность ссылки произвольного модуля на произвольную глобальную переменную.

Очевидно, чем выше эта вероятность, тем выше вероятность несанкционированного изменения какой-либо переменной, что может существенно осложнить работы, связанные с модификацией программы.

Покажем расчет метрики модуль – глобальная переменная . Пусть в программе имеются три глобальные переменные и три подпрограммы. Если предположить, что каждая подпрограмма имеет доступ к каждой из переменных, то мы получим девять возможных пар, т. е. 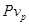= 9. Далее пусть первая программа обращается к одной переменной, вторая – к двум, а третья – не обращается ни к одной переменной. Тогда , .

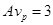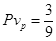Следующие две метрики сложности потока данных программ зарекомендовали себя с наилучшей стороны. Речь идет о спене и метрике Чепина.

Определение спена основывается на локализации обращений к данным внутри каждой программной секции. Спен – это число утверждений, содержащих данный идентификатор, между его первым и последним появлением в тексте программы. Следовательно, идентификатор, появившийся n раз имеет спен, равный .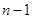

Что дает эта метрика? Предположим, мы обнаружили в программе идентификатор, спен которого равен 100. Тогда при построении трассы программы по этому идентификатору, по крайней мере, 100 контролирующих утверждений, что усложняет тестирование и отладку.

Следующей метрикой сложности потока данных программ является метрика Чепина. Существуют несколько её модификаций. Рассмотрим наиболее простой, а с точки зрения практического использования – достаточно эффективный вариант этой метрики.

Суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода.

Всё множество переменных, составляющих список ввода-вывода, разбивается на четыре функциональные группы:

1. Р – водимые переменные для расчетов и для обеспечения вывода. Примером может служить используемая в программах лексического анализатора переменная, содержащая строку исходного текста программы, то есть сама переменная не модифицируется, а только содержит исходную информацию.

2. М – модифицируемые или создаваемые внутри программы переменные.

3. С – переменные, участвующие в управлении работой программного модуля (управляющие переменные).

4. Т – не используемые в программе (паразитные) переменные.

Поскольку каждая переменная может выполнять одновременно несколько функций, необходимо учитывать её в каждой соответствующей функциональной группе.

Далее вводится значение метрики Чепина:

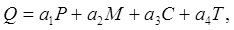(10)

где 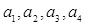– весовые коэффициенты.

Весовые коэффициенты в выражении (10) использованы для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики, наибольший вес, равный трём, имеет функциональная группа С, так как она влияет на поток управления программы. Весовые коэффициенты остальных групп распределяются следующим образом: 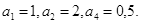Весовой коэффициент группы Т не равен нулю, поскольку паразитные переменные не увеличивают сложность потока данных программы, но иногда затрудняют её понимание. С учётом весовых коэффициентов выражение (10) принимает вид:

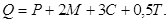(11)

Следует отметить, что рассмотренные метрики сложности программ основаны на анализе исходных текстов программ и графов программ, что обеспечивает единый подход к автоматизации их расчёта.

Метрика Кафура

Метрика такжеоснованная на учёте потока данных программы. Вводятся понятия локального и глобального потока:

Локальный поток информации из A в B существует, если:

Модуль А вызывает модуль В (прямой локальный поток)
Модуль В вызывает модуль А и А возвращает В значение, которое используется в В (непрямой локальный поток)
Модуль С вызывает модули А, В и передаёт результат выполнения модуля А в В

Глобальный поток информации из А в В через глобальную структуру данных D существует, если модуль А помещает информацию в D, а модуль В использует информацию из D. На основе этих понятий вводится величина I – информационная сложность процедуры:

I = length * (fan_in * fan_out)^2

Здесь:

length – сложность текста процедуры (меряется через какую-нибудь из метрик объёма, типа метрик Холстеда, Маккейба, LOC и т.п.)
fan_in – число локальных потоков внутрь процедуры плюс число структур данных, из которых процедура берёт информацию
fan_out – число локальных потоков из процедуры плюс число структур данных, которые обновляются процедурой

Можно определить информационную сложность модуля как сумму информационных сложностей входящих в него процедур. Следующий шаг – рассмотреть информационную сложность модуля относительно некоторой структуры данных. Информационная мера сложности модуля относительно структуры данных:

J = W * R + W * WrRd + WrRd x R + WrRd * (WrRd – 1)

Здесь:

W – число процедур, которые только обновляют структуру данных;
R – Только читают информацию из структуры данных;
WrRd – и читают, и обновляют информацию в структуре данных

Следующая метрика позволяет посчитатьоценку уровня комментированности программы F:

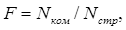(12)

где 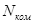– количество комментариев в программе; 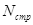– количество строк или операторов исходного текста.

Таким образом, метрика 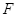отражает насыщенность программы комментариями.

Исходя из практического опыта, принято считать, что, 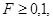то есть на каждые десять строк программы должен приходиться минимум один комментарий. Как показывают исследования, комментарии распределяются по тексту программы неравномерно: в начале программы их избыток, а в середине или конце – недостаток. Это объясняется тем, что в начале программы, как правило, расположены операторы описания идентификаторов, требующие более плотного комментирования. Кроме того, в начале программы также расположены шапки, содержащие общие сведения об исполнителе, характере, функциональном назначении программы и т.п. Такая насыщенность компенсирует недостаток комментариев в теле программы, и поэтому формула (12) недостаточно точно отражает комментированность функциональной части текста программы.

Более удачен вариант, когда вся программа разбивается на n равных сегментов и для каждого из них определяется :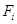

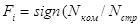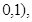– (13)

при этом:

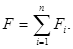(14)

Уровень комментированности программы считается нормальным, если выполняется условие: 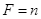. В противном случае какой-либо фрагмент программы дополняется комментариями до номинального уровня.

Следующая метрика Холстеда измеряет теоретическуюдлину программы 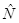используя аппроксимирующую формулу:

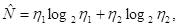(15)

где 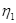– словарь операторов; 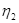– словарь операндов программы.

Вводя эту оценку, Холстед исходит из основных концепций теории информации, по аналогии, с которыми частота использования операторов и операндов в программе пропорциональна двоичному логарифму количества их типов. Таким образом, выражение (15) представляет собой идеализированную аппроксимацию (2), то есть справедливо для потенциально корректных программ, свободных от избыточности или несовершенств (стилистических ошибок). Несовершенствами можно считать следующие ситуации:

a) последующая операция уничтожает результаты предыдущей без их использования;

b) присутствуют тождественные выражения, решающие совершенно одинаковые задачи;

c) одной и той же переменной назначаются различные имена и т.п.

Подобные ситуации приводят к изменению 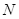без изменения .

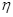Для стилистически корректных программ отклонение в оценке теоретической длины 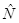от реальной N не превышает 10%.

Задание по работе

Оформить отчет по работе согласно заданному варианту, привести словесное описание алгоритма, приложить листинг программы с комментариями и выводы.

Вариант 1

Оценить сложность программы, используя метрику Кафура, основанную на учете потока данных программы.

Вариант 2

Оценить сложность программы, вычислив метрику, связывающую сложность программ с обращениями к глобальным переменным.

Вариант 3.

Оценить сложность программы, используя метрику сложности потока данных программ – спен.

Вариант 4

Оценить сложность программы, используя метрику сложности потока данныхпрограмм –метрику Чепина.

Вариант 5

Разработка программу оценки сложности ПО на базе отдельных метрик сложности программ— метрик стилистики, и понятности программ. Посчитатьоценку уровня комментированности программы F.

Вариант 6

Измерить теоретическуюдлину программы 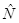,используя аппроксимирующую формулу.

Контрольные вопросы

1. Назвать метрики сложности программ, которые базируются на оценке использования конфигурации размещения данных в программе.

2. Дать определение метрики, связывающей сложность программы с обращениями к глобальным переменным.

3. Дать определение спена программы.

4. В чем состоит суть метрики Чепина?

5. Определить метрику Кафура, основанную на учете потока данных программы.

6. Какие программы являются потенциально корректными?

7. Какие ситуации в программе можно считать несовершенствами (стилистическими ошибками)?

8. Какой уровень комментированности программы принято считать достаточным?

9. Что такое теоретическая длина программы?

Краткие теоретические сведения и методические указания к выполнению работы.

Статьи к прочтению:

ФИЗИКА ЗА 5 МИНУТ — МЕХАНИКА

Похожие статьи: