Лабораторно-практическое занятие n4. умножение матриц. вычисление обратной матрицы. решение уравнений и систем линейных уравнений
Задание:научиться использовать программу Excel для решения задач линейной алгебры (вычисление определителей матрицы, умножение матриц, вычисление обратной матрицы, решение систем линейных уравнений), а также находить корни нелинейных уравнений.
Результат:пользовательсможет с помощью программы Excel находить корни уравнений и решать системы линейных уравнений, вычислять определители матрицы и использовать матричное исчисление для решения экономических задач.
Решение:
1. Загрузите программу Exсel.Переименуйте лист 1 (новое название листа — Матрицы).
2. Для решения задач, связанных с необходимостью умножения матриц, вычисления обратных матриц, вычисления определителей матрицы, используемых для решения систем линейных алгебраических уравнений в программе Excel предусмотрены соответствующие функции, расположенные в Мастере функций. Любая матрица представляет собой массив данных, представляемый в виде таблицы размера mx n с числовыми данными. Познакомимся с предоставляемыми возможностями программы Excelна примере решения следующих задач:
1) Даны две матрицы A и В:
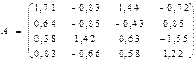
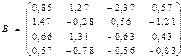
Необходимо:
a) вычислить определители матриц А и В;
б) найти матрицу, обратную к матрице А;
в) вычислить произведение матриц А и В.
г) осуществить проверку умножением прямой и обратной матриц, в результате должна получиться единичная матрица;
2) Решить систему линейных уравнений:
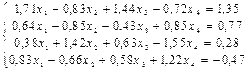
2.1. Для решения первой задачи в окне электронной таблицы введем элементы матриц А и В. В ячейке В1 введем заголовок — Матрица А, сами элементы матрицы расположим в ячейках А2:D5, каждое число — элемент матрицы вводится в отдельную ячейку. Соответственно в ячейке F1 введем заголовок — Матрица В, расположив ниже в ячейках F2:I5 элементы этой матрицы.
В ячейках А7 и F7 наберите заголовки: Определитель А=и Определитель В=.
Функция, используемая для вычисления определителя, имеет имя МОПРЕД, в качестве ее аргумента используется блок ячеек с элементами матрицы. В ячейку А8 введите формулу: МОПРЕД(А2:D5)и нажмите клавишу ввода Enter. В результате вы получите вычисленное значение определителя матрицы А. Аналогично в ячейке F8 вычисляется определитель матрицы В. Для ввода формулы можно использовать клавиатуру или Мастер функций.
2.2.Для вычисления матрицы А-1, обратной к матрице А, используется функция МОБР, аргументом которой является массив данных исходной матрицы А. Обратная матрица будет существовать, если определитель матрицы А # 0. В ячейку А10 введите заголовок: Обратная матрица. Поставьте курсор на ячейку А11 и выделите блок ячеек А11:D14. Войдите в Мастер функций и найдите функцию МОБР,в окне функции введите ее аргумент — А2:D5, нажмите кнопку Закончить (вы увидите набранную формулу в ячейке А11) установите текстовый курсор в строку формул и завершите ввод, нажавклавиши Shift+Ctrl+Enter. В результате в ячейках А11:D14 вы получите элементы обратной матрицы.
2.3. Для умножения матриц А и В используется функция МУМНОЖ,аргументами которой являются элементы этих матриц. При умножении двух матриц необходимо помнить, что число колонок 1-й матрицы должно равняться числу строк второй, т.е. если 1-я матрица имеет размер mxn, а 2-я матрица nxk, то в результате получится матрица размера mxk.
Введите в ячейку А16 заголовок — Результирующая матрица.Так как у нас матрицы А и В имеют размер 4х4, то в результате также будет матрица размера 4х4. Поставьте курсор в ячейку А17 и мышью выделите блок ячеек A17:D20. Вызовите Мастер функций и выберите функцию МУМНОЖ.В окне функции введите ее аргументы — блоки ячеек А2:D5и F2:I5и нажмите кнопку .В ячейке А17 вы увидите вводимую функцию. Для завершения ее ввода в блок ячеек установите текстовый курсор в строку формул и нажмите клавиши Shift+Ctrl+Enter.В результате в ячейках вы получите элементы результирующей матрицы- произведения матриц А и В.
2.4.Проверьте правильность вычисления обратной матрицы А-1умножением на нее исходной матрицы А, в результате должна получиться единичная матрица Е.
В ячейках, где представлены результаты, задайте числовой формат — два десятичных знака после запятой.
Умножение матриц часто используется при решении практических задач, где данные представлены в табличной форме.
