Логические элементы эвм. алгебра логики. законы алгебры логики.
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики или, как ее часто называют, булева алгебра.Основоположником этого раздела математики был Дж. Буль.
Булева алгебра оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые соответственно 1 и 0.
основной системой счисления ЭВМ является двоичная СС, в которой также используются только две цифры: 1 и 0. Таким образом, одни и те же цифровые устройства ЭВМ могут применяться для обработки как числовой информации в двоичной СС, так и логических переменных.
Совокупность значений логических переменных x1, x2, …, xn называется набором переменных.
Общее число ФАЛ n переменных определяется возведением числа 4 в степень n, т. е. 4n. Существуют четыре ФАЛ одной логической переменной.
Функции F0(х) = 0 и F3(х) = 1 являются константами (функции не изменяются при изменении аргумента). Функция F1(х) = х повторяет значение аргумента х. Функция F2(x) называется отрицанием переменной или инверсией и обозначается так:
F2(x) =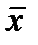 .
.
Из оставшихся десяти логических функций широкое распространение имеют функции F1(х) (конъюнкцияилилогическое умножение) и F7(х) (дизъюнкцияилилогическое сложение), которые совместно с функцией инверсии составляют функционально полную систему логических функций. С помощью этих трех функций можно представить (аналитически выразить) любую сколь угодно сложную логическую функцию. Очень важной для вычислительной техники является логическая функция исключающее ИЛИ (неравнозначность, сложение по модулю два). Функция исключающее ИЛИ обозначается символом A. Ниже приведены таблицы истинности для этих трех функций.
| Инверсия | |
| х | 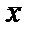 |
| x2 | x1 | x2 U x1 | x2 U x1 | x2A x1 |
Логические переменные, объединенные знаками логических операций, составляют логические выражения. При определении значения логического выражения принято следующее старшинство (приоритет) логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь — дизъюнкция. Для изменения указанного порядка используют скобки.
В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 0 и 1.
Кодирование информации. Кодовая таблица. Система кодирования ASCII. Система кодирования UNICODE.
Кодирование информации— это процесс формирования определенного представления информации.
все числа в компьютере представляются с помощью нулей и единиц (а не десяти цифр, как это привычно для людей). Иными словами, компьютеры обычно работают в двоичной системе счисления, поскольку при этом устройства для их обработки получаются значительно более простыми. Ввод чисел в компьютер и вывод их для чтения человеком может осуществляться в привычной десятичной форме, а все необходимые преобразования выполняют программы, работающие на компьютере.
Кодовая таблица
в кодовой таблице представлено определенное количество строк и только два столбца:
- в одном столбце указаны цифровые (в нашем случае двоичные) коды -слова, как сочетания элементов алфавита, расположенные в определенной последовательности;
- в другом столбце — их значения (нецифровой смысл, т. е. значения кодов).
Определение
Кодовая таблица — это совокупность цифровых (двоичных) кодов и их значений.
Самая распространенная система кодирования латиницы — ASCII — использует 7 бит на символ. Другие алфавиты обычно кодируются более сложным образом.Используются две основные кодировки латиницы — ASCII и EBCDIC (Extended Binary Coded Decimal Information Code), применяемая системами AS/400, System/370, System/390 и z90 фирмы IBM. Операции сравнения в современных процессорах реализованы как неразрушающее вычитание — мы производим те же действия, что и при обычном двоичном вычитании, но запоминаем не сам результат, а лишь флаги знака, переноса и равенства результата нулю. На основании значений этих флагов определяем результат сравнения: если разность равна нулю, сравниваемые символы одинаковы, если она положительна или отрицательна, один из символов больше или меньше другого.
В кодировке ASCII (American Standard Code for Information Interchange — Американский стандартный код обмена информацией), например, все символы латиницы, цифры и большинство распространенных знаков препинания обозначаются кодами от 0 до 127, при этом коды букв расставлены в соответствии с латинским алфавитом. В США, как и в других англоязычных странах, латинский алфавит используется в неизмененном виде, а для передачи звуков, отсутствовавших в оригинальном латинском языке, применяется причудливая орфография. Большинство других европейских алфавитов обходит проблему несоответствия фонетик путем расширения набора символов латиницы — например, в немецком языке добавлены буквы o, a, u и ?. Другие языки имеют множество различных акцентов и диакритических символов, расставляемых над буквами для указания особенностей произношения. Некоторые языки, например французский, используют одновременно и расширения алфавита, и причудливую орфографию. Нередко встречаются и дополнительные знаки препинания, например, ¿ и ¡ в испанском языке.
Все символы-расширения в каждом из национальных алфавитов находятся на определенных местах, но при использовании кодировки ASCII для представления этих символов сохранить этот порядок невозможно — соответствующие коды уже заняты. Так, в кодировке ISO 8895-1 все символы латиницы кодируются в соответствии с ASCII, а коды расширений более или менее произвольно раскиданы между 128 и 255. Более яркий пример той же проблемы — кодировки кириллицы семейства KOI, в которых символы кириллицы сопоставлены фонетически соответствующим им символам латиницы (филе нот фоунд, или, наоборот, esli wy не movete pro^itatx eto po-russki, smenite kodirovku). Естественно, совместить такое сопоставление и алфавитную сортировку невозможно.
Стандартным решением в таких случаях является использование для сравнения и лексикографической сортировки промежуточных таблиц, в которых для каждого допустимого кода указан его номер в лексикографическом порядке. На уровне системы команд процессоры этого обычно не делают, но на уровне библиотек языков высокого уровня это осуществляется очень часто.
Статьи к прочтению:
Элемент Музыка
Похожие статьи:
-
Базовыми операциями алгебры логики
операции логического умножения – конъюнкции ( ), логического сложения – дизъюнкции ( ), исключающего или – (A), логического отрицания – инверсии ( )….
-
Системы функций алгебры логики
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики. Теорема Жегалкина. Любая булева функция может быть представлена многочленом…
