Логическими элементами компьютеров являются электронные схемы и, или, не, и—не, или—не и другие (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.

Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

x	y	x . y

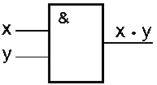
x	y	x v y

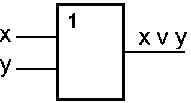
x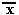

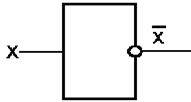
x	y

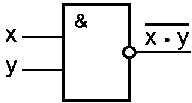
x	y

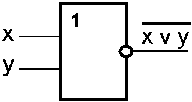
Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.

Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.

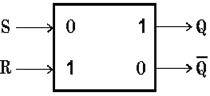Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс).

Он имеет два симметричных входа S и R и два симметричных выхода Q и 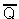, причем выходной сигнал Q является логическим отрицанием сигнала .

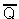На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( ).

При подаче единицы на вход S выходное состояние становится равным логической единице. А при подаче единицы на вход R выходное состояние становится равным логическому нулю.

Показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.

S	R	Q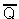
		запрещено


		хранение бита

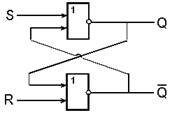
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ—НЕ .

Если на входы триггера подать S=“1”, R=“0”, то (независимо от состояния) на выходе Q верхнего вентиля появится “0”. После этого на входах нижнего вентиля окажется R=“0”, Q=“0” и выход 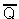станет равным “1”.
Точно так же при подаче “0” на вход S и “1” на вход R на выходе 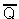появится “0”, а на Q — “1”.
Если на входы R и S подана логическая “1”, то состояние Q и 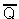не меняется.
Подача на оба входа R и S логического “0” может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора:

При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:

1. цифра ai первого слагаемого;

2. цифра bi второго слагаемого;

3. перенос pi–1 из младшего разряда.

В результате сложения получаются две цифры:

1. цифра ci для суммы;

2. перенос pi из данного разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:

Входы	Выходы
Первое слагаемое	Второе слагаемое	Перенос	Сумма	Перенос

Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.

Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0) может иметь вид:

40. ЛОГИЧЕСКИЕ ВЫСКАЗЫВАНИЕ. ВЫСКАЗЫВАТЕЛЬНАЯ ФОРМА. ЛОГИЧЕСКИЕ СВЯЗКИ. ТАВТОЛОГИЯ. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Что же такое логическое высказывание?

Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.

Так, например, предложение 6 — четное число следует считать высказыванием, так как оно истинное. Предложение Рим — столица Франции тоже высказывание, так как оно ложное.

Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения ученик десятого класса и информатика — интересный предмет. Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие интересный предмет. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.

Предложения типа в городе A более миллиона жителей, у него голубые глаза не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.

Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание площадь поверхности Индийского океана равна 75 млн кв. км в одной ситуации можно посчитать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.

Употребляемые в обычной речи слова и словосочетания не, и, или, если… , то, тогда и только тогда и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.

Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.

Так, например, из элементарных высказываний Петров — врач, Петров — шахматист при помощи связки и можно получить составное высказывание Петров — врач и шахматист, понимаемое как Петров — врач, хорошо играющий в шахматы.

При помощи связки или из этих же высказываний можно получить составное высказывание Петров — врач или шахматист, понимаемое в алгебре логики как Петров или врач, или шахматист, или и врач и шахматист одновременно.

Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.

Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание Тимур поедет летом на море, а через В — высказывание Тимур летом отправится в горы. Тогда составное высказывание Тимур летом побывает и на море, и в горах можно кратко записать как А и В. Здесь и — логическая связка, А, В — логические переменные, которые мoгут принимать только два значения — истина или ложь, обозначаемые, соответственно, 1 и 0.

Логическими элементами компьютеров являются электронные схемы и, или, не, и—не, или—не и другие (называемые также вентилями), а также триггер.

Статьи к прочтению:

Правда и мифы о мигрени и ее «сёстрах»| Лечение мигрени | Лечение головной боли

Похожие статьи: