Методика кодирования хаффмана

      Комментарии к записи Методика кодирования хаффмана отключены

Рассмотренная выше методика кодирования не всегда приводит к хорошему результату, вследствие отсутствия четких рекомендаций относительно того, как делить множество кодируемых знаков на подгруппы. Рассмотрим методику кодирования Хаффмана, которая свободна от этого недостатка.

Кодируемые знаки, также как при использовании метода Шеннона-Фано, располагают в порядке убывания их вероятностей (Таблица 3). Далее на каждом этапе две последние позиции списка заменяются одной и ей приписывают вероятность, равную сумме вероятностей заменяемых позиций. После этого производится пересортировка списка по убыванию вероятностей, с сохранением информации о том, какие именно знаки объединялись на каждом этапе. Процесс продолжается до тех пор, пока не останется единственная позиция с вероятностью, равной 1.

Таблица 3 — Код Хаффмана

Знаки pi Вспомогательные столбцы
Z1 0,22 0,22 0,22 0,26 0,32 0,42 0,58 0,1
Z2 0,2 0,2 0,2 0,22 0,26 0,32 0,42
Z3 0,16 0,16 0,16 0,2 0,22 0,26
Z4 0,16 0,16 0,16 0,16 0,2
Z5 0,1 0,1 0,16 0,16
Z6 0,1 0,1 0,1
Z7 0,04 0,06
Z8 0,02

После этого строится кодовое дерево. Корню дерева ставится в соответствие узел с вероятностью, равной 1. Далее каждому узлу приписываются два потомка с вероятностями, которые участвовали в формировании значения вероятности обрабатываемого узла. Так продолжают до достижения узлов, соответствующих вероятностям исходных знаков.

Процесс кодирования по кодовому дереву осуществляется следующим образом. Одной из ветвей, выходящей из каждого узла, например, с более высокой вероятностью, ставится в соответствие символ 1, а с меньшей – 0 (Рисунок 1). Спуск от корня к нужному знаку дает код этого знака. Правило кодирования в случае равных вероятностей оговаривается особо. Жирным шрифтом в таблице (Таблица 4) выделены объединяемые позиции, подчеркиванием – получаемые при объединении позиции.

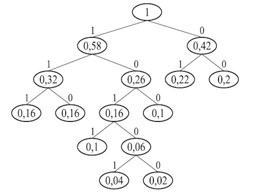
Рисунок 1 — Кодовое дерево

Таблица 4 — Код Хаффмана

Знаки Коды
Z1
Z2
Z3
Z4
Z5
Z6
Z7
Z8

Замечательным свойством кодов, построенных с применением методик Шеннона-Фано или Хаффмана, является их префиксность. Оно заключается в том, что ни одна комбинация кода не является началом другой, более длинной комбинации. Это позволяет при отсутствии ошибок осуществлять однозначное декодирование ряда следующих друг за другом кодовых комбинаций, между которыми отсутствуют разделительные символы.

Основным и, возможно, единственным существенным недостатком этого метода кодирования является то, что он кодирует символы с помощью целого количества бит, что снижает степень сжатия и уменьшает вероятность точного предсказание вероятностей.

Методы эффективного кодирования коррелированной

Последовательности знаков

Для повышения эффективности кодирования коррелированной последовательности искусственно производят декорреляцию. Один из способов заключается в укрупнении алфавита знаков. При этом передаваемые сообщения разбиваются на двух-, трех- или n – знаковые сочетания, вероятности которых известны. Каждое сочетание кодируется одним из описанных выше способов (Рисунок 2):

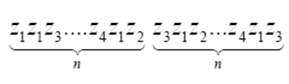
Рисунок 2 — Декорреляция

При увеличении числа знаков в сочетаниях корреляция знаков в сообщении уменьшается. Однако при этом возрастает задержка в передаче сигналов на время формирования сочетаний.

От этого недостатка в некоторой степени свободен метод, в котором каждое сочетание из l знаков (l – грамма) формируется путем добавления текущего знака сообщения и отбрасывания последнего знака l – граммы (Рисунок 3)

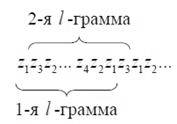
Рисунок 3 — Декорреляция после добавления знака

Сочетание из двух знаков называют диграммой, из трех – триграммой и т.д.

В процессе кодирования l – грамма непрерывно перемещается по тексту сообщения, а кодовое обозначение каждого знака сообщения зависит от l – 1 предшествующих знаков и может быть определено с использованием методик Шеннона – Фано или Хаффмана. Задержка сигнала в данном случае имеет место лишь на начальном этапе формирования первой l – граммы.

Недостатком такого метода заключается в том, что не учитываются корреляционные связи между знаками, входящими в состав следующих друг за другом сочетаний. Естественно, он проявляется тем меньше, чем больше знаков входит в каждое сочетание.

Статьи к прочтению:

Метод Хаффмана


Похожие статьи: