Методика проверки многомерных статистических гипотез

Статистические гипотезы – это выдвигаемые теоретические предположения относительно параметров статистического распределения или закона распределения случайной величины.

При проверке статистических гипотез используются понятия нулевой (прямой) и альтернативной (обратной) гипотез. Прямая гипотеза ( 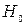) является основной и обычно содержит утверждение об отсутствии различий между сравниваемыми величинами. Альтернативная величина ( 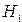) принимается после того, как отвергнута основная.

Для того чтобы проверить гипотезу, используют статистические критерии, позволяющие выяснить, следует ли принять или опровергнуть нулевую гипотезу. Если расчетное значение критерия не превышает критического, то есть веские основания для принятия прямой (нулевой) гипотезы. В противоположном случае целесообразно предположить справедливость альтернативной гипотезы ( ).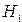

Проверка статистических гипотез всегда допускает определенную вероятность ошибки в выводах:

a – вероятность отвергнуть нулевую гипотезу, когда она справедлива;

b – вероятность принять нулевую гипотезу, когда она ложна.

В исследованиях обычно используется 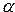, наиболее распространенными значениями которой в практике теории статистических решений являются: 0,01; 0,05; 0,1.

В соответствии с решаемой задачей различают параметрические (t-Стьюдента[5,6], F-Фишера[5,6]) и непараметрические гипотезы (Крамера-Уэлча [5,6], или Вилкоксона-Манна-Уитни [1,6]).

Основными алгоритмами проверки гипотез являются [1,6]:

— проверка гипотезы о равенстве вектора средних значений заданному вектору;

— проверка гипотезы о равенстве двух векторов средних значений.

Алгоритм проверки гипотезы о равенстве вектора средних значений заданному вектору. Известны 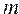выборочных средних, т.е. вектор средних значений: 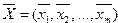. Вектор 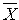сравнивается с заданным вектором 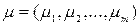. Прямая гипотеза имеет вид 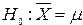, а альтернативная .

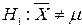Для проверки многомерной гипотезы данного вида используется Т-критерий Хотеллинга, рассчитываемый по следующей зависимости

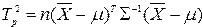, (1.1)

где 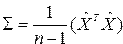– ковариационная матрица;

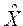– матрица с центрированными значениями .

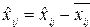Расчетное значение ( 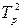) сравнивается с критическим значением, исчисляемым при заданном уровне ошибки первого рода 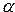и числе степеней свобода 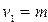и

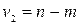
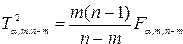. (1.2)

где 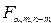– табличное значение F-критерия Фишера.

Многомерная гипотеза о равенстве вектора средних величин заданному вектору подтверждается при .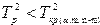

Пример 1. Для предприятия торговля в административном районе установлены следующие нормативные показатели эффективности деятельности – 20% и средняя продолжительность оборота средств – 12 дней. Результаты мониторинга коммерческой деятельности торговых предприятий района представлены в таблице 1.1.

Необходимо оценить существенность различий между фактическими значениями рассматриваемых показателей и установленными нормативами. Уровень 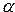= 0,05. Низкие значения уровня рентабельности и скорости оборота означают нарушение ритмичности товарно-денежных операций и снижение конкурентоспособности предприятий торговли.

Таблица 1.2 – Результаты мониторинга деятельности предприятий

Номер объекта	Рентабельность, %	Оборот средств, дней

Средн. значение ( 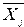)	15,8	17,8

Решение. Определить параметры многомерной случайной величины:

— вектор средних значений по столбцу ;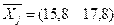

Фактическое значение 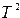— критерия Хотеллинга равно

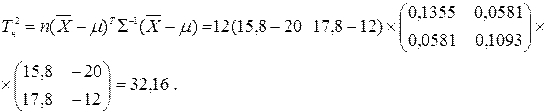
Критическое значение для заданного уровня значимости 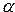= 0,05 составит

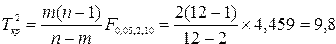Следовательно, расчетное значение 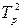критерия почти в три раза превосходит критическое (32,169,8), что свидетельствует о существенности расхождения между фактическими и нормативными значениями анализируемых показателей.

Проверка гипотезы о равенстве двух векторов средних значений. Проверяется гипотеза о равенстве векторов средних значений многомерных величин

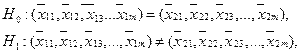
или в векторной форме 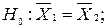и .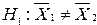

Для проверки данной гипотезы применяется многомерный 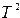-критерий, исчисляемый по формуле

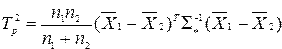, (1.3)

где 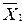, 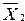— векторы средних значений;

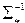— обратная матрица, рассчитанная для объединенной ковариационной матрицы

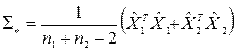где 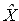— матрица центрированных значений .

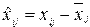Критические значения для 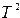находят по формуле

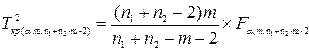. (1.4)

При 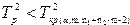нулевая гипотеза 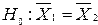принимается с вероятностью (1- 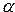). Если же 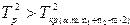, то нулевая гипотеза о равенстве векторов средних значений отвергается.

Пример. С целью анализа различий показателей производственно-хозяйственной деятельности родственных предприятий, расположенных в рамках свободной экономической зоны (первая группа) и за ее пределами (вторая группа), проведено выборочное обследование.

Из каждой группы предприятий сформированы две выборки неравных объемов. Результаты выборочного наблюдения представлены в таблице 1.2, в которой 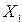— валовая добавленная стоимость на одного работника, тыс. ден. ед.; 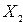— фондоотдача основных производственных фондов, ден. ед.

Таблица 1.3

Первая группа	Вторая группа
Номеробъекта		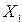	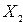Номеробъекта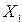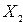
		3,25		2,90
		2,85		2,94
		2,90		3,00
		3,25		2,75
		4,90		3,30
		2,65		3,43
		4,00		2,80
		3,90
		5,24

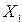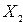По данным таблицы 1.2 следует оценить существенность различий двух групп предприятий по и при 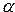= 0,01.

Решение. Для решения поставленной задачи проверяется гипотеза о равенстве векторов средних значений двух выборочных совокупностей.

1. Определение вектора средних значений и совместной ковариационной матрицы 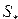, которые необходимы для расчета 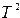-крите Хотеллинга

=( ); =( ),

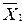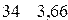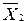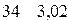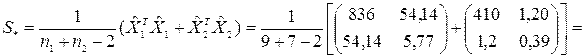
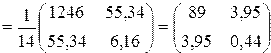отсюда, обратная матрица равна .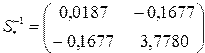

2. Расчет 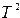-критерия Хотеллинга:

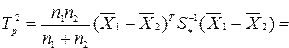
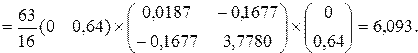
3. Критическое значение 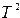-критерия имеет вид

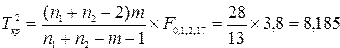Поскольку рассчитанное значение 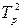= 6,093 меньше 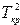= 8,185, нулевую гипотезу о равенстве векторов средних значений следует принять и сделать вывод о несущественном влиянии различных условий функционирования предприятий.

Статьи к прочтению:

Лекция 2: Проверка статистических гипотез

Похожие статьи: