Методы растрирования: антиэлайзинг, дизеринг.

Устранение ступенчатости (Antialiasing)

Одна из наиболее впечатляющих аппаратных технологий, все чаще находящая применение в игровых приложениях, — это устранение ступенчатости, или антиалиасинг (antialiasing).

Эта технология предназначена для устранения одной из ключевых проблем качества синтезированных изображений — лестничного эффекта (также часто называют алиасингом, aliasing). Часто этот эффект можно заметить на границах объектов или на линиях, близких к вертикальным или горизонтальным, но не строго вертикальных или, соответственно, горизонтальных. Несомненно, читатель много раз встречался с подобными эффектами, например, в трехмерных играх.

Рисунок 1. Левое изображение получено в стандартном режиме, правое — со включенным устранением ступенчатости. Обратите внимание на передачу мелких деталей и границы объектов (перила на мосту, фонари и т.д.)

Что является причиной лестничного эффекта? Опуская подробности, можно сказать, что главная причина — сетка пикселей на компьютерном мониторе. Эта сетка имеет конечное и весьма небольшое разрешение, а пиксели располагаются в строго фиксированных местах.

Ступенчатость возникает, когда точки на линиях пересекают строки или столбцы пикселей под небольшим углом. Часть линии шириной в один пиксель может попасть на один пиксель экрана, а часть — на другой. Таким образом, получается неопределенность: можно рисовать эту часть как один пиксель на одном ряду, один пиксель на другом ряду или закрашивать оба пикселя. К сожалению, все три способа вносят хорошо заметные дефекты в изображение. Если закрашивать только один пиксель, линия может получиться тоньше чем нужно, и будет хорошо заметен разрыв в том месте, где линия переходит с одного ряда пикселей на другой. Если закрашивать оба — ширина линии в этом месте будет два пикселя. Аналогичные артефакты возникают не только при рисовании линий, а практически на всех границах, встречающихся в изображении.

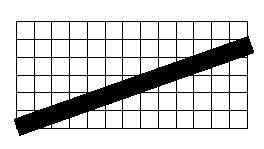
Рисунок 2.

Как же бороться с этим неприятным эффектом? Можно заметить, что размер одной ступеньки никогда не бывает больше, чем один пиксель. Поэтому наиболее естественный и простой путь — это увеличение экранного разрешения. То есть, увеличение разрешения уменьшает размер пикселя и, следовательно, заметность артефактов. Однако увеличить разрешение можно не всегда. Например, оно может быть ограничено максимальным разрешением монитора или его может ограничивать приложение.

Другой путь — увеличение так называемого эффективного разрешения, т.е. использование специального алгоритма для получения цвета пикселя таким образом, чтобы эмулировать несколько пикселей. Такие методы и называются методами устранения ступенчатости.

Эти методы вычисляют значение цвета как бы внутри экранного пикселя в нескольких точках. Эти точки называются сэмплами (sample). Сэмплы представляют собой те самые дополнительные пиксели изображения, которые увеличивают эффективное разрешение. Значение сэмплов используются для вычисления конечного цвета пикселя.

Дизеринг

Для иллюстрации работы реальных растровых устройств рассмотрим результаты вывода одной и той же картинки. Поскольку невозможно показать цветные изображения, то в качестве тестового образца выбран черно-белый рисунок, состоящий из текста и простейшей графики.

Изображение, полученное на экране, было сфотографировано и оцифровано. Картинка имеет множество градаций серого цвета, которые здесь, к сожалению, не могут быть точно воспроизведены. Для печати иллюстраций на бумаге (в том числе и для этой книги) используется дизеринг — имитация оттенков серого цвета многими близко расположенными черными точками. Поэтому при просмотре с помощью лупы данная картинка рассыпается на отдельные мелкие точки. На рис. 1.9 показано увеличенное изображение фрагмента рис. 1.8. Здесь уже отчетливо видна шестиугольная структура растра, характерная для цветного кинескопа.

Дизеринг

Хорошо, когда растровое устройство отображения может прямо воссоздавать тысячи цветов для каждого пиксела. Не так давно это было проблемой даже для компьютерных дисплеев (а точнее — для видеоадаптеров). Современные растровые дисплеи достаточно качественно отображают миллионы цветов, благодаря чему без проблем можно отображать цветные фотографии. Но для растровых устройств, которые печатают на бумаге, положение совсем другое. Устройства печати обычно имеют высокую разрешающую способность (dpi), часто на порядок большую, чем дисплеи. Однако нельзя непосредственно воссоздать даже сотню градаций серого для пикселов черно-белых фотографий, не говоря уже о миллионах цветов. В большинстве случаев можно увидеть, что оттенки цветов (для цветных изображений) или полутоновые градации (для черно-белых) имитируются комбинированием, смесью точек. Чем качественнее полиграфическое оборудование, тем меньше отдельные точки и расстояние между ними.

Для устройств печати на бумаге проблема количества красок достаточно важна. В полиграфии для цветных изображений обычно используют три цветных краски и одну черную, что в смеси дает восемь цветов (включая черный и белый цвет бумаги). Встречаются образцы печати большим количеством красок — например, карты, напечатанные с использованием восьми красок, однако такая технология печати намного сложнее. Состояние дел с цветной печатью можно оценить также на примере относительно простых офисных принтеров. Недавно появились струйные принтеры с шестью цветными красками вместо трех. В таких принтерах в состав обычных CMYK-красок добавлены бледно-голубая, бледно-пурпурная и бледно-желтая краски (семицветные принтеры). В шестицветных принтерах отсутствует бледно-желтая краска. Увеличение количества красок значительно улучшило качество печати, однако и этого пока явно мало.

Если графическое устройство не способно воссоздавать достаточное количество цветов, тогда используют растрирование — независимо от того, растровое это устройство или не растровое. В полиграфии растрирование известно давно. Оно использовалось несколько столетий тому назад для печати гравюр. В гравюрах изображение создается многими штрихами, причем полутоновые градации реализованы или штрихами различной толщины на одинаковом расстоянии, или штрихами одинаковой толщины с переменной густотою расположения. Такие способы используют особенности человеческого зрения и в первую очередь — пространственную интеграцию. Если достаточно близко расположить маленькие точки различных цветов, то они будут восприниматься как одна точка с некоторым усредненным цветом. Если на плоскости густо расположить много маленьких разноцветных точек, то будет создана визуальная иллюзия закрашивания плоскости некоторым усредненным цветом. Однако если увеличивать размеры точек и (или) расстояние между ними, то иллюзия сплошного закрашивания исчезает — включается другая система человеческого зрения, обеспечивающая нашу способность различать отдельные объекты, подчеркивать контуры.

В компьютерных графических системах часто используют эти методы. Они позволяют увеличить количество оттенков цветов за счет снижения пространственного разрешения растрового изображения. Иначе говоря— это обмен разрешающей способности на количество цветов. В литературе по компьютерной графике такие методы растрирования получили название dithering (дрожание, разрежение).

Простейшим вариантом дизеринга можно считать создание оттенка цвета парами соседних пикселов.

Если рассмотреть ячейки из двух пикселов (рис. 1.36), то ячейка номер 1 дает оттенок цвета

С = (С1+С2)/2,

где С1 и С2 — цвета, которые графическое устройство способно непосредственно воспроизвести для каждого пиксела. Числовые значения С, С1 и С2 можно рассчитать в полутоновых градациях или в модели RGB — отдельно для каждой компоненты.

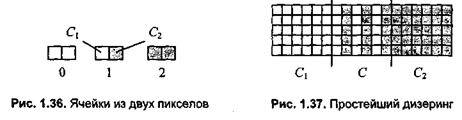
Пример растра с использованием ячеек из двух пикселов приведен на рис. 1.37.

Как видим, для создания промежуточного оттенка С ячейки образовывают вертикальные линии, которые очень заметны. Для того чтобы человек воспринял это как сплошной оттенок, необходимо, чтобы угловой размер ячеек был меньше одной угловой минуты. Можно изменять положения таких ячеек в растре, располагая их, например, по диагонали. Это несколько лучше, но не намного.

Чаще используют квадратные ячейки больших размеров. Дадим пример ячеек размером 2*2 (рис. 1.38).

Такие ячейки дают 5 градаций, из них три комбинации (1, 2, 3) образуют новые оттенки.

Расчет цвета, соответствующего одной из комбинаций пикселов в ячейке, можно выполнить таким образом. Если пикселы ячейки могут быть только двух цветов (С1 и С2), то необходимо подсчитать часть площади ячейки для пикселов каждого цвета. Цвет ячейки (С) можно оценить соотношением

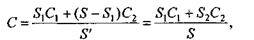
где S — общая площадь ячейки; S1 u S2 — части площади, занятых пикселами цветов C1 и С2 соответственно, причем S1 + S2 = S. Проще всего, когда пикселы квадратные, а их размер равен шагу размещения пикселов. Примем площадь одного пиксела за единицу. В этом случае площадь, занимаемая пикселами в ячейке, равна их количеству (рис. 1.41).

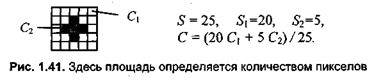
Для ячейки 5

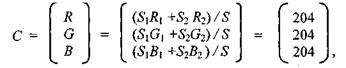Еще пример. Если С1 — желтый (RGB) = (255, 255, 0), а С2— красный (RGB) = (255, 0, 0), то С = (255, 204, 0). Это оттенок оранжевого цвета.

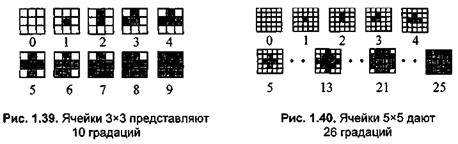
Следовательно, если в ячейке размерами n*n использованы два цвета, то с помощью этой ячейки можно получить п2+1 различных цветовых градаций. Две комбинации пикселов — когда все пикселы ячейки имеют цвет С1 или С2 — дают цвет ячейки соответственно С1 или С2. Все иные комбинации дают оттенки, промежуточные между С1 и С2.

Можно считать, что ячейки размером п х п образовывают растр с разрешающей способностью в п раз меньшей, чем у исходного растра, а глубина цвета возрастает пропорционально п2. Для характеристики изображений, которые создаются методом дизеринга, используют термин линиатура растра. Линиатура вычисляется как количество линий (ячеек) на единицу длины — сантиметр, миллиметр, дюйм. В последнем случае единицей измерения для линиатуры является Ipi (по аналогии с dpi).

Для дизеринга используют квадратное и диагональное расположение ячеек.

Для примера квадратного изображения специально была выбрана небольшая разрешающая способность, чтобы подчеркнуть структуру изображения. Ячейки образовывают достаточно заметный квадратный растр (рис. 1.42).

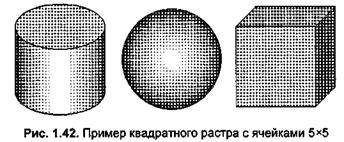
Для улучшения восприятия изображения можно использовать иное расположение ячеек, например, диагональное (рис 1.43).

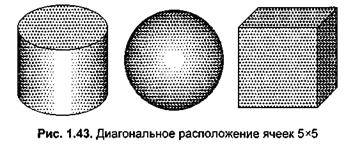
Диагональное расположение можно получить, если сдвигать четные строки ячеек (рис. 1.44). Координаты пикселов ячеек можно вычислять следующим образом:

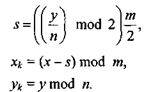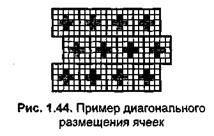
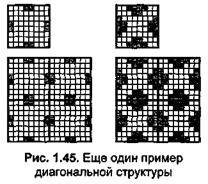
Для того чтобы получить диагональную структуру растра подобную той, что используется для печати газет, можно использовать квадратное расположение ячеек другого типа (рис. 1.45).

Для всех приведенных выше примеров дизеринга ячейки образовывают точки переменного размера с постоянным шагом. Однако часто используется иной подход— переменная густота расположения точек постоянного размера. Такой способ получил название частотной модуляции (ЧМ) (рис. 1.46).

Положительная черта способа ЧМ — меньшая заметность структуры растра. Однако его использование затруднено в случае, когда размер пикселов больше, чем их шаг. Начиная с определенной густоты, пикселы смыкаются. Кроме того, на дискретном растре невозможно обеспечить плавное изменение густоты (частоты), в особенности для ячеек небольшого размера. Рассмотрим пример ячеек 5 х5, реализующих ЧМ-дизеринг (рис. 1.47).

Для изображений, созданных методом ЧМ-дизеринга, наблюдается меньшая заметность растровой структуры (рис. 1.48).

Однако при регулярном расположении одинаковых ячеек всегда образовывается текстура, муар, лишние контуры. Одна из важных задач — разработка таких вариантов ячеек, которые предопределяют наименее заметную растровую структуру (кроме тех случаев, когда, наоборот, такую структуру нужно подчеркнуть для создания изображения в стиле гравюры). Это довольно сложная задача.

Один из способов создания достаточно качественных изображений — это диффузный дизеринг. Суть его в том, что ячейки создаются случайно (или псевдослучайно). Если для каждой градации создавать случайные ячейки, то даже для фрагмента растра пикселов с постоянным цветом не будут образовываться регулярные структуры. Это соответствует диффузному отражению света от матовой поверхности.

Статьи к прочтению:

История появления крутого графена в играх. SSAO и Antialiasing

Похожие статьи: