Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.
Запись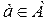 
означает, что элемент а принадлежит множеству А. Запись 
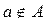— наоборот, Что элемент а множеству А не принадлежит. Знак 
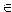называют знаком принадлежности.
Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.
Например: {2, 4, 6} = {4, 2, 6} – равные множества.
Определение 2. Множество называется непустым, если содержит хотя бы один элемент.
Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
В этом случае пишут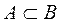 
, знак 
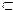называют знаком включения.
Например: {2, 4,} 
{4, 2, 6}
Рассмотрим свойства отношения включения.
рефлексивно, т.е любое множество является подмножеством самому себе.
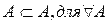
транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.
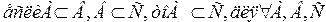
антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.
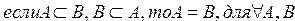
Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.
Пустое множество обозначают 
Пустое множество является подмножеством любого множества.
Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).
В дальнейшем будем пользоваться следующим утверждением:
Утверждение 1. Число всех подмножеств конечного множества равно 2n.
Пример. Выделим все подмножества множества А ={2, 4, 6}.
Р(А)={2, 4, 6}, {2, 4}, {4, 6}, {2, 6}, {2}, {4 }, {6}, 
— всего 23=8.
Операции над множествами
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.
Для обозначения объединения множеств используют знак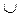 
.
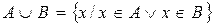
Пример. 
, 
, 
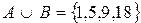
Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.
Для обозначения пересечения множеств используют знак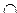 
.
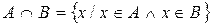
Пример. , , 
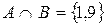
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.
Для обозначения разности множеств используют знак /.
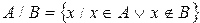
Пример. , , 
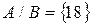
Перечислим основные свойства операций над множествами:
1) 
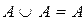идемпотентность объединения
2) 
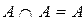идемпотентность пересечения
3) 
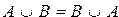коммутативность объединения
4) 
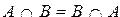коммутативность пересечения
5) 
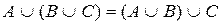ассоциативность объединения
6) 
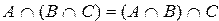ассоциативность пересечения
7) 
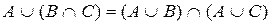дистрибутивность объединения относительно пересечения
8) 
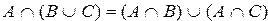дистрибутивность пересечения относительно объединения
Универсальное множество. Дополнение множества.
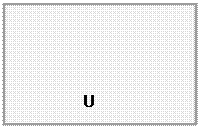
Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.
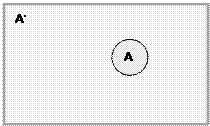
Определение 6. Множество U/А называется дополнением множества А и обозначается 
(или 
).
Дополнение U/ множества обозначается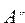 
Справедливы следующие формулы: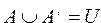 
= 
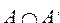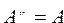— закон инволюции.
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.
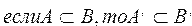
Доказательство.
Пусть множество А является подмножеством множества В,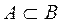 
, необходимо доказать, что для каждого элемента х из универсального множества U выполняется следующее условие: если элемент х принадлежит множеству 
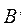, то он принадлежит и множеству .
.
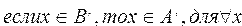Действительно, если х принадлежит множеству 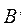, то он не принадлежит множеству В, а т. к. множество А является подмножеством множества В, то элемент х не принадлежит и множеству А, а это означает его принадлежность множеству .
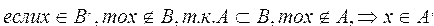
Теорема. Имеют место следующие тождества
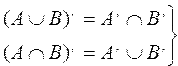— Законы де Моргана для множеств
Приведем краткое доказательство первого утверждения.
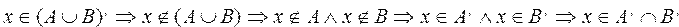Второе утверждение докажите самостоятельно.
Диаграммы Эйлера-Венна.
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.
Объединение множеств Пересечение множеств
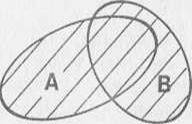
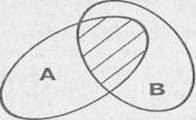
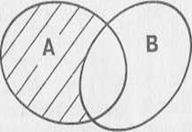
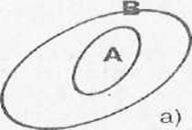
Разность множеств Подмножество
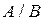
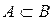
Универсальное множество Дополнение
 |  |