Обработка структурированных данных в scilab
Краткие теоретические сведения
В Scilab можно использовать различные типы структурированных данных, т.е. данных, содержащих несколько элементов. К основным структурированным данным относятся массивы чисел (вектора, матрицы, многомерные массивы).
Массив — это последовательность однотипных элементов, снабженных индексами (порядковыми номерами). Вектором принято называть одномерный массив. Матрица — это двумерный массив. Векторы в Scilab делятся на векторы-строки и векторы-столбцы.
Занести числа в вектор можно несколькими способами.
1) Непосредственный ввод
Чтобы задать вектор-строку, значения его элементов следует перечислить в квадратных скобках, разделяя пробелами.
Например,
V=[ 2 3 8 0 ]
Чтобы задать вектор-столбец, значения его элементов следует перечислить в квадратных скобках, используя для разграничения строк точку с запятой.
V=[2;3;8]
Обращение к элементу вектора выполняется указанием имени вектора и номера элемента в векторе в круглых скобках.
Например, V(2) a 3
V(3) a 8
2) Ввод с использованием диапазона
Общий вид диапазона:
xn : dx : xk
xn – начальное значение диапазона;
dx – шаг изменения значений диапазона;
xk – конечное значение диапазона;
Для формирования вектора следует задать:
X=xn:dx:xk
В результате будет сформирован вектор, первый элемент которого равен xn, второй – xn+dx, третий — xn+dx+dx и т.д. Последний элемент будет не больше xk для положительного шага dx , и не меньше xk – для отрицательного. Если величина шага отсутствует, то по умолчанию его значение равно 1 или -1, тогда вид диапазона таков:
X=xn: xk
Примеры правильной записи задания вектора с использованием диапазонов приведены ниже.
| Фрагмент программыa=5:2:15disp(a)v=3:5disp(v) | Командное окно5 7 9 11 13 153 4 5 |
Задачу о табулировании функции можно решить с помощью формирования векторов X и Y, например:
X=0:0.5:6.28
Y=cos(X)
В этом случае в каждый элемент вектора Y поместится косинус от каждого элемента вектора Х.
Чтобы задать матрицу, значения ее элементов следует перечислить в квадратных скобках, разделяя элементы в строках пробелами или запятыми, а для разграничения строк использовать точку с запятой.
Например,
| Фрагмент программыA=[ 3 1 -3; 2 0 1.5] | Командное окно3. 1. -3.2. 0 1.5 |
Для указания отдельного элемента матрицы после имени матрицы в круглых скобках указываются два индекса: номер строки и номер столбца.
Например, M(2,3) – это второй по строке и третий по столбцу элемент матрицы M.
Система имеет обширный набор стандартных функций и операций по обработке матриц, который позволяет:
— формировать новые матрицы стандартного вида;
— выполнять матричные арифметические операции;
— вычислять матричные характеристики и математические функции.
Для формирования новых матриц стандартного вида применяются следующие системные функции:
rand(M,N) – формирует прямоугольную матрицу размерностью M?N, элементами которой являются случайные числа в интервале (0.0; 1.0), функция rand без параметров формирует одно случайное число в том же интервале.
ones(M,N) формирует матрицу размерностью M?N, состоящую из единиц.
zeros(M,N) формирует матрицу размерностью M?N, состоящую из нулей.
diag(V) создает диагональную матрицу, в которой элементы вектора V являются элементами главной диагонали.
Матричные арифметические операции представлены следующими:
A+B , A-B матричное сложение и вычитание. Оба операнда этой операции должны иметь одинаковую размерность, если они являются матрицами. Один из операндов может выть скалярной величиной.
A*B матричное умножение. Операция выполняется по правилам матричного умножения, число столбцов матрицы A должно быть равно числу строк матрицы B.
Х ^ Р возведение матрицы в степень. Эта операция при скалярном значении Р возводит квадратную матрицу Х в степень Р. Если Х – скалярная величина, а Р – квадратная матрица, то Х^Р возводит Х в матричную степень Р. Эта операция является ошибочной, если оба операнда – матрицы.
В Scilab существуют матричные операции, которые выполняются над каждым элементом матрицы, это такие операции, как:
.* поэлементное матричное умножение.
.\поэлементное левое деление матриц.
. / поэлементное правое деление матриц.
.^поэлементное возведение матрицы в степень.
Оба операнда этих операций должны иметь одинаковую размерность, или один из них должен являться скалярной величиной.
Операция «апостраф» ? вычисляет транспонированную матрицу.
Ниже приведены примеры выполнения матричных арифметических операций.
| Фрагмент программы умножения двух матрицx=[2 3 4; 5 6 7]y=[9 8; 7 6; 5 4]z=x*ydisp(z) | Командное окно59 50122 104 |
| Фрагмент программы умножения матрицы на вектор x=[2 3 4; 5 6 7]t=[3; 6; 9]z=x*tdisp(z) | Командное окно |
| Поэлементное умножение двух матриц x=[2 3 4; 5 6 7]y=[9 8 7 ; 6 5 4]z=x .*ydisp(z) | Командное окно18 24 2830 30 28 |
| Вычисление транспонированной матрицыy=[9 8 7 ; 6 5 4]w=y’disp(w) | Командное окно9 68 57 4 |
Система содержит стандартные функции, позволяющие вычислять различные характеристики матриц:
det(A) вычисляет определитель матрицы;
trace(A) вычисление следа матрицы;
rank(A) вычисление ранга матрицы;
inv(A) вычисление обратной матрицы.
Ниже приведены примеры вычисления этих характеристик для матриц А и В.
| Фрагмент программы вычисления определителя матрицыx=[2 3 4; 5 6 7; 1 2 2];d=det(x)disp(“определитель =”)disp (d) | Командное окноопределитель = |
| Фрагмент программы вычисления обратной матрицыx=[2 3 4; 5 6 7; 1 2 2];Z= inv(x)disp(Z) | Командное окно-0.6667 0.6667 -1.-1. 0 2.1.3333 -0.3333 -1. |
Над массивами можно выполнять различные операции, заданные системными функциями.
max(А) — вычисление максимального элемента массива;
min(А) — вычисление минимального элемента массива;
sum(A) — вычисление суммы элементов массива;
prod(A) — вычисление произведения элементов массива;
mean(A) — вычисление среднего значения элементов массива.
[Amax, Nmax]= max(A) — вычисление максимального элемента в массиве и его номера. Порядок применения этих функций и результаты их выполнения рассмотрены на примерах.
| Поиск максимального значения матрицы и номера его строки и столбцаy=[2 3 4; 55 6 7; 1 12 2];[ymax,nmax]=max(y)disp(y)disp(ymax)disp(nmax) | Командное окно2. 3. 4.55. 6. 7.1. 12. 2.55.2. 1. | |
| Фрагмент программы вычисления суммы элементов матрицыx=[2 3 4; 5 6 7; 1 2 2];s=sum(x), disp(s) | Командное окно | |
Практическая часть
Задание 1. Создание нескольких векторов с указанными параметрами
Постановка задачи. Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1.
Создать вектор d, значения которого изменяются от 2 до 7 с шагом 0,5.
Пример программы по выполнению этого задания приведен ниже.
| Программа | Результаты расчетов |
| x=22:37disp(вектор х)disp(x)d=2:0.5:7disp(вектор d)disp(d) | вектор х22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37.вектор d2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. |
Индивидуальные задания приведены в таблице 2.2.
Таблица 2.2
| № | Задание |
| Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1.Создать вектор d, значения которого изменяются от 2 до 7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 32 до 43 с шагом 1.Создать вектор y, значения которого изменяются от 12 до 27 с шагом 0,2. | |
| Создать вектор х, значения которого изменяются от 3 до 13 с шагом 1.Создать вектор q, значения которого изменяются от 1,2 до 2,7 с шагом 0,05. | |
| Создать вектор х, значения которого изменяются от 15 до 26 с шагом 1.Создать вектор b, значения которого изменяются от 18,2 до 23,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 9 до 18 с шагом 1.Создать вектор u, значения которого изменяются от 6,2 до 13,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 42 до 57 с шагом 1.Создать вектор r, значения которого изменяются от 16,2 до 30,7 с шагом 0,5. | |
| Создать вектор a, значения которого изменяются от 17 до 32 с шагом 1.Создать вектор w, значения которого изменяются от 26,7 до 44,2 с шагом 0,8. | |
| Создать вектор х, значения которого изменяются от 32 до 47 с шагом 1.Создать вектор d, значения которого изменяются от 12 до 17 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 23 до 40 с шагом 1.Создать вектор y, значения которого изменяются от 2 до 17 с шагом 1,2. | |
| Создать вектор х, значения которого изменяются от 8 до 23 с шагом 1.Создать вектор q, значения которого изменяются от 13,2 до 22,7 с шагом 0,9. | |
| Создать вектор х, значения которого изменяются от 25 до 36 с шагом 1.Создать вектор b, значения которого изменяются от 8,2 до 13,7 с шагом 0,5. | |
| Создать вектор х, значения которого изменяются от 19 до 38 с шагом 1.Создать вектор u, значения которого изменяются от 16,2 до 23,7 с шагом 0,7. | |
| Создать вектор х, значения которого изменяются от 22 до 37 с шагом 1.Создать вектор r, значения которого изменяются от 26,2 до 43,7 с шагом 0,5. | |
| Создать вектор a, значения которого изменяются от 27 до 39 с шагом 1.Создать вектор w, значения которого изменяются от 22,7 до 40,2 с шагом 0,9. | |
| Создать вектор a, значения которого изменяются от 17 до 41 с шагом 1.Создать вектор w, значения которого изменяются от 16,7 до 34,2 с шагом 0,6. |
Задание 2.Создание одномерного массива как диапазона с заданными пределами изменения
Постановка задачи. Создать одномерный массив как диапазон с заданными пределами изменения. Массив должен содержать не менее 10 чисел. Сформировать новый одномерный массив, содержащий значения функции от элементов исходного массива.
| Функция | хн | хк |
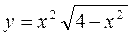 |
Для выполнения этого задания запрограммируем следующие действия:
Шаг 1. Создадим вектор x, значения которого будут изменяться от 0 до 2 с шагом 0.2 (вектор создается с использованием диапазона).
Шаг 2. Создадим вектор y, каждое значение которого вычисляется с помощью заданной формулы (не забываем про поэлементные операции над векторами).
Шаг 3. Выведем в командное окно числовые значения полученных векторов.
| Программа | Результаты расчетов |
| clearx=0:0.2:2y=(4-x^2).*x^2disp(вектор x)disp(x)disp(вектор y)disp(y) | вектор x0. 0.2 0.4 0.6 0.8 1. 1.2 1.4 1.6 1.8 2.вектор y0. 0.1584 0.6144 1.3104 2.1504 3. 3.6864 3.9984 3.6864 2.4624 0. |
Индивидуальные задания приведены в таблице 2.3.
Таблица 2.3
| №вар. | Функция | X1 | X2 | №вар. | Функция | X1 | X2 |
| 1. | 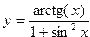 | 2. | 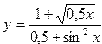 | ||||
| 3. | 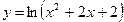 | -3 | 4. | 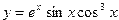 | -1 | ||
| 5. | 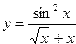 | 6. | 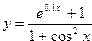 | ||||
| 7. | 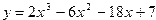 | -2 | 8. | 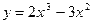 | |||
| 9. | 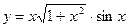 | 10. | 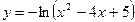 | ||||
| 11. | 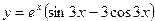 | 12. | 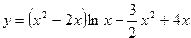 | ||||
| 13. | 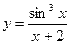 | 14. | 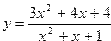 | -1 | |||
| 15. | 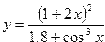 | 16. | 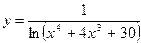 | -1 |
Задание 3. Обработка матриц и векторов
Постановка задачи. Даны две матрицы А и В.
A= 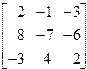 B= B= 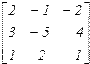 |
1) Создать вектор V1 из второго столбца матрицы А, вектор V2 из третьей строки матрицы В и вектор V3 из первого столбца матрицы B.
Порядок составления программы таков.
Шаг 1. Создаем матрицы перечислением элементов по строкам, разделителем между строками является «;».
Шаг 2. Выводим матрицы в командное окно.
Шаг 3. Формируем вектор V1 из всех строк второго столбца матрицы A, поэтому в качестве номера строки матрицы указываем символ «:», что означает «все», а в качестве номера столбца указываем 2. Аналогично формируются вектора V2 и V3;
Шаг 4. Выводим значения векторов в командное окно.
| Программа | Результаты расчетов |
| A=[2 -1 -3; 8 -7 -6; -3 4 2]B=[2 -1 -2; 3 -5 4; 1 2 1]disp(A)disp(B) | 2. — 1. — 3.8. — 7. — 6.- 3. 4. 2.2. — 1. — 2.3. — 5. 4.1. 2. 1. |
| V1=A(:,2)V2=B(3,:)V3=B(:,1)disp(V1)disp(V2)disp(V3) | — 1.- 7.4.1. 2. 1.2.3.1. |
2) Вычислить V2?V1 и A?V1.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, R1 и R2, которые будут являться результатами выполнения операций умножения.
Шаг 2. Так как операции умножения выполняются по законам математики, то точка перед знаком умножения не ставится. Ожидаемый результат умножения двух векторов – одно число, а результат умножения матрицы на вектор – это вектор-столбец из трех элементов.
Шаг 3. Выводим результаты в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| R1=V2*V1disp(R1)R2=A*V1disp(R2) | — 11.- 7.17.- 17. |
3) Вычислить A?B, A-1, BT.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, W1, W2, W3, которые будут являться результатами выполнения операций.
Шаг 2. Так как операции умножения матриц выполняются по законам математики, то точка перед знаком умножения не ставится. Ожидаемый результат умножения двух матриц – матрица из трех строк и трех столбцов.
Шаг 3. Вычисляем обратную матрицу с помощью стандартной функции inv, выводим результат в командную область с помощью оператора disp.
Шаг 4. Вычисляем транспонированную матрицу матрицу с помощью стандартной операции «апостраф» — B’, выводим результат в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| W1=A*Bdisp(W1)W2=inv(A)disp(W2)W3=B’disp(W3) | — 2. — 3. — 11.- 11. 15. — 50.8. — 13. 24.- 0.6666667 0.6666667 1.- 0.1333333 0.3333333 0.8- 0.7333333 0.3333333 0.42. 3. 1.- 1. — 5. 2.- 2. 4. 1. |
4) Вычислить определители А и В.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, S1, S2, которые будут являться результатами выполнения операций.
Шаг 2. Определители матриц вычисляем в программе с помощью стандартной функции det. Выводим результат в командную область с помощью оператора disp.
| Программа | Результаты расчетов |
| S1=det(A)S2=det(B)disp(S1)disp(S2) | — 15.- 49. |
5) Вычислить вектор V3 поэлементным умножением векторов V1 и V3.
6) Вычислить матрицу D поэлементным умножением матриц A и B.
Порядок составления программы таков.
Шаг 1. Выбираем переменные, например, Z1, Z2, которые будут являться результатами выполнения операций.
Шаг 2. Так как операция умножения двух векторов выполняется поэлементно, то перед знаком умножения ставится точка. Ожидаемый результат поэлементного умножения двух векторов – вектор из трех элементов.
Шаг 3. Так как операция умножения двух матриц выполняется поэлементно, то перед знаком умножения ставится точка. Ожидаемый результат поэлементного умножения двух матриц – матрица из трех строк и трех столбцов.
| Программа | Результаты расчетов |
| Z1=V1.*V3disp(Z1) Z2=A.*Bdisp(Z2) | — 2.- 21.4.4. 1. 6.24. 35. — 24.- 3. 8. 2. |
Индивидуальные варианты приведены в таблице 2.4.
Таблица 2.4.
| 1. | A= 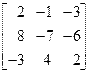 B= B= 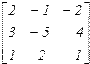 | 2. | A= 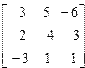 B= B= 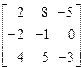 |
| 3. | A=  B= B= 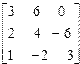 | 4. | A= 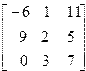 B= B= 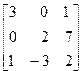 |
| 5. | A= 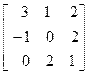 B= B= 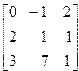 | 6. | A=  B= B= 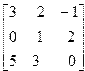 |
| 7. | A= 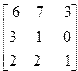 B= B= 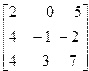 | 8. | A= 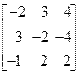 B= B= 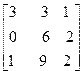 |
| 9. | A= 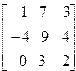 B= B= 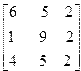 | 10. | A=  B= B= 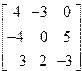 |
| 11. | A= 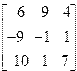 B= B= 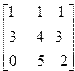 | 12. | A=  B= B= 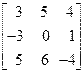 |
| 13. | A= 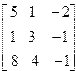 B= B= 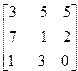 | 14. | A= 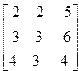 B= B= 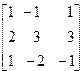 |
| 15. | A=  B= B= 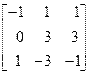 | 16. | A=  B= B=  |
Задание 4. Вычисление суммы и произведения
Постановка задачи. Вычислить сумму и произведение элементов по заданным формулам.
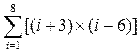 | 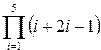 |
Порядок составления программы таков.
Шаг 1. Создаем вектор, который будет изменяться от нижнего предела суммирования до верхнего, например, от 1 до 8.
Шаг 2. Создаем вектор F, каждый элемент которого вычисляется по формуле, стоящей под знаком суммирования.
Шаг 3. Находим сумму элементов этого вектора с помощью стандартной функции sum, результат помещаем в переменную SS и выводим ее в командную область с помощью оператора disp.
Шаг 4. Для вычисления произведения проделываем ту же самую последовательность шагов, только воспользуемся стандартной функцией prod.
| Программа | Результаты расчетов | Программа | Результаты расчетов |
| i=1:8F=(i+3).*(i-6)SS=sum(F)disp(SS) | — 48. | i=1:5F1=(i+2*i-1)PP=prod(F1) disp(PP) | 12320. |
Индивидуальные варианты приведены в таблице 2.5.
Таблица 2.5
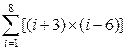 | 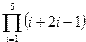 | ||
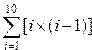 | 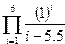 | ||
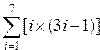 | 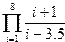 | ||
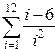 | 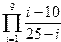 | ||
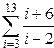 | 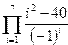 | ||
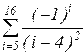 | 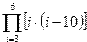 | ||
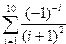 | 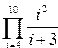 | ||
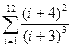 | 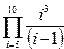 | ||
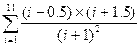 | 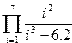 | ||
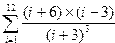 | 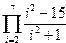 | ||
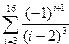 | 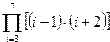 | ||
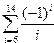 | 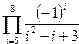 | ||
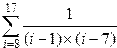 | 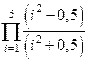 | ||
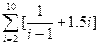 | 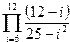 | ||
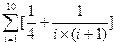 | 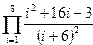 |
Задание 5. Решение задач с матрицами
Постановка задачи.Дана матрица Y(3´4). Вычислить сумму элементов третьей строки и произведение элементов второго столбца матрицы Y. Вычислить максимальный элемент матрицы Y.
Порядок составления программы таков.
Шаг 1. Создаем матрицу, элементы которой подберем самостоятельно. Выведем матрицу в командную область.
Шаг 2. С помощью стандартной функции sum найдем сумму элементов третьей строки, для этого укажем Y(3,:), что означает – третья строка и все столбцы в ней. Поместим сумму в переменную S и выведем результат в командную область.
Шаг 3. Для вычисления произведения проделываем ту же самую последовательность шагов, только воспользуемся стандартной функцией prod и выбираем второй столбец матрицы — Y(:,2). Поместим произведение в переменную S1 и выведем ее в командную область.
Шаг 4. Для вычисления максимума воспользуемся стандартной функцией max, и так как нужно вычислить максимум среди всех элементов матрицы, то номер строки и столбца не указываем. Поместим результат в переменную М и выведем его в командную область.
| Программа | Результаты расчетов |
| Y=[2 -1 -3 8; -7 -6 -3 4; 2 5 8 2]disp(Y)S=sum(Y(3,:))disp(S)S1=prod(Y(:,2))disp(S1)M=max(Y)disp(M) | 2. — 1. — 3. 8.- 7. — 6. — 3. 4.2. 5. 8. 2.17.30.8. |
Индивидуальные варианты приведены в таблице 2.6.
Таблица 2.6
| № | Дана матрица | Вычислить |
| Y(3´4) | Вычислить сумму элементов третьей строки и произведение элементов второго столбца матрицы Y.Вычислить максимальный элемент матрицы Y. | |
| P(4´3) | Вычислить сумму элементов второй строки и произведение элементов третьего столбца матрицы P.Вычислить максимальный элемент матрицы P. | |
| M(4´4) | Вычислить сумму элементов последней строки и произведение элементов первого столбца матрицы M.Вычислить минимальный элемент матрицы M.. | |
| A(3´3) | Вычислить сумму элементов второй строки и произведение элементов третьего столбца матрицы А.Вычислить минимальный элемент матрицы A. | |
| Y(3´4) | Вычислить сумму элементов второй строки и второго столбца матрицыВычислить минимальный элемент матрицы Y. | |
| P(4´3) | Вычислить произведение элементов третьей строки и третьего столбца матрицы P.Вычислить максимальный элемент матрицы P. | |
| M(4´4) | Вычислить сумму элементов последней строки и первого столбца матрицы M.Вычислить максимальный элемент матрицы М. | |
| A(3´3) | Вычислить произведение элементов второй строки и третьего столбца матрицы А.Вычислить максимальный элемент матрицы А. | |
| Z(4´3) | Вычислить среднее арифметическое элементов второго столбца матрицы Z.Вычислить минимальный элемент матрицы Z. | |
| P(4´5) | Вычислить среднее арифметическое элементов второй строки матрицы P.Вычислить минимальный элемент матрицы Р. | |
| M(4´4) | Вычислить сумму элементов последней строки и произведение элементов первого столбца матрицы M.Вычислить сумму элементов матрицы М | |
| A(3´3) | Вычислить сумму элементов второй строки и минимальный элемент третьего столбца матрицы А.Вычислить произведение элементов матрицы A. | |
| Y(3´4) | Вычислить максимальный элемент второй строки и произведение элементов второго столбца матрицы Y.Вычислить сумму элементов матрицы Y. | |
| P(4´3) | Вычислить сумму элементов третьей строки и максимальный элемент третьего столбца матрицы P.Вычислить произведение элементов матрицы Р. | |
| M(4´4) | Вычислить сумму элементов последней строки и минимальный элемент первого столбца матрицы M.Вычислить произведение элементов матрицы М. |
Программирование в Scilab
Краткие теоретические сведения
Для программирования разветвляющихся алгоритмов в Scilab существуют оператор условия и оператор выбора.
Условный оператор представлен в нескольких формах и имеет следующий общий вид.
Полная форма 1
If ЛВ then
ОПЕРАТОР1
Else ОПЕРАТОР2,
End
Полная форма 2
If ЛВ
Then ОПЕРАТОР1,
Статьи к прочтению:
How to plot 2D graphs in Scilab [TUTORIAL]
Похожие статьи:
-
Данные, их типы, структуры и обработка
Любая актуализация информации опирается на какие-то данные, любые данные могут быть каким-то образом актуализированы. Данные – это некоторые сообщения,…
-
1. Ввести файл из 14 элементов. Определить в нём произведение элементов, квадрат которых меньше 16. 2. Ввести файл из 13 элементов. Определить в нём…
