Основные теоретические сведения. рассмотрим следующую задачу.
Рассмотрим следующую задачу.
Даны натуральные числа  . Найти среди них максимальное.
. Найти среди них максимальное.
Одно из решений данной задачи представлено в листинге 19.
| Листинг 19 |
/*Поиск максимума среди 5-ти чисел*/
#include
#include
#include
void main( void )
{
// Объявление переменных для чисел а1,…,а5
int nArray1, nArray2, nArray3, nArray4, nArray5;
cout
cinnArray1; // Ввод числа а1
cout
cinnArray2; // Ввод числа а2
cout
cinnArray3; // Ввод числа а3
cout
cinnArray4; // Ввод числа а4
cout
cinnArray5; // Ввод числа а5
int nResult = nArray1; // Объявление и инициализация переменной
// для хранения результата
if ( nResultnArray2 ) nResult = nArray2;
if ( nResultnArray3 ) nResult = nArray3;
if ( nResultnArray4 ) nResult = nArray4;
if ( nResultnArray5 ) nResult = nArray5;
cout
}
После изучения листинга 19 и многих возникнет вопрос, что делать, если чисел а по условию задачи будет не 5, а 100, 200 или даже 1000? Очевидно, что приведенное решение не самое ффективное.
Одномерные массивы
В лабораторной работе №2 мы отмечали, что переменные можно рассматривать как некие именованные ящики, а значения переменных – как содержимое этих ящиков. Чтобы получить доступ к содержимому ящика надо знать его имя. Также мы уже знаем, что все переменные в языке Си++ перед использованием надо объявлять. Например, запись:
int nNumber;
означает, что мы подготовили к использованию очередной ящик, дали ему имя «nNumber» и в дальнейшем будем в этом ящике хранить одно целое число. Число может быть любым, и в любой момент времени мы можем поменять его значение.
Теперь рассмотрим полку, на которой стоят однотипные ящики. Присвоим полке имя «Array». Язык Си++ позволяет объединить все ящики, находящиеся на этой полке в одну группу под общим именем самой полки. Такие группы называются массивами.
Предположим, на нашей полке Array находится 5 ящиков и в каждом хранится целое число. Тогда каждый ящик-ячейка имеет имя:
Array[0]
Array[1]
Array[2]
Array[3]
Array[4]
Обратите внимание, что нумерация ящиков идет с НУЛЯ.
Как и переменные, массивы следует объявлять перед использованием. В нашем случае:
int Array[5];
Это описание как бы объявляет пять переменных типа int с именами Array[0] … Array[4].
В программе для обращения к i-му ящику используется его имя Array[i], где i – целое значение называемое «индексом в массиве». Операция [] называется «индексация массива». Индексация – есть выбор одного из N (в нашем случае N = 5) ящиков при помощи указания целого номера.
Как и переменные, массивы надо инициализировать (присваивать элементам массива начальные значения) после объявления.
Массивы нельзя присваивать целиком. Язык Си++ этого не умеет. Запись
int nArray1[3];
int nArray2[3];
nArray1 = nArray2;
является ошибкой. Также нельзя присвоить значение сразу всем элементам массива и в данном контексте запись:
int nArray1 = 0;
является ошибочной.
Для обнуления всех элементов нашего массива Array следует воспользоваться циклом:
for ( int i = 0; i5; i++ )
{
Array[i] = 0;
}
В нашем случае массив Array есть пример статического одномерного массива.
Термин «статический» означает, что размер массива заранее известен и в дальнейшем не меняется.
Рассмотрим теперь пример использования одномерного массива для решения задачи поиска максимального из пяти чисел одно из решений которой было дано в листинге 19.
| Листинг 20 |
/*Поиск максимума из 5-ти чисел
с использованием одномерного массива*/
#include
#include
#include
void main( void )
{
// Объявление массива для чисел а1,…,а5
int nArray[5];
for ( int i = 0; i5; i++ )
{
cout
cinnArray[i]; // Ввод числа аi
}
int nResult = nArray[0]; // Объявление и инициализация переменной
// для хранения результата
// Поиск максимального числа
for ( i = 1; i5; i++ )
{
if ( nResultnArray[i] ) nResult = nArray[i];
}
cout
}
Одномерные массивы очень удобны при работе со строками. Строки есть массивы символов типа char оканчивающиеся специальным символом ‘\0’.
char szString[20];
szString[0] = ‘H’;
szString[1] = ‘e’;
szString[2] = ‘l’;
szString[3] = ‘l’;
szString[4] = ‘0’;
szString[5] = ‘\0’;
printf( “%s\n”, szString );
Вывод:
Hello
Приведенный пример демонстрирует одно очень удобное свойство массивов типа char, их можно передавать в качестве аргумента функции printf(), что позволяет легко распечатывать содержимое таких массивов.
char szString[20];
szString[0] = ‘H’;
szString[1] = ‘e’;
szString[2] = ‘l’;
szString[3] = ‘l’;
szString[4] = ‘0’;
szString[5] = ‘\n’;
szString[6] = ‘w’;
szString[7] = ‘o’;
szString[8] = ‘r’;
szString[9] = ‘l’;
szString[10] = ‘d’;
szString[11] = ‘\n’;
szString[12] = ‘\0’;
printf( “%s”, szString );
Вывод:
Hello
world
Такие массивы можно инициализировать совместно с объявлением:
char szString[20] = “Hello\n”;
Оставшиеся неиспользованными элементы массива от szString[6] до szString[19] содержат мусор т.е. любое заранее неизвестное значение.
Также одномерные массивы можно использовать при работе с рядами. Например, в листинге 21 приведен код программы печатающей первые 20 чисел Фибоначчи которые определяются по следующему правилу:
F1 = 1;
F2 = 1;
Fi = Fi-1 + Fi-2 , при i2;
| Листинг 21 |
/*Магические числа Фибоначчи*/
#include
void main( void )
{
int nFib[20], nIndex;
nFib[0] = 1;
nFib[1] = 1;
// Тут показано, что индекс элемента массива может вычисляться
for ( nIndex = 2; nIndex20; nIndex++ )
{
nFib[nIndex] = nFib[nIndex — 1] + nFib[nIndex — 2];
}
// Распечатка в обратном порядке
for ( nIndex = 19; nIndex = 0; nIndex— )
{
printf(“%d-th Fibonachi number is%d\n”, nIndex, nFib[nIndex] );
}
}
Двумерные массивы
Представим теперь вместо полки с ящиками, библиотечный каталог, т.е. шкаф с множеством ящиков организованных по принципу рядов и колонок. Каждый такой шкаф также является массивом, но уже двумерным.
Вот пример объявления двумерного массива:
int nArray[2][3];
int nArray[0][0] – 1-й элемент 1-й строки;
int nArray[0][1] – 2-й элемент 1-й строки;
int nArray[0][2] – последний элемент 1-й строки;
int nArray[1][0] – 1-й элемент 2-й строки;
int nArray[1][1] – 2-й элемент 2-й строки;
int nArray[1][2] – последний элемент 2й, последней, строки;
Двумерный массив nArray рассматривается как массив массивов. Элементами главного массива nArray являются два одномерных массива nArray[0] и nArray[1], каждый из которых состоит из трех элементов типа int.
В листинге 22 приведен пример программы, печатающей на экране содержимое массива nArray.
| Листинг 22 |
/*Печать содержимого двумерного массива*/
#include
void main( void )
{
// Пример начальной инициализации массива при его объявлении
int nArray[2][3] = {{1,2,3},
{4,5,6}};
// Печать содержимого массива
printf( Massiv nArray[2][3]
\nnArray[0][0] = %d
\nnArray[0][1] = %d
\nnArray[0][2] = %d
\nnArray[1][0] = %d
\nnArray[1][1] = %d
\nnArray[1][2] = %d\n,
nArray[0][0], nArray[0][1], nArray[0][2],
nArray[1][0], nArray[1][1], nArray[1][2] );
}
Алгоритмы
Внимание! Начиная с данной лабораторной работы, студенты должны приводить в протоколах алгоритмы решенных задач.
Существует множество определений термина «алгоритм». Некоторые более понятны некоторые – менее. Мы начнем с простых жизненных примеров.
Когда вы собираетесь приготовить суп, то делаете это по определенному рецепту, например, помыть мясо, нарезать его, положить в кастрюлю, залить водой и т.д. Этот рецепт является алгоритмом. Когда вы занимаетесь побелкой комнаты, вы также делаете это по определенной технологии. Например, предварительно закрыть мебель газетами или тряпками, размешать краску, побелку осуществлять сверху вниз и т.п. Такая технология также является алгоритмом.
В общем случае давайте называть алгоритмом любую упорядоченную по любому признаку последовательность действий необходимых для достижения результата. Например, Утром встали, позавтракали, пошли в университет и т.д.
В данном лабораторном практикуме вы уже сталкивались с алгоритмами в лабораторной работе №1 когда изучали последовательности действий при установке пакетов Turbo C и Visual C++ 6.0. Последовательности действий необходимые для создания проекта, написания программного кода, компиляции и запуска программы и т.д. также являются алгоритмами.
В рамках лабораторной работы №2 вы сталкивались с алгоритмами в ходе решения каждой из трех задач. Перед написанием программного кода вы волей-неволей планировали последовательность своих действий. Сначала объявить переменные. Затем ввести исходные данные. Если при компиляции возникла ошибка, то проверить правильность подключения библиотеки и т.д. Такое планирование опять таки можно рассматривать как алгоритм.
Несмотря на то, что студенты упорно пытаются сначала написать программу, а затем оформить по ней алгоритм это неверно. Такой подход срабатывает при написании простых программ с тривиальными алгоритмами. На практике, программное обеспечение может представлять собой сложный комплекс различных модулей, функций, классов и т.д. Если заранее не спланировать алгоритм взаимодействия всех элементов ПО, не проанализировать логику этих взаимодействий, то в итоге можно получить ПО не способное выполнять свои функции. Возможен также вариант когда вам придется переделывать все ПО с самого начала.
Поэтому студентам настоятельно рекомендуется разрабатывать алгоритмы перед написанием программного кода.
Для записи алгоритмов мы будем пользоваться двумя формами: словесной и в виде блок-схем (правила оформления блок-схем вы можете найти в ГОСТ 19.701).
Рассмотрим алгоритм решения следующей задачи.
Дана действительная квадратная матрица порядка n. Определить количество положительных элементов матрицы расположенных на главной диагонали.
Алгоритм решения этой задачи приведен на рис. 14
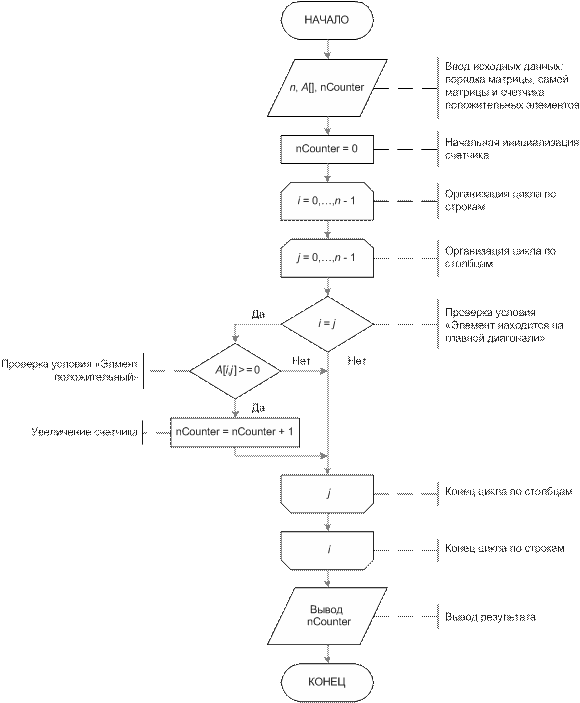
Рис. 14.
Представленная форма записи называется блок-схемой или схемой алгоритма.
Ниже представлен этот же алгоритм в виде словесного описания.
АЛГОРИТМ 1
Исходные данные:
n — порядок матрицы;
А[n?n] — действительная матрица.
Выходные данные:
nCounter — количество положительных элементов матрицы расположенных на главной диагонали.
Вспомогательные переменные:
i, j — переменные для организации циклов.
Шаг 1. [Установить nCounter]. nCounter = 0. (Обнулить счетчик элементов).
Шаг 2. [Цикл по i]. Выполнить шаг 3 при i = 0,…,n – 1 и после этого завершить алгоритм.
Шаг 3. [Цикл по j]. Выполнить шаги от 4 до 6 при j = 0,…,n – 1.
Шаг 4. [Сравнить i, j]. Если i = j то перейти к шагу 5, иначе к шагу 3. (Проверяем, находится ли элемент на главной диагонали).
Шаг 5. [Сравнить А[i,j], 0]. Если А[i,j] = 0 то перейти к шагу 6, иначе к шагу 3. (Проверяем, является ли элемент положительным).
Шаг 6. [Установить nCounter]. nCounter = nCounter + 1. (Увеличиваем счетчик положительных элементов).
В приведенном словесном алгоритме в квадратных скобках указаны типы действий, в круглых — комментарии к действиям, а между ними — суть этих действий.
Как видно, каждая из форм записи обладает своими достоинствами и недостатками. В дальнейшем мы будем пользоваться обеими формами.
Обратите внимание, что алгоритмы не включают в себя последовательность действий по вводу/выводу информации. Подобные операции, которые можно назвать стандартными или типовыми, нет надобности описывать в алгоритмах. Каждый алгоритм должен объяснять суть решения поставленной задачи. Не как осуществить ввод/вывод информации и т.п., а как преобразовать эту информацию чтобы добиться желаемого результата.
Решение типовых задач
Задача 1. Даны целые числа а1,…,а10 и целочисленная квадратная матрица порядка n. Заменить нулями в матрице те элементы с четной суммой индексов, для которых имеются равные среди а1,…,а10.
Решение.
В общем, виде данная задача на ЭВМ не имеет решения (ЭВМ не в состоянии оперировать со всем диапазоном натуральных чисел), поэтому примем дополнительные ограничения.
Пусть диапазон изменения чисел а1,…,а10 и элементов матрицы принадлежит интервалу [0, 50]. Примем порядок матрицы 1n
Алгоритм решения в виде блок-схемы представлен на рис. 15.
Ниже дан алгоритм решения в виде словесного описания.
АЛГОРИТМ 2
Алгоритм позволяет заменить нулями каждый элемент матрицы с четной суммой индексов если он равен одному из элементов вектора А.
Исходные данные:
n — порядок матрицы;
А[10] — вектор натуральных чисел.
M[n?n] — действительная матрица.
Выходные данные:
M[n?n] — преобразованная исходная матрица.
Вспомогательные переменные:
i, j, k — переменные для организации циклов.
Шаг 1. [Установить nCounter]. nCounter = 0. (Обнулить счетчик элементов).
Шаг 2. [Цикл по i]. Выполнить шаг 3 при i = 0,…,n – 1 и после этого завершить алгоритм.
Шаг 3. [Цикл по j]. Выполнить шаг 4 при j = 0,…,n – 1.
Шаг 4. [Сравнить i, j]. Если остаток от деления суммы (i + j) на 2 отличен от нуля, то перейти к шагу 3, иначе к шагу 5. (Проверяем, является ли сумма индексов элемента матрицы четной).
Шаг 5. [Цикл по k]. Выполнить шаг 6 при k = 0,…,9. (Осуществляем перебор всех элементов вектора А).
Шаг 6. [Сравнить М[i,j], А[k]]. Если М[i,j] = A[k], то присвоить М[i,j] = 0. перейти к шагу 3, иначе к шагу 5. (Проверяем, есть ли среди элементов вектора А равные текущему элементу матрицы М. Если да, то заменяем элемент матрицы на нуль).
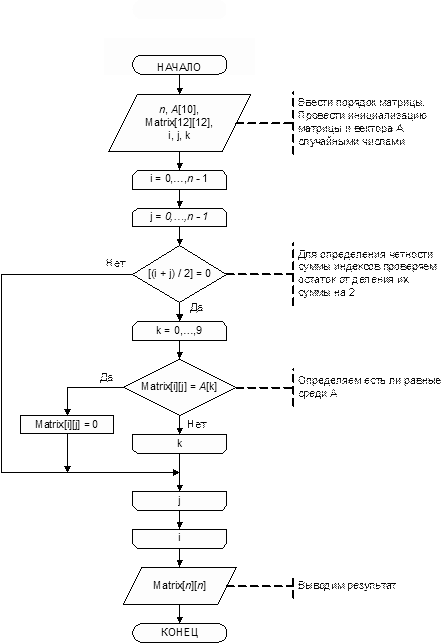
Рис. 15.
Программный код представлен в листинге 23.
| Листинг 23 |
/*Лабораторная работа №3*/
#include
#include
#include
void main( void )
{
// Инициализация генератора случайных чисел
srand((unsigned)time(NULL));
// Вспомогательные переменные для организации циклов
int i, j, k;
int nSourceArray[12][12];
int nA[10];
// Порядок матрицы
int nOrder;
// Запрос ввода порядка матрицы и выход в случае
// ввода неверного порядка
cout
cinnOrder;
if (( nOrder12 ))
{
cout
return;
}
// Инициализация исходной матрицы и ее вывод на экран
cout
// Используется только необходимая для работы часть массива
for ( i = 0; inOrder; i++ )
{
for ( j = 0; jnOrder; j++ )
{
// Инициализируем случайными числами от 0 до 50
nSourceArray[i][j] = 50 * rand() / RAND_MAX;
cout
}
cout
}
// Генерируем значения вектора А
cout
for ( i = 0; i10; i++ )
{
nA[i] = 50 * rand() / RAND_MAX;
cout
}
cout
// Преобразуем исходную матрицу
for ( i = 0; inOrder; i++ )
{
for ( j = 0; jnOrder; j++ )
{
// Проверка четности суммы индексов
if ((( i + j ) % 2 ) == 0 )
{
for ( k = 0; k10; k++ )
{
// Проверка есть ли в векторе А элементы равные
// текущему элементу матрицы
if ( nSourceArray[i][j] == nA[k] )
{
nSourceArray[i][j] = 0;
// Прерываем цикл по k и выходим из него
break;
}
}
}
}
}
// Выводим на экран преобразованную матрицу
cout
for ( i = 0; inOrder; i++ )
{
for ( j = 0; jnOrder; j++ )
{
cout
}
cout
}
}
Варианты заданий
| № | Задание |
Даны целые числа 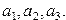 Получить целочисленную матрицу Получить целочисленную матрицу 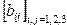 , для которой , для которой 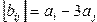 | |
Даны действительные числа 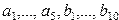 Получить действительную матрицу Получить действительную матрицу 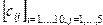 , для которой , для которой 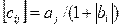 | |
Получить целочисленную матрицу 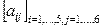 , для которой , для которой 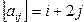 | |
Получить целочисленную матрицу 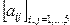 , для которой первая строка задается формулой , для которой первая строка задается формулой 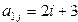 , вторая строка задается формулой , вторая строка задается формулой 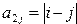 , а каждая следующая строка есть сумма двух предыдущих , а каждая следующая строка есть сумма двух предыдущих | |
| Даны натуральное число n, действительная матрица n?6. Найти среднее арифметическое каждого из столбцов | |
| Даны натуральное число n, действительная матрица 6?n. Найти среднее арифметическое каждого из столбцов имеющих четные номера | |
Дано натуральное число n. Выяснить сколько положительных элементов содержит квадратная матрица порядка n если 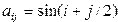 | |
| Дана действительная матрица размера n?m. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент. | |
| Дана действительная квадратная матрица порядка 5. Заменить нулями все элементы расположенные на главной диагонали и выше нее. | |
Даны натуральные числа  . Получить квадратную матрицу порядка 4 . Получить квадратную матрицу порядка 4 | |
Дана действительная матрица размера m?n. Определить числа  равные значениям средних арифметических элементов строк. равные значениям средних арифметических элементов строк. | |
Даны натуральное число n и действительная матрица 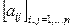 . Получить последовательность элементов главной диагонали . Получить последовательность элементов главной диагонали  | |
| Дана действительная матрица размера m?n. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов. | |
| Дана действительная матрица размера 8?n. Найти значение наибольшего по модулю элемента матрицы, а также индексы какого-нибудь элемента с найденным значением модуля. | |
| Дана действительная матрица размера m?n. Найти сумму наибольших значений элементов строк. | |
Дана действительная матрица размера m?n. Получить последовательность  , где , где 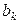 – наибольшее из значений k-ой строки. – наибольшее из значений k-ой строки. | |
| Дана целочисленная квадратная матрица порядка 6. Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них. | |
| Дана действительная квадратная матрица порядка 8. В строках с отрицательным элементом на главной диагонали найти сумму всех элементов. | |
| Дана действительная квадратная матрица порядка 8. Получить целочисленную квадратную матрицу того же порядка, в которой элемент равен 1, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, и равен нулю в противном случае. | |
| Дана действительная квадратная матрица порядка n и числа i,j (1 ? i ? n, 1 ? j ? n). Удалить из матрицы i–ю строку и j–й столбец. |
Контрольные вопросы
1) Как получить доступ к элементам массива?
2) Вы используете в программе двумерный массив размером 1000?1000. Вам необходимо провести начальную инициализацию элементов этого массива. Инициализация заключается в присвоении каждому элементу массива случайного значения. Ваши действия?
3) Вы знаете, что статические массивы имеют заранее определенный размер. По условию задачи вам необходимо в качестве исходных данных использовать матрицы произвольного размера в пределах от 2 до 20. Ваши действия?
4) Приведите алгоритм решения любой из задач данной лабораторной работы кроме своего варианта.
Лабораторная работа №4
Цель: усовершенствовать навыки программирования на примере решения задач матричной алгебры.
Задачи:
1) Повторить теоретические сведения о создании и использовании статических массивов в языке Си++.
2) Разработать программу решающую одну из задач матричной алгебры.
Статьи к прочтению:
- Основные теоретические сведения. в лабораторных работах 3 и 4 мы решали задачи со статическими массивами
- Основные теоретические сведения. внимание! выполнение данной лабораторной работы предполагает, что студенты в полном объеме изучили материал
А.И. Соколов про квантовую механику, часть первая
Похожие статьи:
-
Внимание! Выполнение данной лабораторной работы предполагает, что студенты в полном объеме изучили материал, изложенный в лабораторной работе №1. Если у…
-
В лабораторных работах 3 и 4 мы решали задачи со статическими массивами. Размер статического массива определяется еще на этапе компиляции. Работа с…
