Перевод чисел из одной системы счисления в другую.

Лекция №4 Системы счисления.

План

1. Непозиционные и позиционные системы счисления.

2. Системы счисления, используемые в электронно-вычислительных машинах.

3. Перевод чисел из одной системы счисления в другую.

Непозиционные и позиционные системы счисления.

Система счисления – это совокупность приемов и правил, по которым числа записываются и читаются.

Системы счисления делятся на:

1. В непозиционных система счислениявес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

2. В позиционных системах счислениявес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – единиц, а третья – 7 десятых долей единиц.

Сама же запись числа 757,7 означает сокращенную запись выражения:

700 + 50 + 7 + 0,7 = .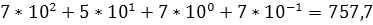

Любая позиционная система счисления характеризуется свои основанием.

Основание позиционной системы счисления – количество различных цифр, используемых для изображения чисел в данной системе счисления.

За основание системы можно принять любое натуральное число – два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем:двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения:

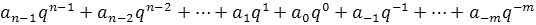где 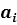– цифры системы счисления, n и m – число целых и дробных разрядов, соответственно.

Например:

Разряды 3 2 1 0 -1

Число 1 0 1 1, = ,

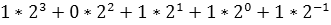Разряды 2 1 0 -1 -2

Число 2 7 6, 5 = ,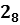

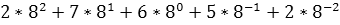Системы счисления, используемые в электронно-вычислительных машинах.

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

двоичная(используются цифры 0,1);
восьмеричная (используются цифры 0,1,…, 7);
шестнадцатеричная(для первых целых чисел от нуля до девяти используются цифры 0,1, …, 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы А, B, C, D, E, F).

Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная










			A
			B
			C
			D
			E
			F

Из всех систем счисления особенно простаи поэтому интересна для технической реализации в компьютерах двоичная система счисления.

Перевод чисел из одной системы счисления в другую.

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:

Таблица 4. Степени числа 2

n (степень)

Пример .Число перевести в десятичную систему счисления.

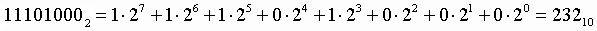
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:

Таблица 5. Степени числа 8

n (степень)

Пример.Число 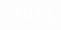перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:

Таблица 6. Степени числа 16

n (степень)

Пример .Число перевести в десятичную систему счисления.

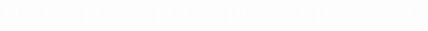
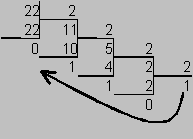
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример.Число перевести в двоичную систему счисления.

Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример.Число перевести в восьмеричную систему счисления.

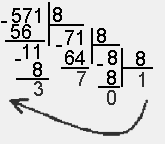
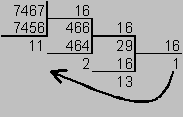
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример.Число перевести в шестнадцатеричную систему счисления.

Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример.Число 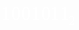перевести в восьмеричную систему счисления.

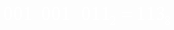
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример.Число 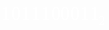перевести в шестнадцатеричную систему счисления.

Статьи к прочтению:

Перевод чисел.avi

Похожие статьи: