Прямое произведение множеств.
Пусть даны какие-нибудь объекты а и b. Множество 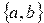 называется неупорядоченной парой объектов а и b, если для данных объектов не задан порядок их следования. В противном случае, имеем дело с упорядоченной парой
называется неупорядоченной парой объектов а и b, если для данных объектов не задан порядок их следования. В противном случае, имеем дело с упорядоченной парой 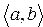 , где а называют первым элементом пары, а b – вторым элементом пары. Также отметим, что
, где а называют первым элементом пары, а b – вторым элементом пары. Также отметим, что 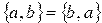 . Определим равенство для упорядоченных пар.
. Определим равенство для упорядоченных пар.
Определение 1. Упорядоченные пары 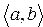 и
и 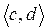 называют равными и пишут
называют равными и пишут 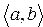 =
= 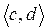 в том и только в том случае, когда
в том и только в том случае, когда  ,
, 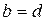 .
.
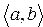 =
= 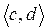
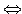

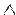
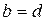
В частности, 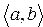 =
= 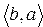
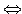

Определение 2. Прямым произведением множеств А и В называется множество всех упорядоченных пар 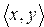 таких, что
таких, что  и
и 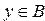 . Это множество обозначается
. Это множество обозначается 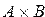 .
.
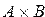 =
= 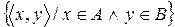
Пример.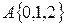
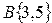
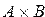 =
= 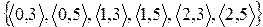
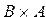 =
= 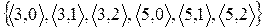
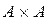 =
= 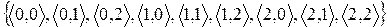
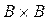 =
= 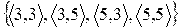
Обобщением понятия упорядоченной пары является понятие кортежа(упорядоченного набора n). Кортеж n объектов а1, а2, …,аn обозначается через 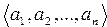 .
.
Определение 3. Два кортежа 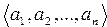 и
и 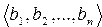 называют равными и пишут
называют равными и пишут 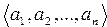 =
= 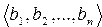 в том и только в том случае, когда
в том и только в том случае, когда 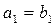 ,
,  , …,
, …, 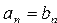 .
.
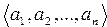 и
и 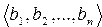
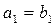

 …
… 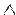
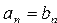
Определение 4. Прямым произведением n-множеств А1, А2, …, Аn называется множество всех кортежей длины n 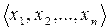 таких, что
таких, что 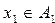 ,
, 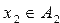 , …,
, …, 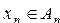 .
.
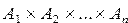 =
= 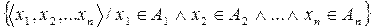
Бинарные отношения.
Бинарным отношениемназывается любое множество упорядоченных пар.
Из этого определения следует, что бинарным отношением является любое подмножество прямого произведения множеств.
Если R – бинарное отношение и 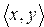
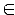 R, то говорят , что х и у связаны отношением R, или что элемент х находится в отношении R к элементу у, или что для х, у выполняется отношение R. Вместо записи
R, то говорят , что х и у связаны отношением R, или что элемент х находится в отношении R к элементу у, или что для х, у выполняется отношение R. Вместо записи 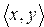
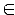 R используют хRу.
R используют хRу.
Способы задания бинарных отношений – любые способы задания множеств. Отношения, определенные на конечных множествах обычно задаются:
списком (перечислением) пар, для которых это отношение выполняется, например 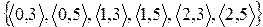 .
.
квадратной матрицей, в которой элемент сij равен 1, если бинарное отношение выполняется, и равно 0 в противном случае.
Определение 5. Множество всех первых элементов пар из R называется областью определения отношения R и обозначается Dom R.
Dom R = 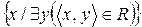
Определение 6. Множество всех вторых элементов пар из R называется областью значений отношения R и обозначается Im R.
Im R = 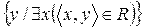
Определение 7. Множество Dom R 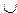 Im R называется областью отношения R.
Im R называется областью отношения R.
R  Dom R
Dom R  Im R
Im R
Замечания.
Если R 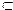 А
А  В, то говорят, что R определено на паре множеств А и В.
В, то говорят, что R определено на паре множеств А и В.
Если R 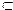 А
А  В и А
В и А  С, В
С, В  D, то R
D, то R 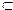 С
С  D.
D.
Если R 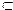 А
А  В, то Dom R
В, то Dom R  А, Im R
А, Im R 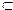 В.
В.
Если R 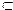 А
А  А, то говорят, что есть R бинарное отношение на множестве А.
А, то говорят, что есть R бинарное отношение на множестве А.
Определение 9. Пусть R и S — бинарные отношения. Множество всех пар 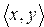 таких, что для некоторого z , связанного отношениями R и S
таких, что для некоторого z , связанного отношениями R и S 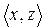
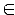 R и
R и 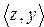
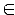 S, называется композицией (или суперпозицией) отношений R и S и обозначается через R*S.
S, называется композицией (или суперпозицией) отношений R и S и обозначается через R*S.
R*S= 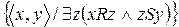
Пример. R= 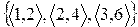 и S=
и S= 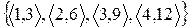
 R*S=
R*S= 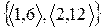 .
.
Вопросы для активизации и создания проблемной ситуации.
1. Дайте понятие множества и его элементов. Приведите примеры. Каким образом обозначаются множества и его элементы, как указывается принадлежность элемента к множеству?
2. Какие множества называются равными? Приведите примеры равных множеств.
3. Дайте определение подмножества множества. Приведите примеры.
4. Перечислите свойства отношения включения.
5. Дайте определение пустому множеству. Как обозначается пустое множество?
6. Как подсчитать количество подмножеств множества. Приведите пример.
7. Дайте определение объединению множеств. Приведите пример.
8. Дайте определение пересечению множеств. Приведите пример.
9. Дайте определение разности множеств. Приведите пример.
10. Перечислите основные свойства операций над множествами.
11. Какое множество называется универсальным? Примеры.
12. Что называется дополнением множества?
13. Как графически изображаются множества и их свойства?
14. Какие пары объектов называются неупорядоченными, какие упорядоченными?
15. Определите равенство для случаев неупорядоченной пары и упорядоченной пары.
16. Дайте определение прямого произведения множеств.
17. Что называют бинарным отношением?
18. Как связаны бинарные отношения с прямым произведением множеств?
19. Что называют областью определения бинарного отношения?
20. Что называют областью значений бинарного отношения?
21. Что называют областью бинарного отношения?
22. Как находить композицию двух бинарных отношений?
Лекция №3. Основы логики, логика высказываний, логические связки, таблицы истинности (1 час)
Цель лекции: Рассмотреть основные положения алгебры логики: объекты языка, определение алгебры логики, функции в алгебре логики и способы их задания. Дать понятие высказывания; рассмотреть основные операции над высказываниями.
Вопросы лекции:
1. Основы алгебры логики.
2. Понятие высказывания.
3. Логические операции над высказываниями, логические связки, таблицы истинности.
4. Формулы логики высказываний.
5. Законы логики.
6. Логическое следствие.
Содержание лекции:
Основы алгебры логики.
Рассмотрим содержание логики высказываний, используя язык алгебры логики. В алгебре логики логические формулы рассматриваются как алгебраические выражения, которые можно преобразовывать по определенным правилам, реализующим логические законы.
Основные объекты алгебры логики – формулы, состоящие из букв, знаков логических операций и скобок. Буквы обозначают логические переменные, которые могут принимают значения «истина» или «ложь». Каждая формула задает логическую функцию – функцию от логических переменных и может также принимать два логических значения.
Пусть В={0, 1} – бинарное множество, элементами которого являются формальные символы 1 и 0, не имеющие арифметического смысла и интерпретируемые как «истинно», «ложно».
Алгебра логики — алгебра, образованная множеством В={0, 1} вместе со всеми возможными операциями на нем.
Любую логическую функцию f(x1,x2,…..,xn) как и в логике высказываний можно задать таблицей истинности. Набор значений переменных, на котором функция принимает значение f =1, называется единичным набором функции f; множество всех единичных наборов – единичным множеством функции f. Аналогично, набор значений, на котором f =0, называется нулевым набором функции f, а множество нулевых наборов – нулевым множеством.
Число всех возможных различающихся наборов значений n переменных логической функции f(x1,x2,…..,xn) равно 2n.
Понятие высказывания.
Понятие «высказывание» первично. Под высказыванием в логике понимают повествовательное предложение, о котором можно говорить истинно оно или ложно. Например, предложение «Город Экибастуз находится в Павлодарской области» является истинным высказыванием; а предложение «В сутках 25 часов» является ложным высказыванием. Любое высказывание либо истинно, либо ложно, и никакое высказывание не является одновременно и истинным и ложным. В логике высказываний отвлекаются от смыслового содержания высказывания, ограничиваясь лишь рассмотрением его с той позиции, что оно истинно, либо ложно. Однако следует помнить, что вопросительные и восклицательные предложения, а также определения высказываниями являться не будут. Например, предложения « С Новым годом!», «Когда будет полнолуние?», «Красивая девушка» не являются высказываниями.
Статьи к прочтению:
Интуитивная топология | теоретико множественные вопросы | декартово произведение
Похожие статьи:
-
Альтернативой явному перечислению элементов множества является set-нотация, где мы помещаем имя обобщенного элемента множества и через двоеточие…
-
Для описания асимптотических оценок имеется система нотаций: § Говорят, что f(n)=O(g(n)), если существует такая константа c0 и такое число n0, что…
