Программирование машины тьюринга

      Комментарии к записи Программирование машины тьюринга отключены

Машина Тьюринга — это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван “машиной” по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту: у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.

В каждой машине Тьюринга есть две части:

1) неограниченная в обе стороны лента, разделенная на ячейки;

2) автомат (головка для считывания/записи, управляемая программой).

С каждой машиной Тьюринга связаны два конечных алфавита: алфавит входных символов A = {a0, a1, …, am}и алфавит состояний Q = {q0, q1, …, qp}. (С разными машинами Тьюринга могут быть связаны разные алфавиты A и Q.) Состояние q0называется пассивным. Считается, что если машина попала в это состояние, то она закончила свою работу. Состояние q1 называется начальным. Находясь в этом состоянии, машина начинает свою работу.

Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит пустая буква а0 — признак того, что ячейка пуста).

Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.

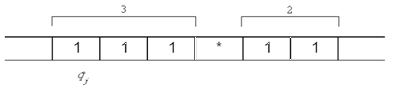
Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую буквуai он видит, а также в зависимости от своего состояния qj автомат может выполнять следующие действия:

  • · записать новую букву в обозреваемую ячейку;
  • · выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
  • · перейти в новое состояние.

То есть у машины Тьюринга есть три вида операций. Каждый раз для очередной пары (qj, ai) машина Тьюринга выполняет команду, состоящую из трех операций с определенными параметрами.

Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.

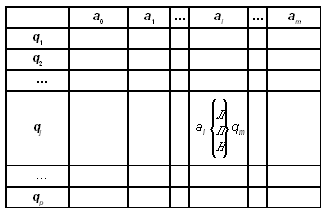
Клетка (qj, ai) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: куда передвинуть головку чтения/записи, какой символ записать в текущую ячейку, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).

После выполнения автоматом очередной команды он переходит в состояние qm(которое может в частном случае совпадать с прежним состоянием qj). Следующую команду нужно искать в m-й строке таблицы на пересечении со столбцом al (букву alавтомат видит после сдвига).

Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в состоянии q1. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q0. Эти клетки называются клетками останова. Дойдя до любой такой клетки, машина Тьюринга останавливается.

Несмотря на свое простое устройство, машина Тьюринга может выполнять все возможные преобразования слов, реализуя тем самым все возможные алгоритмы.

Машина Поста

Машина Поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом, которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».

Принцип работы

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты (см. пример ниже). Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит. Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из строк команд. Каждая команда имеет следующий синтаксис:

I K j,

где i — номер команды, K – действие каретки, j — номер следующей команды (отсылка).

Всего для машины Поста существует шесть типов команд:

1) V j — поставить метку, перейти к j-й строке программы.

2) X j — стереть метку, перейти к j-й строке программы.

3)

a. j — сдвинуться вправо, перейти к j-й строке программы.

4) ? j1; j2 — если в ячейке нет метки, то перейти к j1-й строке программы, иначе перейти к j2-й строке программы.

5) ! – конец программы (стоп).

У команды «стоп» отсылки нет. После запуска возможны варианты:

— работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);

— работа может закончиться командой Stop;

— работа никогда не закончится.

Статьи к прочтению:

09 — Введение в алгоритмы. Машина Тьюринга


Похожие статьи: