Сложение и вычитание вещественных чисел.

Выполнение арифметических операций над вещественными числами отличается от аналогичных операций над целыми числами.

К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.

В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

В целом оперции сложения, вычитания чисел представленных в формате с плавающей точкой выполняются в следующей последовательности:

1) Осуществляется сравнение порядков (при этом поскольку в форматах хранятся не сами порядки а смещенные порядки, как целые беззнаковые числа, то их сравнение осуществляется путем вычитания их как целых беззнаковых чисел).

2) Производится выранивание порядков числа с меньшим порядком в сторону числа с большим порядком.

3) Производится алгебраическое сложение.

4) Производится нормализация результатов.

Пример 5. Сложить двоичные нормализованные числа 0.10111•2–1 и 0.11011*210. Разность порядков слагаемых здесь равна

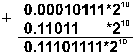
Пример 6. Выполнить вычитание двоичных нормализованных чисел 0.10101*210 и 0.11101*21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

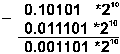
При сложении, вычитании мантисс может возникнуть нарушение нормализации (денормализация) влево на 1 разряд. Для получения нормализованного результата необходимо мантиссу сдвинуть на 1 разряд вправо, а порядок увеличить на 1.

Может возникнуть переполнение порядков. При сложении мантисс близких по модулю друг к другу, но имеющих разные знаки может возникнуть денормализация впрао на любое число разрядов вплоть до нулей. Если получились все нули, то результату присваевается машинный ноль (потеря значимости).

Если мантисса не нулевая и имеет место денормализация вправо, то для получения нормализованного результата мантисса сдвигается влево на соответствующее число разрядов (пока старшаая разрядная цифра остается равной нулю), а порядок порядок уменьшается на эту величину. В этом случае может возникнуть антипереполнение.

Задание 10.

Самостоятельно выполните в четырехбайтном формате сложение и вычитание двух вещественых чисел, выбранных из таблицы №4, предварительно переведя их в двоичную систему счисления и осуществите проверку результатов в десятичной системе.

Статьи к прочтению:

Системы счисления: Сложение, вычитание и умножение двоичных чисел. Центр онлайн-обучения «Фоксфорд»

Похожие статьи: