Сновные сведения из теории

Автор: ·

1.1. Определение машины Тьюринга

Содержательно Машина Тьюринга (МТ) как абстрактный автомат, реализующий алгоритм вычисления некоторой вычислимой функции, состоит из трех компонентов:

1. Управляющее устройство (УУ), которое может находиться в одном из состояний, образующих конечное множество 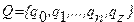— внутренний алфавит машины Тьюринга;

2. Бесконечная лента, разбитая на ячейки, в каждой из которых может быть записан один из символов конечного алфавита 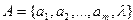— внешний алфавит машины Тьюринга;

3. Устройство обращения к ленте — считывающая и записывающая головка, которая в текущий момент времени считывает или записывает значение одной (текущей) ячейки ленты;

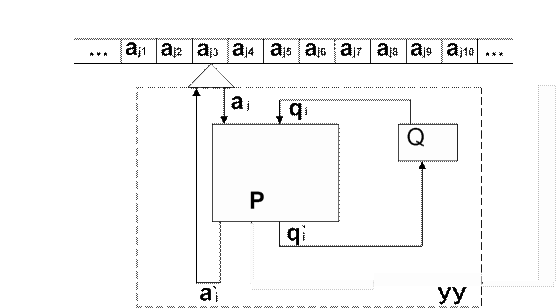
Рисунок 1 Схема машины Тьюринга

1.2. Принцип функционирования машины Тьюринга

В каждый дискретный момент времени (момент работы машины Тьюринга)

  • Машина находится в одном из внутренних состояний;
  • Головка обозревает одну из ячеек ленты.

При переходе к следующему такту выполняются следующие действия:

  • Машина переходит в некоторое другое состояние (или остается в текущем состоянии).
  • В обозреваемую ячейку записывается некоторый символ (или содержимое ячейки не изменяется).
  • Головка передвигается на одну ячейку вправо(R), влево(L), или остается в том же положении (E).

<p>Шаг машины представляет собой считывание символа из обозреваемой ячейки; определение состояния, в котором находится управляющее устройство и в зависимости от этого перевод управляющего устройства в новое состояние, запись на ленту нового символа и, перемещение головки вправо (R) или влево (L) или оставление головки на месте (E).

Формальная команда машины Тьюринга может быть задана в следующем виде:

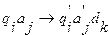(1)

где:

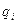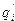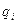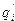
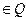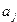и — состояние машины до и после выполнения команды и ;

и 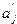— обозреваемый символ в ячейке до и после выполнения
команды 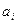и ;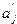

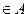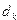– символ, указывающий направление сдвига головки .

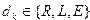Совокупность команд (программа) образует множество P;

Среди символов внутреннего алфавита машины Тьюринга Q можно выделить:

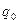  • — начальное состояние МТ,
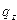  • — конечное состояние МТ

Машина начинает функционировать, находясь в состоянии 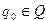; и заканчивает (останавливается) в состоянии .

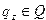Среди символов внешнего алфавита машины Тьюринга выделяют символ 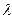– пустой символ, 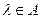. Запись символа 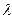в ячейку ленты означает очистку этой ячейки.

Полным состоянием или конфигурацией машины Тьюринга называется такая совокупность символов из A и Q, которая однозначно определяет дальнейшее поведение машины.

Полное состояние (конфигурация) имеет следующий вид:

,

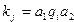где:

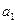— слово, находящееся на ленте слева от головки;

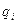— текущее внутренне состояние ;

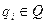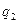— слово, образованное символом, обозреваемым головкой и всеми символами справа от него.

Стандартной начальной конфигурацией называется конфигурация вида

,

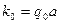т.е. конфигурацию, при которой головка обозревает крайний левый символ записанного на ленте слова a, а внутренними состоянием является .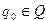

Стандартной конечной конфигурацией называется конфигурация следующего вида:

,

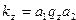где 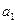и 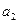любые слова во внешнем алфавите А (в т.ч. и пустые). Внутренним состоянием является заключительное состояние .

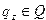Машина Тьюринга – абстрактный автомат задаваемый кортежем следующего вида:

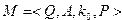
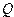– внутренний алфавит;

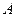– внешний алфавит;

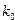– начальная конфигурация;

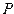– совокупность команд машины.

1.3. Способы задания МТ

Задать вычислительный алгоритм в алгоритмической системе Тьюринга — это значит задать поведение МТ по любым внешним (входным) данным.

Поведение (или функционирование МТ) как и любой другой вычислительной машины (неабстрактной) может быть задано программой, составленной как минимум 3 различными способами:

1) Совокупностью команд МТ, прямым их перечислением;

2) Таблицей переходов МТ;

3) Блок-схемой или диаграммой переходов МТ.

Рассмотрим перечисленные способы на примере:

M = ,

где

Q = { q0 , q1 , q2 , q z } ,

A = {a, b, c, ?},

K0 = q0 a b c ?.

1) Совокупность команд:

P = {q0 aq1 ? R ; q1 bq2 ? R ; q2 cq z ? E }

2) Таблица переходов:

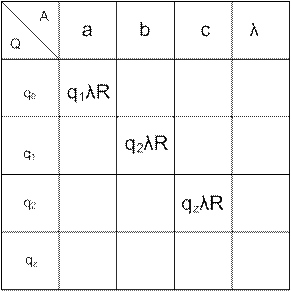
3) Диаграмма переходов:

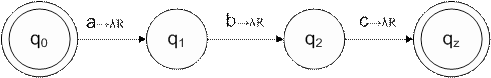
1.4. Вычисления на МТ

Рассмотрим, каким образом производятся вычисления на МТ.

В общем случае внешний алфавит (A) представляет собой

,

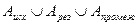где

Aисх – алфавит, на котором могут быть записаны исходные слова на ленте перед началом работы МТ,

Aрез – множество символов (алфавит), на котором могут быть записаны все слова на ленте после остановки МТ,

Aпромеж – алфавит, символы которого могут появляться во время функционирования МТ.

Замечание: будем рассматривать простейший случай, когда все алфавиты совпадают.

В соответствии с определением стандартной начальной конфигурации (K0) ко всякой незаключительной конфигурации (Ki) применима некоторая команда МТ. После такого применения МТ переходит в новое полное состояние (или конфигурацию) Ki+1 . Этот переход принято обозначать

.

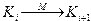Если для некоторых Ki , Kj существует такая последовательность конфигураций

,

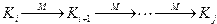то это принято обозначать

.

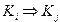Определение:

Дана f-функция, отображающая множество слов из алфавита 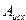во множество слов из 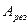. Машина Тьюринга М вычисляет (правильно) функцию f, если:

1) f(V)=W и 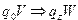, для 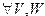– множество слов в алфавите 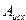и 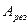соответственно.

2) Существует V такое, что f(V) – не определено. Тогда и МТ, запущенная в стандартной начальной конфигурации q0 V, работает бесконечно долго или зацикливается.

Определение:

Если для f существует МТ М, которая ее вычисляет (правильно), то функция f называется (правильно) вычислимой по Тьюрингу.

Замечание: Две МТ, M1 и M2 , с одинаковыми алфавитами 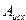являются эквивалентными, если они правильно вычисляют одну и ту же функцию.

1.5. Примеры МТ

Построить МТ, которая бы умножала два натуральных числа.

Условимся обозначать натуральное число a словом, состоящим из такого количества единиц, количество которых равно численному значению a, а разделительный символ между числами будем обозначать «*».

Построить МТ для

1a * 1b 1a+b .

, , , .

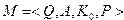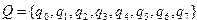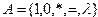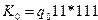Решение:

P = { , , , , , , , , , , , , , , , , }.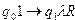

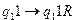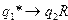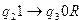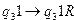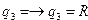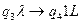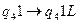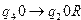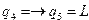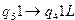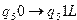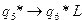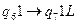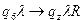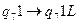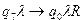1.6. Тезис Тьюринга

Для каждой ли вычислимой функции можно построить реализующий её на МТ алгоритм?

Ответом служит тезис Тьюринга: «Всякий алгоритм может быть реализован на МТ». Доказательства у этого утверждения нет, и не может быть, поскольку само понятие алгоритма является неточным.

Подтверждением тезиса Тьюринга могут служить следующие обстоятельства (неформальные):

— практика создания программ для МТ по всем вычислительным функциям;

— совокупность описания алгоритма в любой алгоритмической системе к МТ.

Этот тезис позволяет утверждать, что если невозможно создать МТ для вычисления какой-либо функции, то алгоритма вычисления этой функции не существует вообще!

В частности, это относится к:

  • решению проблемы остановки для произвольной МТ
  • проблеме определения выводимости в любой теории и т.д.
  • проблеме существования М-транслятора: любой программы на алгоритмическом языке , которая определяет зацикливание

Проблема остановки для произвольной МТ:

— по некоторому алгоритму (?? А и Д ? ) определить, существует ли результат вычислений по алгоритму А?

— построить МТ М0 так, что любые М и любые и Д?

T0(T,?) = «Истина», если М – останавливается.

T0(T,?) = «Ложь», если М — не останавливается.

Статьи к прочтению:

Сведение-просто! Урок 1: Основы теории сведения.


Похожие статьи:

Метки:

Читайте также:

Последняя инфа: