Тема 3. основы дискретной математики.
Цель темы – ознакомиться с основами алгебры логики, функциями отношениями и множествами.
План лекции
1. Функции, отношения, множества
2. Основы логики
Литература 5,10,11,29,34
Функции, отношения, множества
Понятия «множества», «отношения», «функции» и близкие к ним составляют основной словарь дискретной математики. Основоположником теории множеств является немецкий математик Г. Кантор.
Множеством называется совокупность однотипных объектов, обладающих общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты.
Следующие совокупности объектов являются множествами: множество товаров в магазине, множество натуральных чисел, множество студентов, множество букв алфавита.
Всякое множество состоит из элементов. Множества обозначают заглавными буквами латинского алфавита, например А, В, С, а элементы — маленькими буквами, например, а, Ь, с.
Пример 1.1.
Множества могут быть конечными (т.е. состоящими из конечного числа элементов) и бесконечными. Число элементов в конечном множестве называется мощностью множества. Множество и его элементы обозначаются следующим образом:
А = {а1, а2,а3 } — множество, состоящее из трех элементов;
А = {а1, а2, … }- множество, состоящее из бесконечного числа элементов.
Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент а и множество А, состоящее из единственного элемента а.
Пример1.2.
Множество А = {1,2, 7} состоит из трех элементов 1,2,7.
Множество Х={1, 3, 5, 8}. Мощность |Х|= 4.
Если элемент а принадлежит множеству А, это записывается следующим образом: 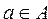 . Если элемент а не принадлежит множеству А, то записывают так:
. Если элемент а не принадлежит множеству А, то записывают так: 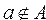
Пример 1.3.
Пусть А1 — множество нечетных чисел, А2 — множество целых чисел, а = 4.
Тогда
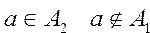
Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А— В.
Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В, и записывают А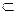 В. Отметим, что по определению само множество А является своим подмножеством, т.е. А
В. Отметим, что по определению само множество А является своим подмножеством, т.е. А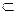 А.
А.
Если А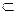 В и В
В и В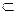 А, то по ранее введенному определению А = В.
А, то по ранее введенному определению А = В.
Если А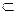 В и
В и 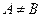 , то A есть собственное подмножество В, A В. Если А не является собственным подмножеством В, то записывают A
, то A есть собственное подмножество В, A В. Если А не является собственным подмножеством В, то записывают A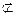 В.
В.
Пример 1.4.
Пусть А — множество четных чисел, В — множество целых чисел, С -множество нечетных чисел. Тогда
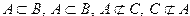
Не надо смешивать отношение принадлежности ( 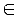 ) и отношение включения (
) и отношение включения (  ).
).
Пример 1.5.
Пусть A = {2} — множество, состоящее из одного элемента, В = {{2}, {4}} — множество, состоящее из двух элементов, каждое из которых является одноэлементным множеством. Тогда имеют место следующие соотношения:
2 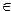 {2};
{2};
{2} 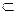 {{2}, {4}};
{{2}, {4}};
2 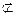 {{2}, {4}}.
{{2}, {4}}.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается O. Принято считать, что пустое множество является подмножеством любого множества, O 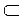 А, где А — любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.
А, где А — любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.
Множество всех подмножеств данного множества А называется множеством-степенью и обозначается Р(А). Множество Р(А) состоит из 2n элементов.
Пример 1.6.
Пусть множество A = {1, 2} состоит из двух элементов 1, 2. Тогда множество Р(А) включает в себя пустое множество O, два одноэлементных множества {1} и {2} и само множество А = {1,2}, т.е.
P(A)={O,{1},{2},{1,2}}.
Мы видим, что множество Р(А) состоит из четырех элементов (4 = 22).
Статьи к прочтению:
Дискретный мир
Похожие статьи:
-
Тема: основы программирования (с помощью пакета mаtlab).
Вопросы к экзамену по информатике. 1 семестр 2012 года. Специальность: СУ-21. Теория Основные понятия информатики. Меры и единицы измерения информации….
-
Тема 1 основы построения автоматизированных информационных систем бухгалтерского учета
Понятие автоматизированной информационной системы бухгалтерского учета, характеристика информации, информационный процесс, обеспечивающие компоненты,…
