Теоретическая часть. состав машины поста
Машина Поста состоит из ленты и каретки (называемой также считывающей и записывающей головкой). Лента бесконечна и разделена на секции одинакового размера — ячейки.
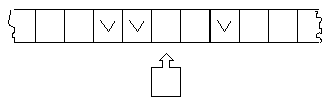
Рис. 1. В каждый момент времени каретка указывает на одну из ячеек
В каждой ячейке ленты может быть либо ничего не записано, либо стоять метка V. Информация о том, какие ячейки пусты, а какие содержат метки, образует состояние ленты. Иными словами, состояние ленты — это распределение меток по ячейкам. Состояние ленты меняется в процессе работы машины. Заметим, что наличие метки в ячейке можно интерпретировать как “1”, а отсутствие — “0”. Такое двоичное представление информации подобно представлению, используемому практически во всех современных ЭВМ.
Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной ячейки ленты; говорят, что каретка обозревает одну ячейку. За единицу времени каретка может совершить одно из трех действий: стереть метку, поставить метку, совершить движение на соседнюю ячейку. Состояние машины Поста складывается из состояния ленты и положения каретки.
Действия каретки подчинены программе, состоящей из перенумерованного набора команд (команды можно представлять как строки программы). Команды бывают шести типов:
1. записать 1 (метку), перейти к i-й строке программы;
2. записать 0 (стереть метку), перейти к i-й строке программы;
3. сдвиг влево, перейти к i-й строке программы;
4. сдвиг вправо, перейти к i-й строке программы;
5. останов;
6. если 0, то перейти к i, иначе перейти к j.
Приведем список недопустимых действий, ведущих к аварийной остановке машины:
- попытка записать 1 (метку) в заполненную ячейку;
- попытка стереть метку в пустой ячейке;
- бесконечное выполнение (вообще говоря, это трудно назвать аварийным остановом, но бессмысленное повторение одних и тех же действий — зацикливание — ничуть не лучше вышеперечисленного).
Машина Поста, несмотря на внешнюю простоту, может производить различные вычисления, для чего надо задать начальное состояние каретки и программу, которая эти вычисления сделает. Машиной эта математическая конструкция названа потому, что при ее построении используются некоторые понятия реальных машин (ячейка памяти, команда и др.). Условимся каждый шаг программы обозначать номером. Команды машины будем обозначать следующим образом:

Будем говорить, что мы можем применить программу к текущему состоянию машины Поста, если выполнение программы не приведет к зацикливанию, т.е. рано или поздно мы выполним команду останов.
Пример программы, которая не применима ни к одному состоянию машины Поста:
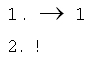
Рассмотрим задачу для машины Поста и ее решение.
Задача.На ленте проставлена метка в одной-единственной ячейке. Каретка стоит на некотором расстоянии левее этой ячейки. Необходимо подвести каретку к ячейке, стереть метку и остановить каретку слева от этой ячейки.
Решение. Сначала попробуем описать алгоритм обычным языком. Поскольку нам известно, что каретка стоит напротив пустой ячейки, но неизвестно, сколько шагов нужно совершить до пустой ячейки, мы можем сразу сделать шаг вправо; проверить, заполнена ли ячейка; если она пустая, то повторять эти действия до тех пор, пока не наткнемся на заполненную ячейку. Как только мы ее найдем, мы выполним операцию стирания, после чего нужно будет лишь сместить каретку влево и остановить выполнение программы.
Программа для машины Поста:

Практическая часть практикума “Машина Поста”
Все задачи практикума сгруппированы по темам. Начинать знакомство с машиной Поста рекомендуется с первой темы “Применимость программ. Определение результата выполнения программ”.
Пояснения к условиям задач
1) В задачах под массивом понимается последовательность подряд идущих меток, ограниченная пустыми ячейками.
2) Если в задаче говорится, что на ленте задано число в унарной системе, то имеется в виду, что натуральное число n закодировано с помощью массива длины n.
3) В задачах при описании начального состояния ленты будем указывать то, что записано начиная с самой левой непустой ячейки и заканчивая самой правой непустой ячейкой. При этом будем использовать следующие обозначения: n подряд идущих меток будем обозначать 1n, а m пустых ячеек — 0m. При обозначении одной заполненной или пустой ячейки будем писать просто 1 или 0, соответственно.
К примеру, запись “12012” будет соответствовать записи “11011” на ленте.
4) Если не сказано ничего о местонахождении каретки в начальный момент времени, то будем считать, что каретка обозревает ячейку с самой левой меткой.
Статьи к прочтению:
- Теоретические основы организации элективного курса по информатике.
- Территориальная распространенность
Лаборатория Электротехника и основы электроники (Учебная техинка профи, учтех-профи)
Похожие статьи:
-
Программирование машины тьюринга
Машина Тьюринга — это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный…
-
Модели вычислений: машина тьюринга, расп, рам, неветвящиеся программы, деревья решений
Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом…
