Вложенные циклы в матричных задачах

Цель работы: получение практических навыков в программировании вычислительных процессов вложенной циклической структуры в матричных задачах и навыков в организации вывода информации в виде таблиц.

Задания для самостоятельной подготовки

1.1. Изучить возможности языка программирования для реализации вычислительного процесса вложенной циклической структуры в матричных задачах с известным числом повторений в цикле.

1.2. Разработать алгоритм решения в соответствии с заданием.

1.3. Подготовить тесты для проверки правильности функционирования программы.

Задания к работе

Выполнить программу на ЭВМ с использование вложенных циклов. В программе указать название работы, фамилию исполнителя, группу и номер варианта задания. На печать вывести значения вводимых исходных данных и результаты вычислений.

Варианты заданий

1. Даны целые числа 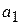, , 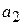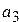. Получить целочисленную матрицу 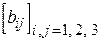, для которой .

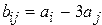2. Даны действительные числа 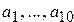, 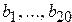. Получить действительную матрицу 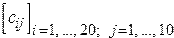, для которой .

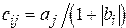3. Получить 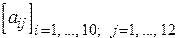— целочисленную матрицу, для которой .

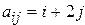4. Дано натуральное число 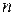. Получить действительную матрицу 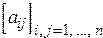, для которой .

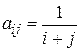5. Дана действительная квадратная матрица 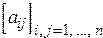. Получить две квадратные матрицы 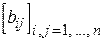, , 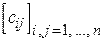для которых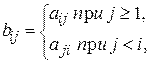

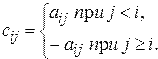
6. Получить действительную матрицу 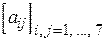, первая строка которой задается формулой 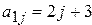( 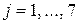), вторая строка задается формулой 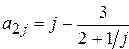( 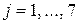), а каждая следующая строка есть сумма двух предыдущих.

7. Даны натуральные числа 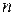, , 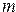действительная матрица размера 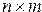. Найти среднее арифметическое для каждого из столбцов.

8. Дано натуральное число 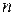. Выяснить, сколько положительных элементов содержит матрица 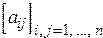, если .

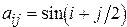9. Дана действительная матрица размера 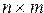, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент.

10. Дана действительная квадратная матрица порядка 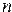. Заменить нулями все ее элементы, расположенные на главной диагонали и выше нее.

11. Дана действительная матрица размера 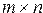. Определить числа , равные наименьшим значениям элементов строк.

12. Дана действительная матрица размера 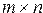. Определить числа , равные значениям средних арифметических элементов строк.

13. Дано натуральное число 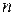. Выяснить, сколько положительных элементов содержит матрица 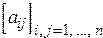, если .

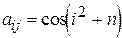14. Дано натуральное число 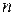, действительная матрица 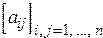. Получить последовательность из элементов главной диагонали 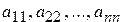, расположенных в порядке убывания.

15. Дана действительная матрица размера 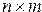. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов.

16. Дана действительная матрица размера 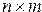. Найти значение наибольшего по модулю элемента матрицы, а также индексы всех элементов с найденным значением модуля.

17. Дана действительная матрица размера 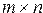. Найти сумму наибольших значений элементов ее строк.

18. Дано натуральное число 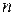. Выяснить, сколько положительных элементов содержит матрица 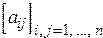, если .

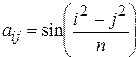19. Дана действительная матрица размера 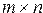. Определить числа , равные произведениям элементов строк.

20. В данной квадратной целочисленной матрице порядка 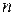указать индексы всех элементов с наименьшим значением.

21. Дана действительная матрица размера 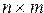. Получить последовательность , где 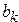— это наибольшее из значений элементов 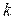-й строки.

22. Дана целочисленная квадратная матрица порядка 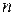. Найти номера строк, элементы каждой из которых образуют монотонную последовательность (монотонно убывающую или монотонно возрастающую).

23. Дана действительная квадратная матрица порядка 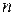. В строках с отрицательным элементом на главной диагонали найти сумму всех неотрицательных элементов.

24. Дана действительная квадратная матрица порядка 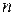. Получить целочисленную квадратную матрицу того же порядка, в которой элемент равен единице, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, и равен нулю в противном случае.

25. Дана действительная квадратная матрица порядка 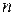. Получить 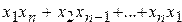, где 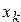— наибольшее значение элементов 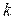-й строки данной матрицы.

ЛАБОРАТОРНАЯ РАБОТА №4

ИСПОЛЬЗОВАНИЕ ПОДПРОГРАММ

Цель работы: получение практических навыков в программировании вычислительных процессов с использованием подпрограмм.

Основы теории

Подпрограммой называют обособленную группу операторов, которую можно выполнять многократно, обращаясь к ней из различных мест программы.

Использование подпрограмм уменьшает общее количество операторов в программе и, следовательно, для размещения программы требуется меньше памяти. Время на выполнение программы при этом практически не изменяется. Использование подпрограмм улучшает структуру программы. Облегчается отладка программы, так как работа каждой подпрограммы может быть проверена по отдельности. Подпрограммами может воспользоваться не только тот, кто написал подпрограмму, но и другие лица.

Большинство машин располагает обширными библиотеками стандартных подпрограмм, которые существенно облегчают программирование реальных задач.

В Бейсике подпрограмма оформляется как группа операторов, которая должна выполняться при обращении к ней, и составляет с программой единое целое.

Обращение к подпрограмме осуществляется оператором

GOSUB N,

где N – номер строки, с которой начинается подпрограмма.

Подпрограмма размещается в последних строках, начиная с N–ой. Последним оператором, выполняемым в подпрограмме, должен быть оператор RETURN. По оператору RETURN осуществляется возврат в то место программы, из которого произошло обращение к подпрограмме, а именно к оператору, следующему за GOSUB N. Подпрограмма может содержать обращения к другим подпрограммам.

Задания к работе

Выполнить программу на ЭВМ с использование подпрограмм. В программе указать название работы, фамилию исполнителя, группу и номер варианта задания. На печать вывести значения вводимых исходных данных и результаты вычислений.

Варианты заданий

1. Даны действительные числа 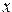, 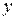. Получить

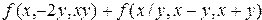, где

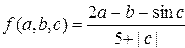2. Даны действительные числа 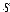, 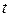. Получить

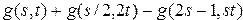, где

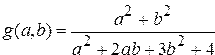3. Дано натуральное число 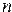, действительное число 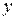. Получить

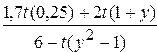, где .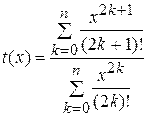

4. Даны натуральные числа 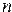, , 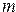, 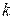целые числа , , 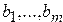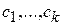. Получить

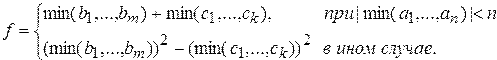
5. Даны натуральные числа 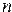, , 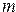, 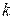целые числа , , 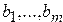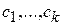. Получить

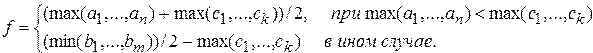
6. Даны действительные числа 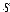, 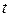. Получить

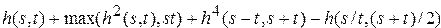, где

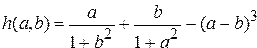7. Дано натуральное число n и действительные числа 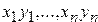. Найти периметр 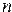-угольника, вершины которого имеют координаты .

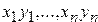8. Дано натуральное число n и действительные числа 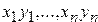. Найти площадь 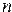-угольника, вершины которого при последовательном обходе имеют координаты .

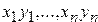9. Дано натуральное число n и действительные числа 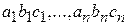. Найти сумму площадей треугольников с длинами сторон .

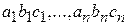10. Дано четное число 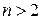. Проверить для этого числа гипотезу Гольдбаха. Согласно этой гипотезе, каждое четное 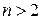, представляется в виде суммы двух простых чисел.

11. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся простыми числами.

12. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся совершенными числами.

13. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, кратные 3 и некратные 5.

14. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся квадратами четных чисел.

15. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся удвоенными нечетными числами.

16. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся полными квадратами.

17. Дана действительная матрица размера 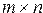. Найти сумму наименьших значений элементов ее столбцов.

18. Дана действительная матрица размера 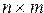, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент.

19. Дана действительная матрица размера 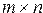. Найти сумму наименьших значений элементов ее строк.

20. Дана действительная матрица размера 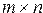. Найти сумму наибольших значений элементов ее столбцов.

21. Дана действительная матрица размера 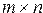. Найти сумму наименьших значений элементов ее строк.

22. Дана действительная матрица размера 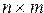, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наименьший неравный нулю элемент.

23. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся четными числами.

24. Дано натуральное число n и целые числа а1…аn. Получить все члены последовательности, являющиеся нечетными числами.

25. Даны натуральные числа 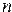, , 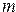, 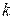целые числа , , 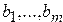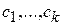. Получить

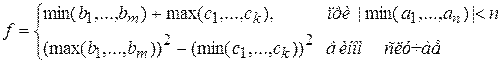
26. Даны натуральные числа 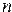, , 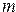, 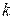целые числа , , 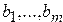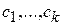. Получить

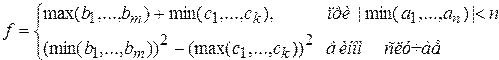
27. Даны действительные числа 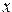, 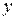. Получить

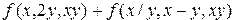, где

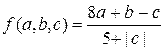28. Даны действительные числа 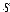, 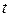. Получить

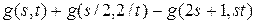, где

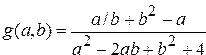29. Даны действительные числа 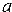, 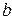. Вычислить

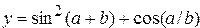
30. Даны действительные числа 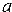, 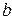. Вычислить

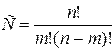
Вычисление факториала оформить в виде подпрогаммы

Примечания

В задачах данного параграфа, говоря о процедурах, подразумевается, что решающий сам выбирает подходящее средство программирования – подпрограмму, функцию или процедуру.

Статьи к прочтению:

Куда вложить 100 000 рублей?

Похожие статьи: