Задача 2. разработка алгоритма линейной структуры и его реализация в виде программы vba.
Таблица 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Вычислить высоты треугольника со сторонами a, b, c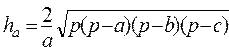 , , 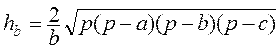 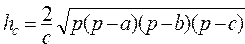 , где , где 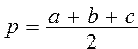 | |
Вычислить площадь поверхности и объем усеченного конуса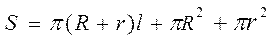 ; ; 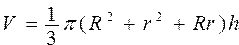 | |
Вычислить координаты центра тяжести трех материальных точек с массами m1, m2, m3 и координатами (x1,y1), (x2,y2), (x3,y3), по формулам 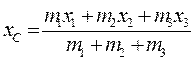 , , 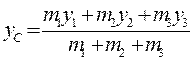 | |
Вычислить координаты точки, которая делит отрезок А1А2 в соотношении n1 : n2 по формулам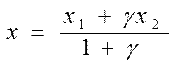 ; ; 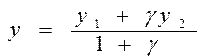 , де , де 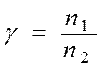 | |
Вычислить медианы треугольника со сторонами по формулам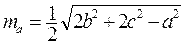 ; ; 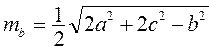 ; ; 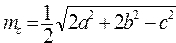 | |
Вычислить значение функции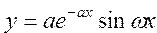 , где , где 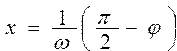 |
jIIIIIIIIIIIIПродолжение таблицы 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Вычислить угловую скорость w и центростремительное ускорение a по формулам 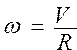 ; ; 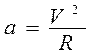 ; ; 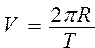 | |
Вычислить значение функции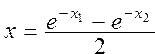 и и 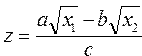 ,где ,где 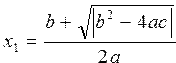 ; ;  | |
Вычислить значение функции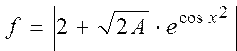 , где , где 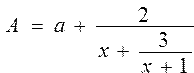 | |
Используя уравнения теплового баланса, определить удельную теплоемкость по формулам 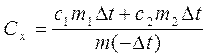 , де , де 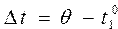 | |
Определить коэффициенты линейного b и объемного a расширения куба с размером грани l0 по формулам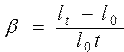 , , 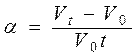 | |
Определить удельную теплоту по формуле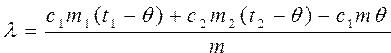 | |
Вычислить силу тяжести на полюсах, экваторе и на заданной широте ? по формулам 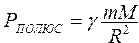 ; ;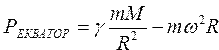 ; ; 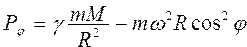 |
Продолжение таблицы 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Вычислить значения гиперболических функций (синуса, косинуса, тангенса) по формулам ; ; 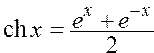 ; ;  | |
Вычислить значения гиперболических функций (арктангенса и арккотангенса) по формулам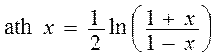 ; ; 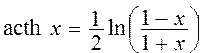 | |
Вычислить логарифм числа N по основаниям: a,b,2a+b, ab по формуле 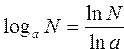 | |
Вычислить значения арксинуса, арккосинуса, арккотангенса: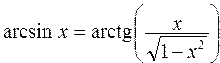 ; ; 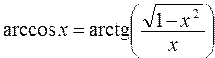 ; ;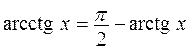 | |
Преобразовать декартовы координаты в сферические в пространстве по формулам: полярного радиуса 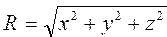 , долготы , долготы 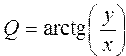 , широты , широты 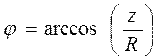 | |
Преобразовать сферические координаты (полярный радиус R, долготу f, широту Q) в декартовы координаты по формулам: 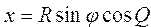 ; ; 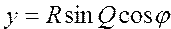 ; ; 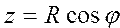 | |
Преобразовать полярные координаты в прямоугольные по формулам: 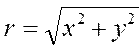 ; ; 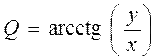 .Вычислить длину вектора D с координатами начала (x1 , y1) и конца (x2 , y2) .Вычислить длину вектора D с координатами начала (x1 , y1) и конца (x2 , y2)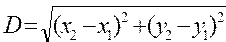 |
Продолжение таблицы 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Определить температуру сварного стыка арматурных стержней по формуле 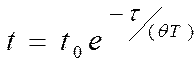 , где , где 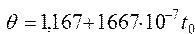 | |
Рассматривается вектор в пространстве с началом в точке (0, 0, 0) декартовой системы координат и концом в точке (X, Y, Z). Вычислить его длину D и дуги a, b, g, которые он составляет с осями координат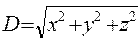 ; ;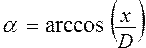 ; ; 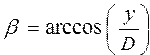 ; ; 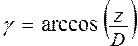 | |
Вычислить полное сопротивление Z переменного тока, напряжения UC и UL на конденсаторной катушке индуктивности по формулам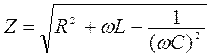 ; ; 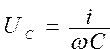 ; ; 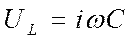 | |
Вычислить объем, площадь полной и боковой поверхности цилиндра по формулам: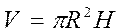 , , 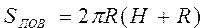 , , 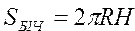 | |
Вычислить объем и площадь поверхности шара и шарового сегмента по формулам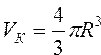 , , 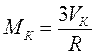 , , 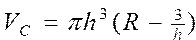 , , 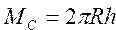 | |
Вычислить скорости V1I и V2 I, потерю энергии W в момент лобового столкновения двух тел с массами m1 и m2 по формулам  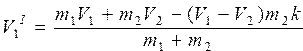 ; ;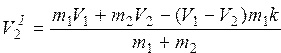 ; ;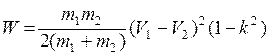 |
Продолжение таблицы 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Даны: сторона треугольника a и прилегающие к ней углы ? и ?. Определить две другие стороны b и c, угол между ними ? по формулам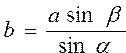 ; ; 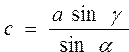 ; ;  | |
Выполнить преобразования декартовых координат на плоскости при сдвиге и повороте осей координат по формулам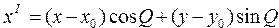 ; ;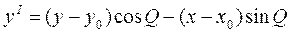 ,где xI и yI – новые координаты точки (x,y), x и y – координаты центра новой системы координат ,где xI и yI – новые координаты точки (x,y), x и y – координаты центра новой системы координат | |
Даны медианы треугольника ma , mb , mc .Определить площадь треугольника по формулам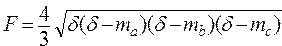 ; ; 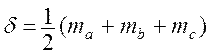 | |
Найти значения среднеарифметического температурного градиента ?tA и ?tL по формулам:, 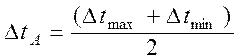 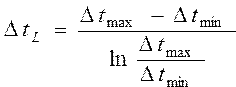 | |
Найти площадь боковой поверхности и объем правильной усеченной пирамиды по формулам: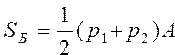 , , 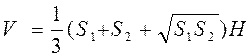 | |
Найти радиусы вписанного и описанного круга через стороны и углы треугольника по формулам: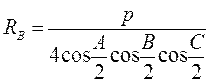 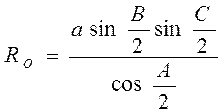 |
Продолжение таблицы 2
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Найти площадь прямолинейной трапеции, а также расстояния центра тяжести от основания a и основания b по формулам: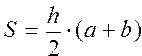 , , 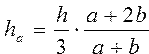 , , 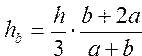 | |
Найти сопротивление однородных проводников при постоянной и переменной температуре по формулам: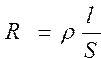 , , 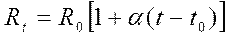 | |
Найти фазовый сдвиг и мощность переменного тока по формулам , , 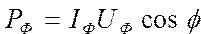 | |
Записать формулы умножения и деления двух комплексных чисел m и n: 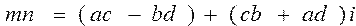 , ,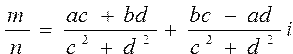 | |
Найти фокусное расстояние двояковыпуклой линзы и расстояние светящейся точки до линзы по формулам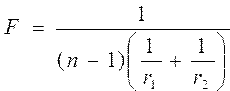  | |
Вычислить сумму всех членов арифметической и геометрической прогрессии по формулам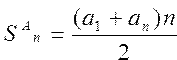 , , 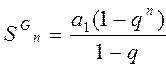 | |
Вычислить энергию связи атомного ядрапо формулам 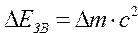 ; ; 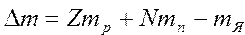 |
Продолжение таблицы 2
IIIIIIII IIIIII
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Вычислить значения тригонометрических функций для кратных аргументов по формулам: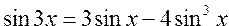 ; ; 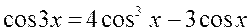 ; ;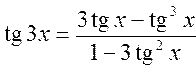 ; ; 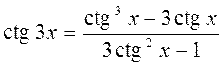 | |
Вычислить энергию и скорость молекул по формулам ; ; 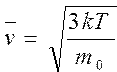 | |
Вычислить площадь поверхности шарового сегмента, сектора и слоя по формулам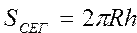 , , 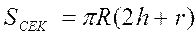 , , 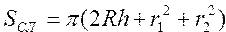 | |
Вычислить площадь боковой поверхности и объем правильной усеченной пирамиды по формулам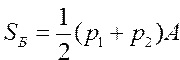 , , 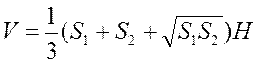 | |
Вычислить значения логарифмов по формулам, используя свойства логарифмов: 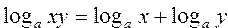 , ,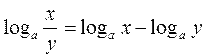 , , 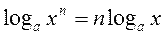 | |
Вычислить значения производных тригонометрических функций по формулам: 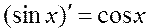 ; ; 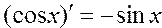 ; ;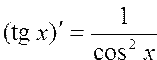 ; ; 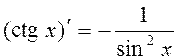 | |
Вычислить значения тригонометрических функций для кратных аргументов по формулам: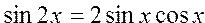 ; ; 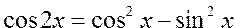 ; ;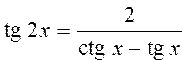 ; ; 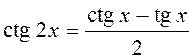 |
Продолжение таблицы 2
IIIIIIIIIIIIIII
| № п.п. | Задача 2 Построить алгоритм линейной структуры и написать программу |
Вычислить объем шарового сегмента, сектора и слоя по формулам 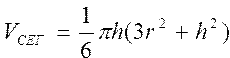 , , 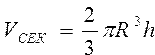 , ,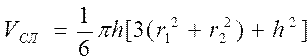 | |
Вычислить в соответствии с релятивистскими законами скорость, импульс и массу по формулам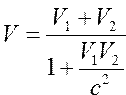 ; ; 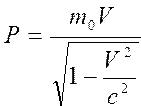 ; ;  | |
Вычислить радиус кривизны и длину параболы от вершины О до точки с координатами (x, y) по формулам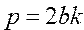 ; ; 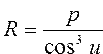 ; ; 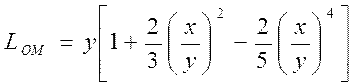 | |
Вычислить корни кубического уравнения по формулам: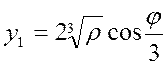 ; ; 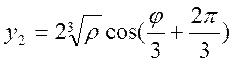 ; ;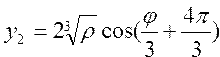 |
I
IIIIIIII
Статьи к прочтению:
Тема 2 Программирование линейных и разветвляющихся структур алгоритмов
Похожие статьи:
-
Задача 3 а. алгоритм разветвляющейся структуры
Таблица 3 а № п.п. Задача 3 А Построить алгоритм разветвляющейся структурыи написать программу вычисления значения функции , где , где , где , x = 2,8 ,…
-
Алгоритм линейной структуры (следование) – алгоритм, в котором все действия выполняются последовательно друг за другом. Такой порядок выполнения действий…
