Алфавитный подход к измерению информации.

Лабораторная работа №1

«Измерение информации»

В информатике используются различные подходы к измерению информации:

Количество информации- это мера уменьшения неопределенности.

Содержательный подход к измерению информации.

Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными Информация — знания человека ? сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику).

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Количество информации i, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, можно определить из формулы Хартли:

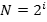
Данная формула является показательным уравнением относительно неизвестного i. Из математики известно, что решение такого уравнения имеет вид:

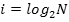
Если N равно целой степени двойки (2,4,8,16 и т. д.), то такое уравнение можно решить «в уме».

Пример:

Шахматная доска состоит из 64 полей: 8 столбцов на 8 строк. Какое количество бит несет сообщение о выборе одного шахматного поля?

Решение.

Поскольку выбор любой из 64 клеток равновероятен, то количество бит находится из формулы:

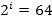
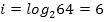
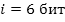
Алфавитный подход к измерению информации.

Алфавит -множество используемых символов в языке.

Обычно под алфавитом понимают не только буквы, но и цифры, знаки препинания и пробел.

Мощность алфавита(N)-количество символов, используемых в алфавите.

Например, мощность алфавита из русских букв равна 32 (буква ё обычно не используется).

Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле Хартли:

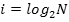
где N — мощность алфавита.

Формула Хартли задает связь между количеством возможных событий N и количеством информацииi:

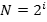
Из базового курса информатики известно, что в компьютерах используется двоичное кодирование информации. Для двоичного представления текстов в компьютере чаще всего используется равномерный восьмиразрядный код. С его помощью можно закодировать алфавит из 256 символов, поскольку 256=28.

В стандартную кодовую таблицу (например, ASCII) помещаются все необходимые символы: английские и русские прописные и строчные буквы, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.

В двоичном коде один двоичный разряд несет одну единицу информации, которая называется 1 бит.

Например, в 2-символьном алфавите каждый символ «весит» 1 бит (log22=1); в 4-символьном алфавите каждый символ несет 2 бита информации (log24=2); в 8-символьном — 3 бита (log28=3) и т. д.

Один символ из алфавита мощностью 256 (28) несет в тексте 8 битов информации. Такое количество информации называется байтом.

1байт=8битов

Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста.

Для измерения информации используются и более крупные единицы:

Название единицы измерения	Численная величина в байтах	Точное количество байтов
Килобайт (Кбайт)		1024 байт
Мегабайт (Мбайт)		1024 килобайт1 048 576 байт
Гигабайт(Гбайт)		1024 мегабайт1 073 741 824 байт
Терабайт (Тбайт)		1024 гигабайт099 511 627 776 байт
Петабайт (Пбайт)		1024 терабайт1 125 899 906 842 624 байт
Эксабайт (Эбайт)		1024 петабайт1 152 921 504 606 846 976 байт
Зеттабайт(Збайт)		1024 эксабайт1 180 591 620 717 411 303 424байт
Йоттабайт(Йбайт)		1024 зеттабайт1208925819614629174706176 байт

Если весь текст состоит из K символов, то при алфавитном подходе объём V содержащейся в нем информации равен:

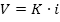
где i — информационный вес одного символа в используемом алфавите.

Зная, что i=log2N, данную выше формулу можно представить в другом виде:

если количество символов алфавита равно N, а количество символов в записи сообщения — K, то информационный объем V данного сообщения вычисляется по формуле:

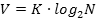
При алфавитном подходе к измерению информации информационный объем текста зависит только от размера текста и от мощности алфавита, а не от содержания. Поэтому нельзя сравнивать информационные объемы текстов, написанных на разных языках, по размеру текста.

Пример:

Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения:Белеет Парус Одинокий В Тумане Моря Голубом!

Решение.

Так как в предложении 44 символа (считая знаки препинания и пробелы), то информационный объем вычисляется по формуле:

V=44?1 байт=44 байта=44?8 бит=352 бита

Статьи к прочтению:

АЛФАВИТНЫЙ ДРАФТ ЗАРЕШАЛ

Похожие статьи: