Алгоритм метода бокса-уилсона.

1. В центре факторного пространства проводится ПФЭ (ДФЭ) и строится линейная регрессионная модель с дальнейшей целью вычисления градиента:

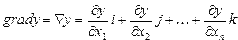, (1)

где i, j,…,k – единичные векторы в направлении координатных осей факторного пространства.

При этом результаты эксперимента подвергаются статистическому анализу, который заключается в следующем:

а) проверка воспроизводимости эксперимента;

б) проверка значимости коэффициентов линейной модели;

в) проверка адекватности линейной модели.

2. Вычисляются произведения bj?xj, среди них находится max{bj?xj}=bб?xб.

3. Для базового фактора выбирается величина шага крутого восхождения hб. Этот выбор производится на основании имеющейся априорной информации с учетом опыта исследователя, технологических соображений или других критериев. Относительно выбора шага можно заметить, что слишком малый шаг потребует значительного числа опытов при движении к оптимуму, а большой шаг создает опасность проскакивания области оптимума.

4. Определяются приращения по остальным переменным

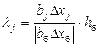. (2)

5. Проводятся «мысленные опыты», которые заключаются в вычислении предсказанных значений целевой функции (по регрессионной модели) в определенных точках факторного пространства y(x1, x2, …, xn). Для этого независимые переменные линейной модели изменяются с учетом ?j вдоль направления вектора grady, полученного в пункте 1. В результате получаем последовательность значений откликов y(X0), y(X1), y(X2), …, y(Xi) …

6. «Мысленные опыты» продолжаются до тех пор, пока выполняется неравенство y(Xi) y(Xi+1).

7. Некоторые из «мысленных опытов» (обычно через каждые 2-3 «мысленных шага») реализуются в виде эксперимента один раз. Для проверки соответствия «мысленных опытов» и реальности.

8. Точка X*, где в реальном опыте получено максимальное значение целевой функции, принимается за новую начальную точку нового цикла крутого восхождения. В зависимости от крутизны поверхности отклика приращения ?j могут быть различны в каждом цикле крутого восхождения. При приближении к экстремуму приращения должны уменьшаться.

9. Поиск прекращается, когда градиент равен нулю, т.е. все коэффициенты регрессионной модели bj оказались незначимыми.

3. Индивидуальные задания для определения оптимума отклика системы массового обслуживания на основании имитационного эксперимента.

Объектом исследования является узел компьютерной сети (УКС). Узел сети представляет собой K-процессорное устройство с общей буферной памятью известной емкости. УКС предполагает бесприоритетную дисциплину обслуживания заданий (FIFO). Функциональным назначением устройства является обработка и дальнейшая передача по сети текстовых или иных данных, которые поступают на его вход пакетами с интенсивностью ?. Данные обрабатываются каким-либо процессором с интенсивностью ?. По окончанию обработки пакет удаляется из узла. Если в момент поступления пакета процессоры заняты – пакет помещается в буферную память заданного объема — m. При полном заполнении памяти пакет, поступающий на вход УКС, получает отказ в обслуживании. . Структурная модель УКС изображена на рисунке 5.

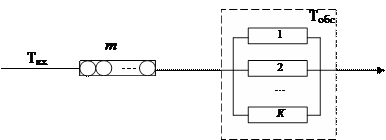Рисунок 5 — Структурная схема узла компьютерной сети.

Узел сети может быть представлен моделью системы массового обслуживания (СМО) типа M/M/К/m с отказами в обслуживании, которые происходят в результате переполнения буферной памяти [2]. Входящий поток заявок и поток обслуживания – простейшие с параметрами ? и ? соответственно.

В ходе исследования необходимо определить значения параметров СМО ? и ?, при которых заданные критерии эффективности функционирования СМО достигают своих оптимальных значений.В качестве таких критериев используются:

— вероятность отказа заданию в обслуживании

Pотк(?, ?)min;

— коэффициент использования вычислительного устройства УКС

Kи(?, ?)max;

— среднее время пребывания задания в УКС

Ts(?, ?)min.

Интенсивности входного потока заданий и потока обслуживания изменяются в заданных пределах: 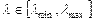и .

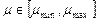Задание выполняется в ходе курсового проектирования.

Варианты типовых индивидуальных заданий представлены в Приложении 1. Номер варианта выбирается в соответствии с номером студента в списке группы.

Студент, по согласованию с преподавателем, может выполнять планирование экстремального эксперимента в рамках курсового проектирования для своего варианта.

Для выполнения задания необходимо:

1. Построить имитационную модель СМО согласно выбранному варианту [3,4].

2. В факторном пространстве выбрать центр эксперимента и определить интервалы варьирования каждого из факторов [5].

3. Провести планирование ПФЭ типа 2k [5].

4. По результатам имитационного эксперимента построить линейную регрессионную модель, определяющую зависимость функции отклика СМО от варьируемых факторов (параметров оптимизации) [5].

5. Осуществить переход к натуральным значениям факторов регрессионной модели и на основании вычисления градиента функции отклика СМО определить направление поиска оптимума функции.

6. В соответствии с алгоритмом метода Бокса-Уилсона определить оптимальные значения факторов (параметров оптимизации) функции.

7. Если тема курсовой работы предполагает исследование характера поверхности отклика в окрестности оптимума, построить квадратичную регрессионную модель на основе центральных композиционных планов [6].

4. СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ задания

1. Постановка задачи.

2. Имитационная модель УКС.

3. Матрица планирования эксперимента.

4. Анализ воспроизводимости эксперимента.

5. Анализ значимости коэффициентов линейной регрессионной модели.

6. Анализ адекватности модели.

7. Представление модели в натуральных значениях переменных. и выбор направления движения к оптимуму.

8. Анализ построенной регрессионной модели. .

2. Реализация экспериментов и процедур в соответствии с алгоритмом Бокса-Уилсона.

3. Процесс построения квадратичной регрессионной модели (если задание выполняется).

4. Анализ результатов и выводы.

5. Пример выполнения задания

Постановка задачи.

Объектом исследования является вычислительная система, которая может быть представлена многофазной Q-схемой [3]. Входной поток заявок — простейший с интенсивностью ? заданий в ед.вр. Производительность каждого из процессоров распределена экспоненциально с интенсивностью ? заданий в ед.вр. На основании проведения имитационных экспериментов необходимо определить значения параметров ? и ?, при которых среднее количество обработанных заданий 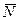вычислительной системой в течение заданного периода времени T будет максимальным.

Статьи к прочтению:

\

Похожие статьи: