Численные методы решения уравнений

Довольно часто на практике приходится решать уравнения вида:

F(x) = 0, (1),
где функция F(x) определена и непрерывна на некотором конечном или бесконечном интервале axb.

Всякое значение такое, что F(x) º 0, называется корнем уравнения, а нахождение этого значения и есть решение уравнения.

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Поэтому важное значение приобрели численные методы, позволяющие найти приближенное значение корня. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ.

Существует множество численных методов. Рассмотрим только три из них:

метод итераций;
метод Ньютона;
метод половинного деления.

Метод итераций

Представим уравнение F(x) = 0 в виде:

x = f(x). (2)

Это уравнение получается выделением x из уравнения F(x) и переносом того, что осталось, т.е. f(x), в левую часть уравнения. Иначе можно получить уравнение (2) следующим способом: левую и правую часть уравнения (1) умножить на произвольную константу l и прибавить к левой и правой части х, т.е. получаем уравнение вида:

х = х + lF(x), (3)

где f(x) = х + lF(x).

На заданном отрезке [a; b] выберем точку х0 – нулевое приближение – и найдем

х1 = f(x0),

потом найдем:

х2 = f(x1),

и т.д.

Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:

хn = f(xn-1) n = 1,2,3….. .

Этот процесс называется методом итераций.

Если на отрезке [a; b] выполнено условие:

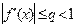то процесс итераций сходится, т.е.

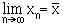
Процесс итераций продолжается до тех пор, пока

|xn — xn-1| 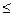e,

где – заданная абсолютная погрешность корня х. При этом будет выполняться:

|`x — xn| 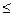e.

Метод Ньютона

Пусть уравнение F(x) = 0 имеет один корень на отрезке [a; b], причем F¢(x) и F?(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a; b].

Выберем на отрезке[a; b] произвольную точку х0 – нулевое приближение. Затем найдем:

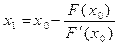потом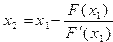

Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел xn по формуле:

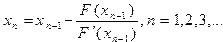
Этот процесс называется методом Ньютона.

Процесс вычисления продолжается до тех пор, пока не будет выполнено условие:

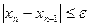
Точку х0 необходимо выбирать так, чтобы выполнялось условие:

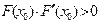иначе метод не будет сходиться.

Метод половинного деления

Пусть уравнение F(x) = 0 имеет один корень на отрезке [a;b]. Функция F(x) непрерывна на отрезке [a; b].

Метод половинного деления заключается в следующем:

Сначала выбираем начальное приближение, деля отрезок пополам, т.е.

х0 = (a+b)/2.

Если F(x)=0, то x0 является корнем уравнения. Если F(x) 0, то выбираем тот из отрезков, на концах которого функция имеет противоположные знаки. Полученный отрезок снова делим пополам и выполняем действия сначала и т.д.

Процесс деления отрезка продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданного числа e.

Постановка задачи

1. Написать функцию с умалчиваемыми параметрами в соответствии с вариантом, продемонстрировать различные способы вызова функции:

с параметрами заданными явно,
с опущенными параметрами
часть параметров задана явно, а часть опущена.

2. Написать функцию с переменным числом параметров в соответствии с вариантом, продемонстрировать вызов функции с различным числом параметров.

3. Написать перегруженные функции в соответствии с вариантом. Написать демонстрационную программу для вызова этих функций.

4. Написать шаблон функций вместо перегруженных функций из задания 3. Написать демонстрационную программу для вызова этих функций. списка параметров

5. Решить уравнение указанным в варианте методом. Уравнение передать в функцию как параметр с помощью указателя.

Варианты

№варианта	Функция с умалчиваемыми параметрами	Функция с переменным числом параметров	Перегруженные функции и шаблон функции	Передача функции как параметра другой функции с помощью указателя
	Печать фамилии, имени и отчества	Минимальный элемент в списке параметров	Среднее арифметическое массива	Метод итераций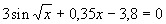Отрезок, содержащий корень: [2;3]Точное значение: 2,2985
	Печать фамилии, имени и возраста	Максимальный элемент в списке параметров	Количество отрицательных элементов в массиве	Метод Ньютона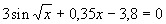Отрезок, содержащий корень: [2;3]Точное значение: 2,2985
	Печать фамилии, курса и группы	Количество четных элементов в списке параметров	Максимальный элемент в массиве	Метод половинного деления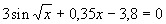Отрезок, содержащий корень: [2;3]Точное значение: 2,2985
	Печать фамилии, имени и рейтинга	Среднее арифметическое элементов в списке параметров	Минимальный элемент в массиве	Метод итераций0,25×3 + x — 1,2502 = 0Отрезок, содержащий корень: [0;2]Точное значение: 1,0001
	Печать фамилии, курса и рейтинга	Максимальный из элементов в списке параметров, стоящих на четных местах	Сортировка массива методом простого обмена	Метод Ньютона0,25×3 + x — 1,2502 = 0Отрезок, содержащий корень: [0;2]Точное значение: 1,0001
	Печать фамилии, адреса и возраста	Максимальный из элементов в списке параметров, стоящих на нечетных местах	Сортировка массива методом простого выбора	Метод половинного деления0,25×3 + x — 1,2502 = 0Отрезок, содержащий корень: [0;2]Точное значение: 1,0001
	Печать названия экзамена, количества сдающих и среднего балла	Минимальный из элементов в списке параметров, стоящих на четных местах	Сортировка массива методом простого включения	Метод итерацийОтрезок, содержащий корень: [0;0,85]Точное значение: 0,2624
	Печать названия экзамена, даты экзамена и среднего балла	Минимальный из элементов в списке параметров, стоящих на нечетных местах	Поиск заданного элемента в массиве	Метод НьютонаОтрезок, содержащий корень: [0;0,85]Точное значение: 0,2624
	Печать координат точки	Среднее арифметическое из элементов в списке параметров, стоящих на четных местах	Поиск заданного элемента в отсортированном массиве	Метод половинного деленияОтрезок, содержащий корень: [0;0,85]Точное значение: 0,2624
	Вычисление и печать расстояния от точки с координатами x1,y1 до центра координат	Среднее арифметическое из элементов в списке параметров, стоящих на нечетных местах	Удаление элемента с заданным номером из динамического массива	Метод итераций0,1×2 — x ln x = 0Отрезок, содержащий корень: [1;2]Точное значение: 1,1183
	Вычисление и печать расстояния от точки с координатами x1,y1 до точки с координатами x2,y2	Минимальный элемент в списке параметров	Удаление элемента с заданным ключом из динамического массива	Метод Ньютона0,1×2 — x ln x = 0Отрезок, содержащий корень: [1;2]Точное значение: 1,1183
	Печать фамилии, имени и отчества	Максимальный элемент в списке параметров	Добавление элемента с заданным номером в динамический массив	Метод половинного деления0,1×2 — x ln x = 0Отрезок, содержащий корень: [1;2]Точное значение: 1,1183
	Печать фамилии, имени и возраста	Количество четных элементов в списке параметров	Добавление элемента после элемента с заданным номером в динамический массив	Метод итераций3x — 4lnx — 5 = 0Отрезок, содержащий корень: [2;4]Точное значение: 3,2300
	Печать фамилии, курса и группы	Среднее арифметическое элементов в списке параметров	Номер максимального элемента в массиве	Метод Ньютона3x — 4lnx — 5 = 0Отрезок, содержащий корень: [2;4]Точное значение: 3,2300
	Печать фамилии, имени и рейтинга	Максимальный из элементов в списке параметров, стоящих на четных местах	Среднее арифметическое массива	Метод половинного деления3x — 4lnx — 5 = 0Отрезок, содержащий корень: [2;4]Точное значение: 3,2300
	Печать фамилии, курса и рейтинга	Максимальный из элементов в списке параметров, стоящих на нечетных местах	Количество отрицательных элементов в массиве	Метод итерацийОтрезок, содержащий корень: [0;1]Точное значение: 0,5629
	Печать фамилии, адреса и возраста	Минимальный из элементов в списке параметров, стоящих на четных местах	Добавление элемента с заданным номером в динамический массив	Метод НьютонаОтрезок, содержащий корень: [0;1]Точное значение: 0,5629
	Печать названия экзамена, количества сдающих и среднего балла	Минимальный из элементов в списке параметров, стоящих на нечетных местах	Сортировка массива методом простого обмена	Метод половинного деленияОтрезок, содержащий корень: [0;1]Точное значение: 0,5629
	Печать названия экзамена, даты экзамена и среднего балла	Среднее арифметическое из элементов в списке параметров, стоящих на четных местах	Минимальный элемент в массиве	Метод итераций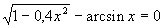Отрезок, содержащий корень: [0;1]Точное значение: 0,7672
	Печать координат точки	Среднее арифметическое из элементов в списке параметров, стоящих на нечетных местах	Сортировка массива методом простого выбора	Метод Ньютона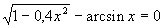Отрезок, содержащий корень: [0;1]Точное значение: 0,7672
	Вычисление и печать расстояния от точки с координатами x1,y1 до центра координат	Минимальный элемент в списке параметров	Сортировка массива методом простого включения	Метод половинного деления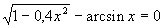Отрезок, содержащий корень: [0;1]Точное значение: 0,7672
	Вычисление и печать расстояния от точки с координатами x1,y1 до точки с координатами x2,y2	Максимальный элемент в списке параметров	Поиск заданного элемента в массиве	Метод итерацийex — e-x -2 = 0Отрезок, содержащий корень: [0;1]Точное значение: 0,8814
	Печать фамилии, имени и отчества	Количество четных элементов в списке параметров	Поиск заданного элемента в отсортированном массиве	Метод НьютонаМетод итерацийex — e-x -2 = 0Отрезок, содержащий корень: [0;1]Точное значение: 0,8814
	Печать фамилии, имени и возраста	Среднее арифметическое элементов в списке параметров	Удаление элемента с заданным номером из динамического массива	Метод половинного деленияМетод итерацийex — e-x -2 = 0Отрезок, содержащий корень: [0;1]Точное значение: 0,8814
	Печать фамилии, курса и группы	Максимальный из элементов в списке параметров, стоящих на четных местах	Удаление элемента с заданным ключом из динамического массива	Метод итераций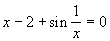Отрезок, содержащий корень: [1;2]Точное значение: 1,3077

Методические указания

1. В функции с умалчиваемыми параметрами использовать структурированный тип данных.

2. При демонстрации вызова функции с умалчиваемыми параметрами учесть, что опускать параметры функции можно только с конца.

3. В функции с переменными числом параметров можно использовать любой механизм определения конца списка параметров (передачу количества параметров как параметр функции или использование признака конца списка параметров).

4. Перегрузить функции для массивов типа char, int, и double.

5. Инстанцировать шаблон функции для типов char, int, и double.

6. Для нахождения корня уравнения написать как минимум две функции. Одна функция реализует уравнение, для которого вычисляется корень, другая — метод решения уравнения, указанный в варианте. Первая функция передается во вторую как параметр, с помощью указателя.

7. Точность нахождения корня уравнения выбирается не менее 0.001.

8. Полученный результат вычисления корня сравнить с точным значением, заданным в задании.

Содержание отчета

1. Постановка задачи (общая и для конкретного варианта).

2. Определения функций для реализации поставленных задач.

3. Определение функции main().

4. Тесты

Лабораторная работа №8

Статьи к прочтению:

Численные методы решения уравнений с одной переменной

Похожие статьи: