Dim org(50) as sotr, a as sotr

org(1).fam=Петров: org(1).zar=900: a.fam=Петров: a.zar=900

PRINT org(1).fam, org(1).zar

PRINT a.fam; a.zar

Именно переменная пользовательского типа должна быть указана в операторах PUT и GET.

Пример. Рассмотрим технику работы с файлом прямого доступа. Положим, следует повысить зарплату сотрудникам организации, получающим менее 850 руб. на определенный, задаваемый в момент просмотра данных, процент. Программа состоит из трех разделов. В первом – из массива S в файл KADR.DAT заносятся исходные данные. Во втором – просматриваются данные обо всех сотрудниках, получающих меньше 850. Каждому их них руководитель подразделения назначает (или не назначает) процент увеличения зарплаты. Если процент указан, предъявляется новая зарплата и, при нажатии любой клавиши, обработка данных продолжается. В третьем разделе программы на экран выводятся обновленные данные из файла.

Иванов N отдела: 123 Зарплата: 800

Укажите % повышение зарплаты =20 Будет – 960

Для продолжения нажмите любую клавишу

Программа работы с файлом прямого доступа

TYPE kadr’определение пользовательского типа данных

fam AS STRING * 12’фамилия

ot AS INTEGER’N отдела

zar AS LONG ‘зарплата

END TYPE

n=6’число сотрудников

DIM s(n) AS kadr’объявление массива записей для ввода

DIM w AS kadr’комбинированная переменная для вывода

DATA Иванов,123, 800, Петров, 564, 780, Сидоров, 123,950

DATA Ильин, 123, 700, Семина, 564, 600, Коваль, 123,900

READ s(1).fam, s(1).ot, s(1).zar, s(2).fam, s(2).ot, s(2).zar

READ s(3).fam, s(3).ot, s(3).zar, s(4).fam, s(4).ot, s(4).zar

READ s(5).fam, s(5).ot, s(5).zar, s(6).fam, s(6).ot, s(6).zar

OPEN kadr.dat FOR RANDOM AS 1’открытие файла KADR.DAT

FOR i=1 TO n’просмотр и запись данных в файл из массива S

PRINT s(i).fam, s(i).ot, s(i).zar

PUT #1, i, s(i)

FOR i = 1 TO n’анализ данных в файле

GET #1,i,w’чтение данных из файла в переменную W

IF w.zar

CLS

LOCATE 6, 20′

‘выводятся данные о сотруднике

PRINT w.fam;” N отдела:”; w.ot;” Зарплата:”; w.zar

LOCATE 8, 20′

‘определяется процент увеличения зарплаты

INPUT Укажите % повышение зарплаты =, x’

IF x0 THEN’если процент задан

w.zar=INT(w.zar*(1+x/100)) ‘вычисляется новая зарплата

LOCATE 8, 55′

PRINT Будет -; w.zar’вывод новой зарплаты

LOCATE 12, 23′

PRINT Для продолжения нажмите любую клавишу

SLEEP’ ‘пауза для просмотра

PUT #1, i, w’запоминание нового значения

END IF

CLS ‘просмотр новых данных

PRINT Новые данные

FOR i=1 TO n’

GET #1,i,w: PRINT w.fam, w.ot, w.zar’

@ Задачи для самостоятельного решения. Программа должна выполнять действия по обслуживанию файла (ввод, редактирование, удаление записей), а также по анализу содержащихся данных, возможно с вводом некоторых параметров с терминала.

1. uСоздать файл, содержащий сведения о количестве изделий, собранных рабочими завода за неделю. Каждая запись содержит поля: фамилия сборщика, количество изделий, собранных им ежедневно в течение пяти дней недели, т.е. в понедельник, вторник и т.д.

uНаписать программу, выдающую информацию: фамилию сборщика и общее число деталей, собранных им за неделю; фамилию сборщика, собравшего наибольшее число изделий и день, когда это произошло.

2. uСоздать файл, содержащий сведения о телефонных абонентах. Каждая запись имеет поля: фамилия абонента, номер телефона, год установки.

uНаписать программу, выдающую:

– по вводимой фамилии абонента сообщается номер его телефона;

– определяется количество установленных телефонов с любого, вводимого с терминала, года.

3. uСоздать файл, содержащий сведения о сдаче студентами сессии. Структура записи: номер группы, фамилия студента, оценки по четырем экзаменам и трем зачетам в форме з (зачет) и н (незачет).

uНаписать программу, выдающую:

– фамилии неуспевающих студентов с указанием номера группы и числа задолженностей;

– средний балл каждого студента и группы в целом.

РЕШЕНИЕ ЧИСЛЕННЫХ

ЗАДАЧ В EXCEL

Электронная таблица Excel располагает средствами, позволяющими решать средствами некоторые задачи вычислительной математики, не прибегая к программированию.

РЕШЕНИЕ УРАВНЕНИЙ

3.1.1. Решение нелинейных уравнений.Положим, нужно найти корень квадратного уравнения вида 0,5X2–3X+4=0. Решение будем искать в клетке А1, куда занесем исходное значение корня, например 0. Само уравнение внесем в А2. На рис.3.1.1а изображены эти клетки в числовой форме, на рис.3.1б – в виде формул. На рис.3.1в – результат вычислений, полученный с помощью инструмента Подбора параметра.

	A		A	A
				1,999964
			=0,5A1^2-3A1+4	3,56Е-05
Рис. 3.1.1а	Рис. 3.1.1б	Рис. 3.1.1в

Исходные значения параметров, участвующих в вычислениях, изображены на рис.3.1.1г в окне Подбор параметра. Точный корень нашего уравнения, как мы знаем, равен 2. Полученный результат очень близок, но не равен 2. Это естественно, поскольку Excel использует не аналитические (как мы привыкли), а численные, итерационные методы, заключающиеся в постепенном приближении получаемого решения к точному.

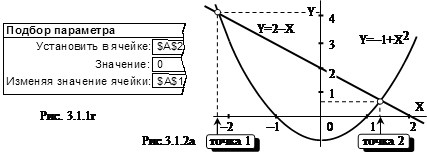
Критерием сходимости процесса считается близость очередного и предшествующего значений подбираемых решений. По умолчанию Excel выполняет до 1000 итераций или продолжает вычисления до достижения погрешности, не превышающей 0,0001. Если вы хотите изменить эти значения, следует в меню Сервис+Параметры во вкладке Вычисления осуществить необходимые установки. Нами получено одно из решений квадратного уравнения. Другое вещественное решение (если есть) возможно будет найдено, если задать иное начальное значение Х.

A	B	C
Начальноезначение	Формулы	Целеваяячейка
	=-1+A2^2	=СРОТКЛ(B2;B3)
	=2-A2	Рис.3.1.2б

3.1.2. Решение систем нелинейных уравнений.Положим, имеется система двух нелинейных уравнений:

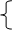Y= 2 – X

Y= –1+X2,

которые надо решить, т.е. найти точки их пересечения. Как видно на рис.3.1.2а, система имеет две такие точки.

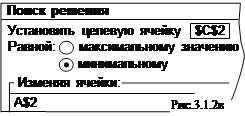Для решения системы построим таблицу (рис.3.1.2б), где в клетки В2 и В3 введем обе функции, которые в качестве аргумента Х ссылаются на ячейку А2. Кроме того, для контроля вычислений в С2 вводится целевая функция, которая вычисляет среднее отклонение значений функций друг от друга. Очевидно, если эти функции пересекаются (т.е. имеются решения), С2=0. Для розыска корня в окно Поиск решения вводятся необходимые параметры процесса (рис. 3.1.2в). Результат вычислений существенно зависит от начального значения, заданного в качестве решения. На рис.3.1.2г приведены исходный и конечный вид таблицы, если задать его равным +10 (решение Х=1,30278), а на рис. 3.1.2д, если -10 (решение Х=-2,303).

A	B	C		A	B	C
Начальноезначение	Формулы	Целеваяячейка		Начальноезначение	Формулы	Целеваяячейка
		53,5		1,30278	0,69722	2E-10
	-8				0,69722
		Рис.3.2	г
A	B	C		A	B	C
Начальноезначение	Формулы	Целеваяячейка		Начальноезначение	Формулы	Целеваяячейка
-10		43,5		-2,303	4,303	1E-08
					4,303
		Рис.3.2	д

Таким образом, в обоих случаях найдены два разных решения.

3.1.3. Решение систем линейных уравнений.Положим, нужно найти решение (корни) следующей системы линейных алгебраических уравнений:

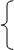2X1–1X2 + 1X3=3

1X1+3X2– 2X3=1

0X1+1X2 + 2X3=8

Внесем коэффициенты системы в таблицу на рис.3.1.3а. Свободные члены внесем в столбец Е. В столбец D внесем формулы вычисления свободных членов (D2=СУММПРОИЗВ($A$6:$C$6;A2:C2)). Наша задача – добиться совпадения значений вычисленных и фактических значений столбцов D и Е. В качестве изменяемых значений используются ячейки А6, В6, С6. Первоначально они остаются пустыми, т.е. равными нулю.

A	B	C	D	E
Х1	Х2	X3	Леваячасть	Свободныечлены
	-1
		-2

Корни:
1,00	2,00	3,00		Рис.3.1.3а

В окне Поиск решения вводятся значения только параметров: Изменяемые ячейки и Ограничения (рис.3.1.3б). Видим, что получены три корня: Х1=1, Х2=2, Х3=3.

Тест. 3.1.1. Что такое корень уравнения? 1). точка пересечения кривой с осью Х, 2). точка пересечения кривой с осью Y.

Тест. 3.1.2. Что такое линейное уравнение? 1). уравнение не содержащее произведений переменных, 2). уравнение не содержащее переменных в знаменателе, 3) уравнение не содержащее ни того и другого.

Статьи к прочтению:

EXPOSING Nithyananda : Nakkeeran Gopal Reveals the Story Part 03 |MT 66

Похожие статьи: