Движение тела с переменной массой: взлет ракеты

      Комментарии к записи Движение тела с переменной массой: взлет ракеты отключены

Рассмотрим указанную задачу в максимально упрощенной постановке. Наши цели:

а) достичь качественного понимания того, как скорость ракеты меняется во время взлета, как влияют на полет разные факторы;

б) оценить оптимальное соотношение параметров, при котором ракета достигнет первой космической скорости и сможет вывести на орбиту полезный груз.

Таким образом, обсуждаемая модель имеет черты как дескриптивной, так и оптимизационной.

Взлет ракеты — сложный процесс, который неизбежно следует огрубить в попытке получения относительно простых и качественно верных результатов. Например, примем, что сила тяги двигателя — величина постоянная на всем этапе разгона. Реально это, скорее всего, не так. но при упрощенном анализе колебаниями силы тяги пренебрежем, равно как и влиянием случайных порывов ветра и множеством других случайных и неслучайных факторов. Но при таком, даже самом упрощенном, анализе нельзя пренебречь наличием сопротивления воздуха, которое при высоких скоростях очень велико. Ни в коем случае нельзя пренебречь и убыванием массы ракеты в процессе взлета — оно огромно и составляет большую часть исходной массы. Так, у одной из крупнейших отечественных ракет «Энергия» стартовая масса составляет 20000 тонн, а к концу взлета всего 200 тонн.

Поиск математического описания проблем не составляет — в его основе все тот же второй закон Ньютона. Поскольку ракета очень быстро набирает столь высокую скорость, что линейной составляющей силы сопротивления заведомо можно пренебречь, то Fconp = k2v2. Примем, что топливо расходуется равномерно вплоть до его полного выгорания, т.е.

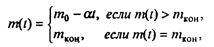
где m0 — начальная масса ракеты, ткон — конечная (т.е. масса полезного груза, выводимого на орбиту), ? — расход топлива; это допущение согласуется с допущением о постоянной силе тяги. Уравнение движения принимает вид в проекции на вертикальную ось

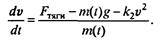(7.17)

Казалось бы, можно задаться некоторыми значениями величин Fтяги, т0, ?, k2 и проводить моделирование, но это была бы чисто формальная деятельность, не учитывающая еще одного важнейшего обстоятельства. Поскольку ракета взлетает на огромную высоту (сотни километров), ясно, что сила сопротивления в менее плотных слоях атмосферы не может быть такой же, как вблизи поверхности Земли (при равных скоростях). Действительно, в коэффициент k2 входит величина r -плотность окружающей среды, которая на «космических» высотах во много раз меньше, чем вблизи поверхности. Заглянем в справочник: на высоте 5,5 км плотность воздуха вдвое меньше, чем у поверхности, на высоте 11км- вчетверо и т.д. Математически зависимость плотности атмосферы от высоты хорошо передается формулой

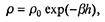
где b = 1,29•10-4 (h измеряется в метрах, ?0 — плотность вблизи поверхности Земли). Поскольку величина h меняется в ходе полета, уравнение для изменения h(t) следует добавить к уравнению (7.17) и записать следующую систему дифференциальных уравнений:

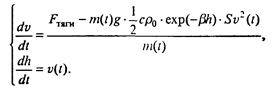(7.18)

Наша модель становится все более реалистической. Ее совершенствование можно продолжить — например, учесть наличие у ракеты нескольких ступеней, каждая из которых имеет свой запас топлива и тягу двигателя — считая, что после уменьшения массы до некоторого значения сила тяги скачком изменяется; оставим это для самостоятельных размышлений. Перед решением уравнений удобно обезразмерить переменные. Естественной характерной скоростью в данной задаче является первая космическая скорость v* ? 7,8 км/с, при которой возможен вывод на орбиту полезного груза; характерное время — момент полной выработки горючего

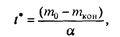
где mкон — масса груза. Реально t* — две-три минуты. За характерную высоту можно взять, например, h* — ту, на которой плотность атмосферы уменьшается в 10 раз (примерно 17 км). Последняя величина может показаться несколько произвольной (впрочем, она таковой и является), но все равно удобнее измерять расстояния в данной задаче относительно величины, равной нескольким километрам, чем в метрах в системе СИ. Итак, введя безразмерные переменные

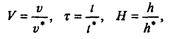
после несложных преобразований получим уравнения

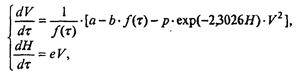(7.19)

где f(?) — известная функция:

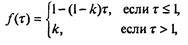
а безразмерные параметры a, b, p, e, k выражаются через исходные так:

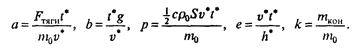
То, что f(?) определяется двумя формулами, связано с наличием двух этапов полета: до и после выработки топлива. Безразмерное время, разделяющее эти этапы — ? = 1; если к этому моменту безразмерная скорость V ? 1, то первая космическая скорость достигнута, в противном случае — нет. Параметр а управляет режимом полета; если при достижении величиной V значения, равного единице, топливо еще не все выработано (т.е. ?1), можно с этого момента либо положить а = 0 («выключить двигатель»), либо продолжать разгон — в зависимости от постановки задачи. Рис. 7.13 иллюстрирует влияние изменения параметра о на динамику взлета ракеты в рамках принятых выше предположений при фиксированных значениях остальных параметров.

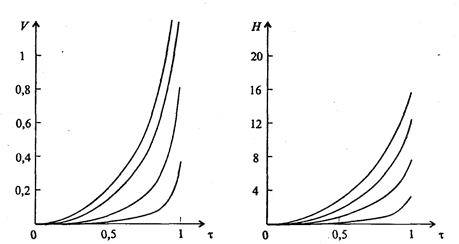
Рис. 7.13. Зависимости V(?) и H(?) при а = 0,2, a = 0,3, a = 0,4 и а = 0,5

(кривые на рисунках слева направо)

ДВИЖЕНИЕ НЕБЕСНЫХ ТЕЛ

Как движется Земля и другие планеты в пространстве? Что ждет комету, залетевшую из глубин космоса в Солнечную систему? Многовековая история поиска ответов на эти и другие вопросы о движении небесных тел хорошо известна; для многих людей, внесших большой вклад в науку, именно интерес к астрономии, устройству большого мира, был первым толчком к познанию.

По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Если поместить начало системы координат на одном из тел (размерами тел по сравнению с расстоянием между ними будем пренебрегать), математическая запись силы, действующей на второе тело, имеет вид (рис. 7.14)

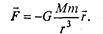(7.20)

Здесь G = 6,67•10-11 м3/кг•с2) — гравитационная постоянная.

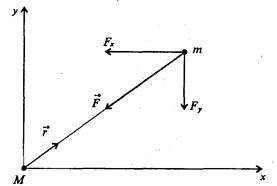
Рис. 7.14. Выбор системы координат при решении задачи двух тел

Знак «минус» в формуле (7.20) связан с тем, что гравитационная сила является силой притяжения, т.е. стремится уменьшить расстояние г между телами.

Далее мы ограничимся лишь изучением взаимного движения двух тел. При этом возникает непростой вопрос: с какой позиции (в какой системе координат) изучать это движение? Если делать это из произвольного положения — например, наблюдатель с Земли изучает взаимное движение Солнца и планеты Юпитер — задача станет для нас слишком сложной. Ограничимся лишь простейшей ситуацией: рассмотрим движение одного из тел с точки зрения наблюдателя, находящегося на втором, т.е., например, движения планеты или кометы относительно Солнца, Луны относительно Земли, пренебрегая при этом относительно небольшими силами притяжения от всех прочих небесных тел. Разумеется, мы тем самым произвели ранжирование факторов, и наши последующие действия имеют отношение к реальности лишь в меру соблюдения определенных условий.

Уравнение, описывающее движение тела m в указанной системе координат, имеет вид

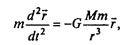
или в проекциях на оси х, у

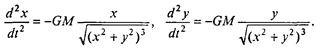(7.21)

Интересующая нас орбита сильно зависит от «начальной скорости» тела т и «начального расстояния». Мы взяли эти слова в кавычки, так как при изучении движения космических тел нет столь отчетливо выделенного «начального момента», как в ранее рассмотренных ситуациях. При моделировании нам придется принять некоторое положение условно за начало, а затем изучать движение дальше. Очень часто космические тела движутся практически с постоянной скоростью по орбитам, близким к круговым. Для таких орбит легко найти элементарное соотношение между скоростью и радиусом. В этом случае сила тяготения выступает в роли центростремительной, а центростремительная сила при постоянной скорости выражается известной из начального курса физики формулой mv2/r. Таким образом, имеем

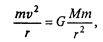
или

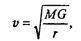(7.22)

— искомое соотношение.

Период движения по такой орбите

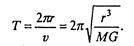
Заметим, что отсюда вытекает один из законов Кеплера, приведший Ньютона к открытию закона всемирного тяготения: отношение кубов радиусов орбит любых двух планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца, т.е. 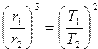. Более точная формулировка дана ниже (так как реально орбиты планет не вполне круговые). Если соотношение (7.22) нарушено, то орбита не будет круговой. Выяснить, какой она будет, можно в ходе численного моделирования. Сведем (7.21) к системе четырех дифференциальных уравнений первого порядка:

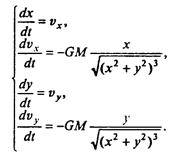(7.23)

В этой задаче особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ? = 1,496•1011 м, (так называемая, астрономическая единица), период круговой орбиты 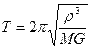,соответствующий этому расстоянию, скорость движения по ней 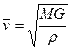, т.е. принять

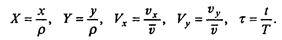
После обезразмеривания получаем

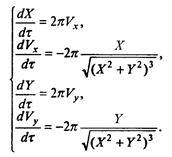(7.24)

Отметим замечательное обстоятельство: в безразмерных переменных уравнения вообще не содержат параметров! Единственное, что отличает разные режимы движения друг от друга — начальные условия.

Можно доказать, что возможные траектории движения, описываемые уравнениями (7.24) — эллипс, парабола и гипербола.

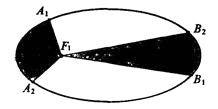
Рис. 7.15. Иллюстрация второго закона Кеплера

Напомним законы Кеплера, рис. 7.15.

1. Всякая планета движется по эллиптической орбите с общим фокусом, в котором находится Солнце.

2. Каждая планета движется так, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади; на рисунке промежутки времени движения от A1 к A2 и от B1 к B2 считаются одинаковыми, а площади секторов F1A1А2 и F1B1B2 равны. Это означает, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите.

3. Отношение кубов больших полуосей орбит двух любых планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца.

Уравнения (7.24) описывают движение не только планет, но и любых тел, попадающих в поле тяготения большой масcы. Так, в Солнечной системе существует огромное количество комет, движущихся по чрезвычайно вытянутым эллиптическим орбитам с периодами от нескольких земных лет до нескольких миллионов земных лет. Судьбы небесных тел, не являющихся постоянными членами Солнечной системы, а залетевших в нее издалека, определяютсяих скоростью-еслионадостаточно велика, то орбита будет гиперболической, и. облетев Солнце, тело покинет Солнечную систему, если нет — перейдет на эллиптическую орбиту и станет частью системы; пограничная между ними орбита — параболическая.

Все эти утверждения можно проверить и детально исследовать с помощью уравнений (7.24). При этом полезно и удобно использовать одно важнейшее свойство обсуждаемой системы, которого не было у рассмотренных ранее — сохранение полной энергии движущегося тела (такое свойство называется «консервативность»). Полная энергия движущегося небесного тела т в системе двух тел имеет значение

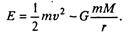
Первое слагаемое — кинетическая, второе — потенциальная энергия. В безразмерных переменных

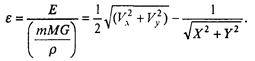
Наличие неизменного параметра е в ситуации, когда изменяются Vx, Vy, X, Y, позволяет контролировать процесс решения системы дифференциальных уравнений, проверять устойчивость метода, подбирать шаг интегрирования.

Статьи к прочтению:

Реактивное движение. Ф-ла Мещерского


Похожие статьи: