Метод наименьших квадратов (мнк)

Автор: ·

Аппроксимация на основе интерполяции не имеет смысла или невозможна, когда исходные данные содержат погрешности, повторы или очень большое количество точек. В этих случаях используют сглаживание: критерий близости аппроксимирующей функции 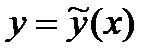к исходным данным 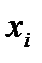, 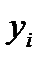рассматривается как минимальное отклонение значений в заданных точках. Количественно отклонение может быть оценено методом наименьших квадратов (МНК), согласно которому необходимо минимизировать сумму квадратов: где 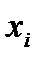,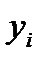— значения данных 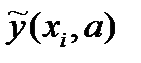— значение аппроксимирующей функции в точке ; 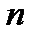— число данных, 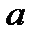— незвестные параметры. Задача сводится к нахождению экстремума функции параметров 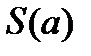. Линейная аппроксимация. В случае линейной формулы 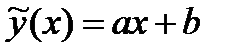сумма квадратов принимает вид: 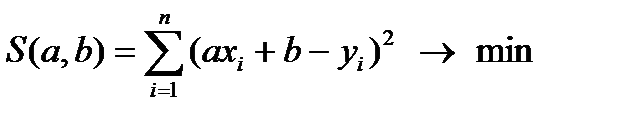. Эта функция имеет минимум в точках, в которых частные производные от 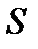по параметрам 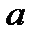и 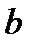обращаются в нуль, т.е. ,

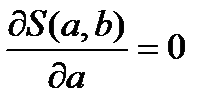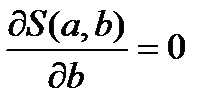
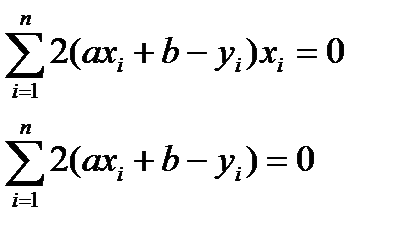
Решая систему уравнений, получим значения 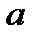и 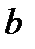уравнения .

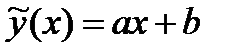Полиномиальная аппроксимация. В случае выбора зависимости в виде полинома, например, 2-й степени 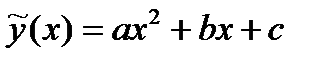сумма квадратов принимает вид: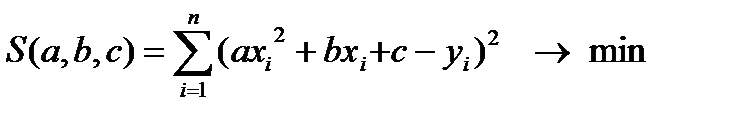

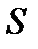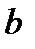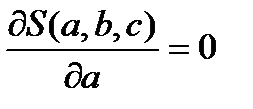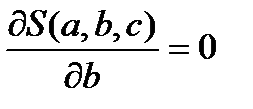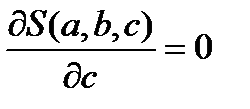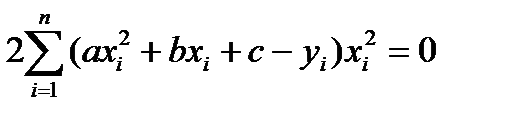
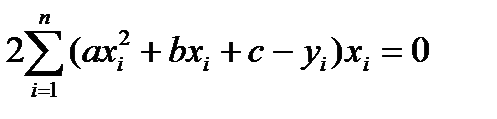
Эта функция имеет минимум в точках, в которых частные производные от по параметрам , , обращаются в нуль, т.е.: , , В результате дифференцирования и элементарных преобразований для определения параметров получают систему из трех линейных уравнений с тремя неизвестным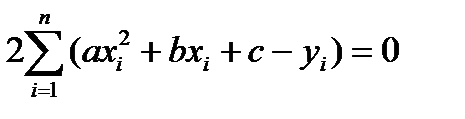и: Или

При расчете удобно использовать таблицу

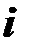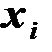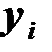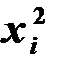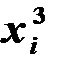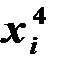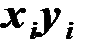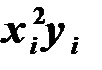-2 -8 -12

Точность аппроксимацииможно оценить среднеквадратической ошибкой

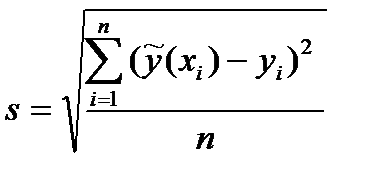, которая не должна превышать погрешность исходных данных.

Формулы численного интегрирования Формулы прямоугольников и трапеций.

Численное интегрирование.

Требуется вычислить определенный интеграл: 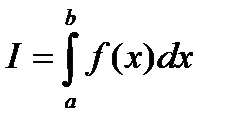. Выберем на отрезке интегрирования 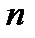различных узлов 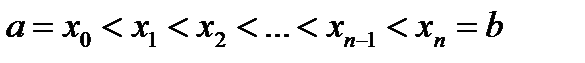и интерполируем функцию 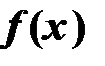по ее значениям в этих узлах некоторым полиномом 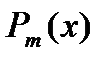. Тогда определенный интеграл приближенно можно вычислять по формуле ,

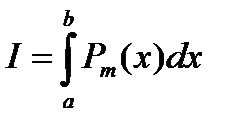Метод прямоугольников.

На каждом отрезке 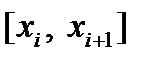, 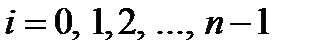функция 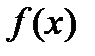заменяется полиномом нулевой степени 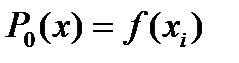. Поэтому приближенно I вычисляется по формуле:

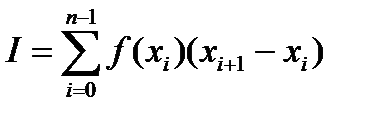Для равноотстоящих узлов формула имеет следующий вид:

— формула левыхпрямоугольников.

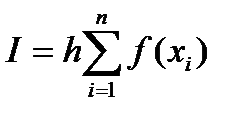— формула правых прямоугольников.

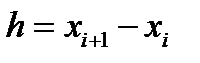
Программа вычисления интеграла методом прямоугольников. Исходные данные: пределы интегрирования и число разбиений.

Function f(x). f = Sqr(2 * x ^ 2 + 1). 0End Function. Sub Integral()

a = Cells(1, 2). b = Cells(2, 2). n = Cells(3, 2). h = (b — a) / n. x = a. S = 0

1 s = s + f(x) * h. x = x + h. If xb Then GoTo 1. Cells(5, 2) = s.End Sub

Метод трапеций.

В этом методе на каждом отрезке функция f(x) заменяется полиномом 1-й степени .

По формуле Лагранжа:

. Интегрируя на отрезке , получим:

. Суммируя по всем( ), получим формулу трапеций:

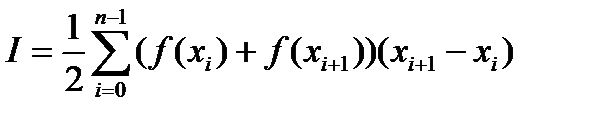. Для равноотстоящих узлов , , …,

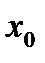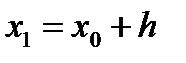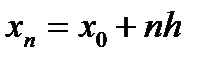
формула принимает следующий вид: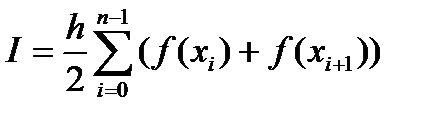

Программа вычисления интеграла методом трапеций:

в программе, заменить отмеченные строки на следующие:

1 s = s + 0.5 * (f(x) + f(x + h)) * h

x = x + h

Статьи к прочтению:

Квадрат — Русский трейлер (2017)


Похожие статьи:

Метки:

Читайте также:

Последняя инфа: