Методические указания по организации самостоятельной работы студентов

Одними из базовых арифметических операций в компьютерной системе являются арифметические операции сложения и вычитания, при выполнении которых используются поразрядные логические операции, а также операции сдвигов.

Компьютерная система выполняет сложение и вычитание операндов по правилам сложения и вычитания двоичных чисел рис.2.1.

Правиласложения:	Правилавычитания:
1. 0 + 0 = 0	1. 0 — 0 = 0
2. 0 + 1 = 1	2. 1 — 1 = 0
3. 1 + 0 = 1	3. 1 — 0 = 1
4. 1 + 1 = 10	4. 10 — 1 = 1

Рисунок 2.1 — Правила сложения и вычитания двоичных чисел

При сложении беззнаковых операндов, находящихся в регистрах процессора, алгоритм выполнения операции отслеживается по счетчику тактов, начиная с младшего бита, и количество тактов равно разрядности регистра процессора. Для выполнения алгоритма сложения двоичных беззнаковых чисел в компьютерных системах можно ввести следующие обозначения: 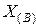— значение слагаемого в регистре 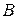; 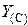— значение слагаемого в регистре 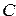; 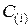— перенос в следующий разряд; 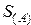— сумма в регистре 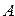. 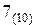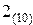Например, необходимо перевести в двоичную систему счисления, а затем сложить два числа ( ) и ( ), записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел). Длина разрядной сетки операндов равна пяти битам. Используя вышеописанные правила, мы находим сумму двоичных чисел как показано на рис. 2.2 и в таблице 2.1. Проблем не возникает до тех пор, пока значение результата не превышает разрядной сетки операнда.

;

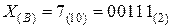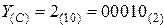regB

regC

Рисунок 2.2 — Исходные данные для выполнения операции сложения двух двоичных беззнаковых чисел

Таблица 2.1 — Алгоритм сложения двух двоичных беззнаковых чисел

Такты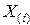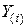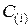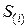

В результате сложения двух двоичных беззнаковых чисел получена сумма, представленная на рис.2.3.

regA

Рисунок 2.3 — Результат выполнения алгоритма сложения двух двоичных беззнаковых чисел

При выполнении арифметических операций непосредственное участие в алгоритме сложения и вычитания принимает операционный автомат ( 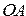) (рис.2.4). На рис.2.4 приняты следующие сокращения:

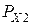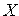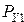— регистр для хранения операнда ;

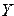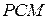— регистр для хранения суммы;

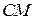— одноразрядный сумматор;

— флаг (триггер) переноса;

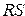— сигнал сдвига влево регистра на один разряд;

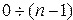— разрядность регистра (процессора).

На этой функциональной схеме прямоугольниками обозначены регистры (устройства для хранения информации), трапецией — комбинационные схемы (устройства для преобразования информации без ее запоминания). В состав ( ) входят регистры, триггеры, комбинационные схемы, связанные между собой и таким образом, чтобы можно было выполнить определенный алгоритм (алгоритмы). Операционный аппарат представляет собой простой цифровой процессор. С помощью специальных управляющих сигналов, процессор определяет, какую именно арифметическую операцию — сложения, вычитания, умножения или деления — он будет выполнять. Структура операционного аппарата для выполнения арифметических операций двоичных беззнаковых чисел приведена на рис.2.4.

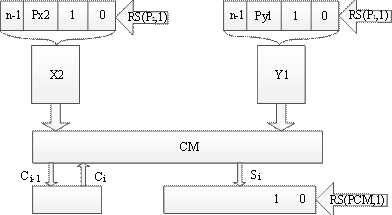
Рисунок 2.4 — Функциональная схема ( ) для операции сложения двоичных беззнаковых чисел

Для того, чтобы компьютерная система могла оперировать как положительными, так и отрицательными числами, в разрядную сетку компьютерного представления числа вводится знаковая часть. Разработчики компьютерных систем самый крайний левый бит отвели под знак и приняли следующее обозначение: если самый крайний левый бит в разрядной сетке представления числа содержит ( ) — это означает положительное двоичное число; если самый крайний левый бит в разрядной сетке представления числа содержит ( ) — это означает отрицательное двоичное число. На рис.2.5 представлен формат числа в двоичной системе счисления со знаковым битом.

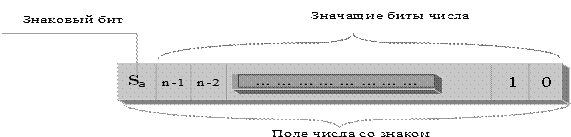
Рисунок 2.5 — Формат числа в двоичной системе счисления со знаковым битом

Исходя из вышесказанного будем обозначать целые знаковые числа в виде:

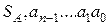, (2.1)

где 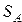— знаковый бит числа ( );

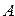— цифры слева от запятой.

Неправильные дроби:

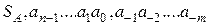, (2.2)

где 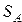— знаковый бит числа ( );

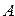— цифры слева от запятой;

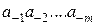— цифры справа от запятой.

А правильные дроби:

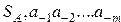, (2.3)

где 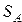— знаковый бит числа ( );

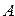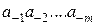— цифры справа от запятой.

В связи с тем, что алгоритмы выполнения операций в компьютерных системах имеют свою специфику, возникает проблема представления отрицательных чисел.

Ее решают за счет использования особых способов кодирования числовых данных.

Рассмотрим три наиболее распространенных кода, которые применяются на практике: прямой код, обратный код, дополнительный код.

Прямой код. Наиболее естественный код.

Формируется следующим образом: в знаковый бит ( 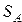) числа помещают знак числа ( — если число положительное и — если число отрицательное ), а остальные биты используют для абсолютного значения (модуля) числа.

Правило преобразования чисел в прямом коде можно записать следующим образом:

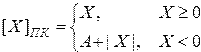, (2.4)

где 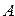— вес старшего разряда в 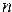— разрядной сетке, .

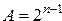Отображение числовой оси двоичных чисел на числовую ось 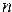— битных наборов (прямой код ) для компьютерной системы показано на рис. 2.6.

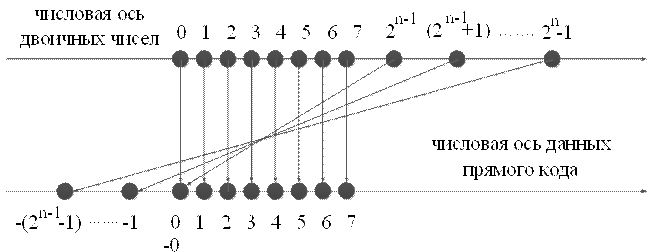
Рисунок 2.6 — Отображение числовой оси двоичных чисел на числовую ось 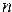— битных наборов (прямой код )

В табл.2.2. представленны данные с помощью которых построены числовые оси на рис.2.6.

Таблица 2.2 — Данные с помощью которых построены числовые оси на рис.2.6.

А(10)	А(2)	А(ПК)	Знаки
		0,111	+7
		0,110	+6
		0,101	+5
		0,100	+4
		0,011	+3
		0,010	+2
		0,001	+1
		0,000	+0
8		1,000	-0
		1,001	-1
		1,010	-2
		1,011	-3
		1,100	-4
		1,101	-5
		1,110	-6
		1,111	-7

Диапазон представимых чисел: 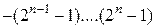. Положительный момент заключается в удобстве операции ввода-вывода данных.

Отрицательный момент в том, что существует два представления ( ) и операция алгебраического сложения требует анализа знаков и модулей операндов, и выбора фактической операции сложения или вычитания.

Обратный код.Обратный 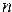— разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака ( ), за которым следует ( 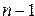) разрядное двоичное представление модуля числа, то есть обратный код для положительного числа совпадает с прямым кодом.

Обратный 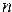— разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака ( ), за которым следует ( 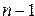) разрядное двоичное число, представляющее собой инвертированное ( 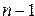) разрядное представление модуля числа, то есть для отрицательного числа все цифры числа заменяются на противоположные, а именно ( на , а на ) и в знаковый разряд заносится единица.

Обратный код числа определяется соотношением:

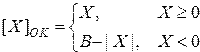, (2.5)

где 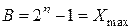— максимальное число в 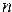— разрядной сетке.

Отображение числовой оси двоичных чисел на числовую ось 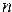— битных наборов (обратный код ) для компьютерной системы показано на рис. 2.7.

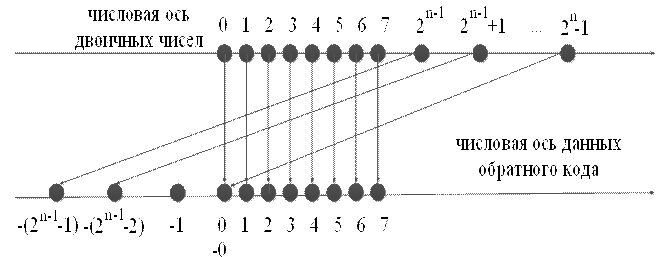
Рисунок 2.7 — Отображение числовой оси двоичных чисел на числовую ось 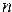— битных наборов (обратный код )

В табл.2.3 представленны данные с помощью которых построены числовые оси на рис. 2.7.

Таблица 2.3 — Данные с помощью которых построены числовые оси на рис.2.7.

А(10)	А(2)	А(ПК)	Знаки
		0,111	+7
		0,110	+6
		0,101	+5
		0,100	+4
		0,011	+3
		0,010	+2
		0,001	+1
		0,000	+0
15		1,111	-0
		1,110	-1
		1,101	-2
		1,100	-3
		1,011	-4
		1,010	-5
		1,001	-6
		1,000	-7

Диапазон представимых чисел: 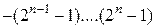. Положительный момент заключается в том, что при сложении обратных кодов чисел как беззнаковых чисел получаем обратный код суммы.

Отрицательный момент заключается в том, что существует два представления ( ) и при выполнении операций сложения в обратном коде требуется коррекция суммы с помощью циклического переноса единицы переполнения из знаковых разрядов суммы.

Дополнительный код. Наиболее распространенный способ представления отрицательных целых чисел в компьютерных системах.

Он позволяет заменить операцию вычитания на операцию сложения, чем упрощает архитектуру компьютерной системы.

Дополнительный код является дополнением числа до некоторого граничного числа 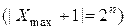. Дополнительный код положительного числа совпадает с прямым кодом.

Для получения дополнительного кода отрицательного числа существует три способа:

1) все цифры модуля исходного числа заменяются на взаимно обратные, то есть производится инверсия всех цифр числа, затем к полученному значению добавляется единица в младшем разряде;

2) из модуля числа вычитается ( ) младший бит, а затем инвертируются все разряды; 3) необходимо записать 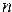— битный модуль числа.

Затем просматривать число справа налево, сохранить все младшие нули и первую встретившуюся ( ), а остальные биты инвертировать.

Дополнительный код числа определяется соотношением:

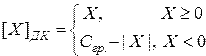, (2.6)

где 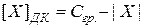равняется весу не существующего в данном числе разряда, расположенного слева от знаковой цифры.

Отображение числовой оси двоичных чисел на числовую ось 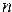— битных наборов (дополнительный код ) для компьютерной системы показано на рис. 2.8. Диапазон представимых чисел: .

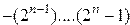Свойства дополнительного кода: при сложении чисел в дополнительном коде как беззнаковых чисел получаем дополнительный код суммы.

Знаковые биты суммируются обычным образом, а возникающий при их сложении перенос игнорируется; любое число в дополнительном коде можно считать младшими битами («хвостом») числа любой длины, если содержимое знакового бита копировать влево.

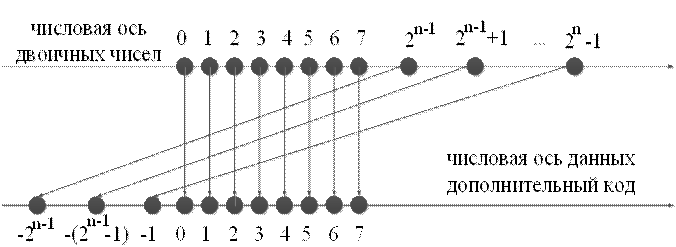
Рисунок 2.8 — Отображение числовой оси двоичных чисел на числовую ось 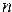— битных наборов (дополнительный код )

Эта операция называется расширением знака. Используется, когда исходные операнды в операциях сложения и вычитания имеют разную длину.

В табл.2.4 представленны данные с помощью которых построены числовые оси на рис.2.8.

Таблица 2.4 — Данные с помощью которых построены числовые оси на рис.2.8.

А(10)	А(2)	А(ПК)	Знаки
		0,111	+7
		0,110	+6
		0,101	+5
		0,100	+4
		0,011	+3
		0,010	+2
		0,001	+1
		0,000
		1,111	-1
		1,110	-2
		1,101	-3
		1,100	-4
		1,011	-5
		1,010	-6
		1,001	-7
		1,000	-8

Свойства кодов:

1. Операции должны выполняться над данными, представленными в одном и том же коде: , , ;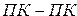

2. Положительные числа в 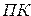, , 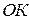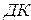не меняют своего представления;

3. Результат выполнения операций сложения и вычитания над числами, представленными в 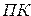, , 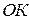или 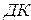, являются 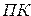, , 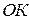или 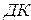соответственно;

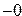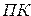4. Двоичный набор, представляющий ( ) в и 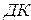, является запрещенной комбинацией;

5. В отличие от 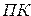, , 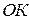в 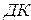нельзя отбрасывать нули после знакового разряда в целой части и нули в конце дробной части отрицательного числа (разрешается отбрасывать ).

Для корректного выполнения операций в компьютерной системе существует регистр флагов табл.2.5.

Таблица 2.5 — Регистр флагов — FLAGS

Бит

Флаг

IOPL

В регистре флагов, находится группа флагов, которые отвечают за корректность выполнения арифметических операций. Эти флаги, служат признаками, представляющими общую характеристику результата выполнения арифметических операций. Наиболее широко применяются следующие арифметические флажки:

— флажок переноса (Flag Carry), обозначаемый (FC). Устанавливается в (1) в двух случаях: 1)если при выполнении операции сложения имеет место перенос из старшего бита результата (представляет собой расширение результата на 1 бит влево); 2) если при выполнении операции вычитания имеет место заем (borrow) в старший бит. Это возможно в случае, если уменьшаемое меньше вычитаемого. Если операнды интерпретируются как беззнаковые числа, данный флажок является признаком переполнения компьютерной системы.В операциях над знаковыми числами самостоятельного значения не имеет.

— флажок вспомогательного переноса или дополнительный перенос (Flag Auxiliary), обозначаемый (FA). При сложении показывает перенос, а при вычитании — заем из младшей тетрады (бит 3) результата. Используется в операциях двоично-десятичной арифметики.

— флажок нуля (Flag Zero), обозначаемый (FZ). Признак нулевого результата. Устанавливается в (1) когда результат выполнения операции равняется (0).

— флажок знака (Flag Sign), обозначаемый (FS). Повторяет состояние знакового бита.

— флажок переполнения (Flag Overflow), обозначаемый (FО). В операциях над знаковыми числами показывает, находится ли результат внутри диапазона представимых чисел:

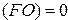— – результат правильный;

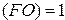— – возникло переполнение. Следует отметить, что (FO) устанавливается в (1), если перенос в старший разряд и из него не совпадают.

При выполнении операций сложения и вычитания чисел в дополнительных кодах обрабатывающее устройство компьютера не делает различий между знаковыми и беззнаковыми операндами.

То есть операнды должны интерпретироваться самим пользователем как знаковые или беззнаковые.

В операции вычитания используется дополнительный код вычитаемого.

Если длина операндов превышает длину машинного слова, то сложение и вычитание выполняют в несколько приемов, организуя программный цикл.

Операцию начинают с младших частей операндов, «продвигаясь» далее в сторону старших частей.

На каждом шаге должны обрабатываться возникающие переносы (или заемы), при этом могут возникнуть четыре случая.

Обозначения принятые на рис.2.9 — 2.11:

— над стрелкой обозначает — (нет);

— над стрелкой обозначает -(да);

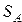— — знаковый бит;

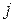— — старший значащий бит;

— — младший значащий бит.

Случай №1.При выполнении арифметической операции (рис.2.9) (а) возникла следующая ситуация:

1. Отсутствует переход из старшего значащего бита в знаковый.

2. Отсутствует переход из знакового бита за пределы разрядной сетки.

3. Флаг переполнения .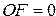

4. Флаг переноса .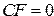

5. Флаг знака 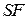повторяет значение знакового бита.

6. Флаг нуля , если результат выполнения арифметической операции получился равен нулю, то значение флага устанавливается равным единице, в противном случае — нулю.

Случай №2.При выполнении арифметической операции (рис.2.9) (б) возникла следующая ситуация:

1. Есть переход из старшего значащего бита в знаковый.

2. Есть переход из знакового бита за пределы разрядной сетки.

3. Флаг переполнения .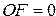

4. Флаг переноса .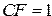

5. Флаг знака 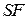повторяет значение знакового бита.

а)

б)

Рисунок 2.9 — Пример отсутствия переполнения разрядной сетки КС

Случай №3.При выполнении арифметической операции (рис.2.10) возникла следующая ситуация:

1. Есть переход из старшего значащего бита в знаковый.

2. Отсутствует переход из знакового бита за пределы разрядной сетки.

3. Флаг переполнения 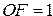, есть переполнение в области положительных чисел.

4. Флаг переноса .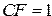

5. Флаг знака 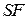повторяет значение знакового бита.

Случай №4.При выполнении арифметической операции рис.2.11 возникла следующая ситуация:

1. Отсутствует переход из старшего значащего бита в знаковый.

2. Есть переход из знакового бита за пределы разрядной сетки.

3. Флаг переполнения 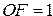, есть переполнение в области отрицательных чисел.

4. Флаг переноса .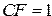

5. Флаг знака 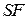повторяет значение знакового бита.

Рисунок 2.10 — Пример переполнения разрядной сетки КС в области положительных чисел

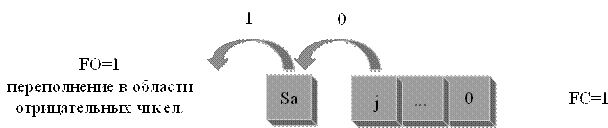Рисунок 2.11 — Пример переполнения разрядной сетки КС в области отрицательных чисел

При выполнении арифметических операции знакового сложения и вычитания могут возникнуть следующие случаи:

Случай №1.Известно, что 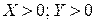, тогда:

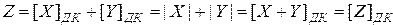Случай №2.Известно, что 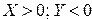и , тогда:

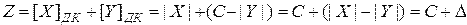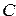( ) эквивалентно переносу в знаковый разряд, т.к.: .

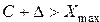Тогда: .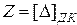

Случай №3.Известно, что 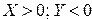и 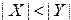, тогда: , по сути, представляет собой дополнительный код отрицательной разности:

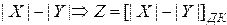, так как: .

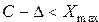Случай №4.Известно, что 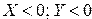, тогда:

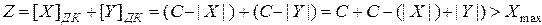Первое ( 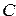) игнорируется, т.к. эквивалентно переносу в знаковый разряд, а 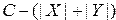— 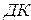суммы модулей. При условии, что .

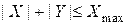Контрольные вопросы

1. Какие флаги в регистре флагов, отвечают за корректность выполнения арифметических операций сложения и вычитания.

2. Сформулируйте правила сложения и вычитания двоичных чисел.

3. Как представляются двоичные числа в прямом, обратном и дополнительном коде.

4. Назовите свойства прямого, обратного и дополнительного кодов.

5. Объясните принцип работы флага .

6. Объясните принцип работы флага .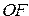

7. Объясните принцип работы флага .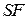

8. Объясните принцип работы флага .

9. Назовите случаи, которые могут возникнуть при выполнении арифметических операций знакового сложения и вычитания.

Методические указания по организации самостоятельной работы студентов

Статьи к прочтению:

Методический семинар И. А. Смирнова, победителя Всероссийского конкурса \

Похожие статьи: