Общие рекомендации по выполнению расчетно-графической работы

ВВЕДЕНИЕ

В число дисциплин, составляющих основу архитектурного образования, входит архитектурное черчение. Его изучение развивает пространственное представление, что необходимо всем специалистам, использующим в своей деятельности геометрические модели, а в особенности архитектору, который для фиксации композиционных замыслов пространственного объекта использует плоские изображения.

Предметом архитектурного черчения является изложение и обоснование способов построения изображений пространственных форм на плоскости. Изображения, построенные по правилам, изучаемым в архитектурном черчении, позволяют мысленно представить форму предметов и их взаимное расположение в пространстве.

Задача изучения архитектурного черчения сводится к изучению способов получения графических моделей пространства, основанных на ортогональном и центральном проецировании и умению решать задачи, связанные с пространственными формами и отношениями.

Изучение разделов «Точка, прямая, плоскость», «Взаимное положение плоскостей», «Пересечение поверхностей», «Тени в ортогональных проекциях», «Аксонометрия и тени в аксонометрии» необходимо для приобретения навыков и знаний, позволяющих составлять и читать архитектурно-строительные чертежи, а также для развития пространственного воображения.

Построение теней в архитектурной практике имеет важное значение. Для проверки композиционных решений и придания архитектурным чертежам большей наглядности, рельефности изображений проектировщик сопровождает их построением теней. Архитектурно-строительный чертеж с изображением светотени значительно полнее создает представление о реальном объекте. Даже по одной проекции, дополненной построением теней, можно «прочитать» чертеж, т.е. представить пространственное решение композиции, масштабность деталей и т.д.

Способом закрепления теоретического материала курса является умение решать разнообразные графические задачи, позволяющие определять положение геометрических объектов в пространстве, их размеры и взаимное расположение. Результатом приобретенных знаний и навыков являются, в конечном итоге, четкие пространственные представления, позволяющие не только понимать, но и создавать компьютерные изображения сложных объектов.

ОБЩИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Расчетно-графическая работа представляет собой альбом чертежей, выполненных по индивидуальному заданию и оформленных в соответствии с нижеизложенными требованиями.

Каждое задание выполняется на отдельном листе плотной чертежной бумаги формата А3 (297?420 мм). Поле чертежа ограничивается рамкой слева – 20 мм от линии обреза листа, с остальных сторон – 5 мм. В правом нижнем углу вплотную к рамке помещается основная надпись, выполненная по типу, приведенному на рисунке 1.

Все построения необходимо вести карандашом с соблюдением принятых условностей чертежа, с хорошим качеством оформления в части графики, обозначений и надписей.

На чертеже должны сохраняться вспомогательные линии построения и обозначения основных точек. Шрифт – по усмотрению студента, но аккуратно выполненный и четкий.

Если на чертеже строятся тени, то они покрываются слабым тоном туши или акварели, при этом падающие тени должны быть интенсивнее собственных. Штриховка в этих случаях не рекомендуется, как очень трудоемкая работа, не всегда дающая хороший результат.

Рисунок 1 – Пример заполнения основной надписи

При выполнении на чертеже нескольких изображений их расположение и общая компоновка должны быть заранее рассчитаны.

Листы выполненной расчетно-графической работы скрепляются в альбом. Образец титульного листа приведен в приложении А.

Обозначения геометрических элементов принимаются согласно таблице 1.

Таблица 1 – Обозначения основных геометрических элементов

Элементы	Обозначение
Плоскости проекций:горизонтальная……………………………………….фронтальная………………………………….профильная…………………………………..дополнительная………………………………	HVWS, T, …
Оси проекций основные	x, y, z, V/H, V/W
Оси при введении дополнительной плоскости проекций	H/S, V/T, …
Точки в пространстве	A, B, C и другие прописные буквы латинского алфавита, а также цифры
Линии в пространстве	По точкам, определяющим линию
Отрезки прямых	AB, CD, EF и в других сочетаниях прописных букв
Плоскости и поверхности	P, Q и другие прописные буквы латинского алфавита
Следы прямойгоризонтальный………………………………..фронтальный…………………………….	MN
Проекции точек:горизонтальная…………………………………фронтальная………………………………профильная………………………………….на дополнительной плоскости проекций…..	a, b, …а’, b’, …a», b», …a , b , a , …
Проекции линий	По проекциям точек, определяющим линию
Проекции отрезка прямой:горизонтальная…………………………………фронтальная……………………………..профильная…………………………………на дополнительной плоскости проекций….	ab, a1, …a’b’, a’1′ , …a»b», a»1», …a b , a b , …

СОДЕРЖАНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Задание 1. Точка. Прямая. Плоскость.

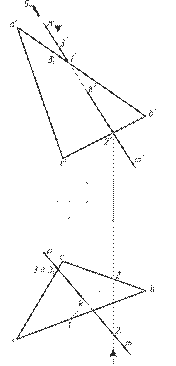
По заданным координатам точек построить треугольник ABC и прямую DE.

1. Через прямую DE провести плоскость, перпендикулярную плоскости АВС, построить линию их пересечения, определить видимость.

2. Построить следы плоскости АВС на плоскости проекций.

3. Построить плоскость, параллельную плоскости АВС и отстоящую от нее на 40 мм.

Индивидуальные варианты заданий приведены в таблице 2.

Таблица 2 – Варианты задания 1

Вариант

Координаты точек

Методические указания.Для выполнения графического задания необходимо проработать следующие теоретические вопросы: главные линии плоскости; перпендикулярность прямой и плоскости; пересечение прямой и плоскости; пересечение плоскостей; параллельность плоскостей; определение натуральной величины отрезка.

Задачи 1 и 2 совместить на одном чертеже и расположить в левой половине листа, задачу 3 – в правой. В верхнем левом углу листа вычертить таблицу с координатами точек. Работу начать с построения проекций точек, приняв 1 см за 10 единиц.

Взаимно перпендикулярные плоскости. Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой. Следовательно, плоскость, перпендикулярная плоскости АВС, будет определяться отрезком DE и перпендикуляром к плоскости треугольника, проведенным через точку D или E. Прямая перпендикулярна плоскости, если ее проекции перпендикулярны одноименным проекциям горизонтали и фронтали.

Плоскость, проходящую через прямую DE и перпендикулярную плоскости АВС, ограничивают волнистой линией или отрезком.

Пересекающиеся плоскости. Пересечение плоскостей можно построить следующим способом: найти точки пресечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью. Для построения точки пересечения прямой с плоскостью общего положения надо выполнить следующее (рисунок 2):

1) через данную прямую (MN) провести некоторую вспомогательную фронтально-проецирующую плоскость (S),

2) построить прямую (1-2) пресечения плоскости данной (ABC) и вспомогательной (S),

3) определить положение точки (К) пересечения прямых – данной (MN) и построенной (1-2).

Определить видимость с помощью конкурирующих точек.

Рисунок 2 – Пересечение прямойс плоскостью

Построение следов плоскости. Каждый след плоскости представляет собой прямую линию, для построения которой необходимо определить две ее точки (одной из них может служить точка схода следов на оси проекций). Горизонтальный след плоскости определяется построением горизонтальных следов М и М двух прямых, принадлежащих данной плоскости. Фронтальный след плоскости можно построить с помощью определения одного фронтального следа прямой, поскольку второй точкой искомого следа может служить точка схода следов Р .

Параллельные плоскости. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Для выполнения задачи 3 необходимо построить точку, отстоящую от плоскости АВС на 4 см, и через нее провести две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости АВС.

Пример выполнения задания 1 приведен в приложении Б.

Задание 2. Пересечение гранных поверхностей.

Дана схема здания 20?15 м с четырехскатной крышей, угол наклона которой к горизонтальной плоскости проекций равен ?.

Требуется:

1. Вычертить вырез здания в М 1:100 (10?7,5 см), расположив его под углом ? к фронтальной плоскости проекций.

2. Взять точку S на расстоянии 5 м от середины плоскости ската P (точка А) и, приняв ее за вершину, построить правильную пирамиду с основанием в плоскости H (квадратное или треугольное) с углом наклона ребер 2:1, сторона основания пирамиды параллельна стороне выреза.

3. Построить пересечение пирамиды и выреза здания.

4. Определить следы плоскостей скатов крыш P и Q.

5. Построить тени на плоскостях H и V и на плоскостях скатов крыши.

Варианты задания приведены на рисунке 3 и в таблице 3.

Таблица 3– Варианты задания 2

Вариант	Основаниепирамиды	Угол?	Угол?	Вырез
	квадрат			I
	квадрат			II
	квадрат			I
	квадрат			II
	квадрат			I
	квадрат			II
	квадрат			I
	квадрат			II
	треугольник			I
	треугольник			II
	треугольник			I
	треугольник			II
	треугольник			I
	треугольник			II
	треугольник			I

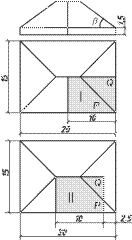
Рисунок 3 – Варианты выреза здания

Методические указания.Для выполнения задания необходимо проработать теоретические вопросы: перпендикулярность прямой и плоскости; натуральная величина отрезка; пересечение прямой и плоскости; пересечение гранных поверхностей; следы прямой и плоскости; тени точки, прямой, плоскости.

Работу начинают с определения высоты выреза схематического здания.

Чтобы найти вершину пирамиды S, надо через точку А провести перпендикуляр к плоскости ската Р и найти на нем точку, отстоящую от плоскости Р на 5 м.

Построение линии пересечения пирамиды и схематического здания можно произвести следующим способом: определить точки, в которых ребра пирамиды пересекают грани здания, и ребра здания пересекают грани пирамиды. Это задача на пересечение прямой с плоскостью (рисунок 2). Полученные точки, принадлежащие одним граням, соответственно соединяются. Линии построения сохраняют, обозначают основные точки. Видимость определяется с помощью конкурирующих точек.

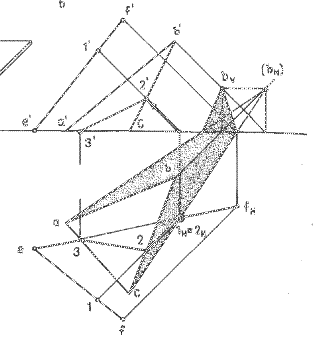Тени от пирамиды на скаты крыши строят с помощью способа обратных лучей. Контур падающих теней, закрытых зданием, не показывают. Падающие тени отмывают темнее собственных.

Способ обратных лучей.

Рисунок 4 – Способ обратных лучей

На рисунке 4показано построение падающей тени от прямой EF на плоскость треугольника ABCв ортогональных проекциях. Прежде всего строят падающие тени треугольника и прямой на плоскость Н. Точка 1Н =2Н является точкой пересечения контуров теней. Из этой точки проводят обратный луч до пересечения со стороной треугольника в точке 2,2´. Эта точка будет тенью от точки прямой на плоскость треугольника. Падающая тень прямой должна пройти от точки 3 к построенной точке 2,2′. Если продолжить обратный луч до пересечения с прямой EF, определим точку 1, которая бросает тень в точку 2 треугольника, а затем в точку 1 Н = 2Н на плоскости Н. Все три точки лежат на одном световом луче.

Пример выполнения задания приведен в приложении Б.

Задание 3. Пересечение поверхностей. Развертка.

Построить пересечение двух поверхностей, из которых первая – поверхность вращения с вертикальной осью, вторая – призматическая с ребрами, расположенными по направлению диагонали куба, грани которого параллельны плоскостям проекций (их проекции располагаются под углом 45° к оси проекций). Построить развертки частей поверхностей с нанесением линий пресечения.

Вариант задания выбирается согласно рисунку 5 и таблице 4.

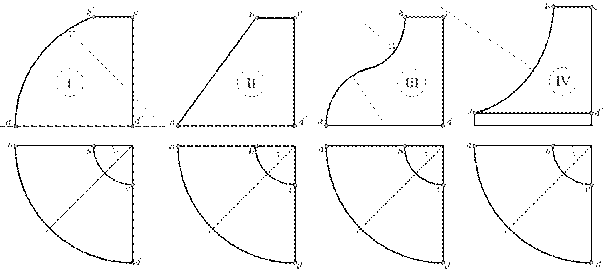
Рисунок 5 (начало) – Варианты задания 3

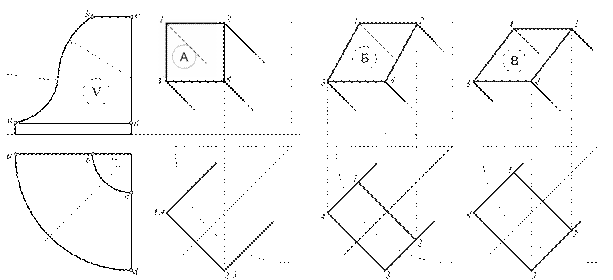
Рисунок 5 (окончание)

Таблица 4– Варианты задания 3

Вариант	Поверхность вращения	Граннаяповерхность
	I	А
	II	Б
	III	В
	IV	А
	V	Б
	I	В
	II	А
	III	Б
	IV	В
	V	А
	I	Б
	II	В
	III	А
	IV	Б
	V	В

Методические указания. Для выполнения задания необходимо проработать теоретические вопросы: пересечение поверхностей с применением посредников-плоскостей; развертка гранных поверхностей; развертка неразвертывающихся поверхностей.

Задачи на построение пересечения поверхностей и развертки гранного тела разместить на одном листе, задачу на построение развертки тела вращения – на другом.

Исходные данные увеличить в 3 раза.

Для тела вращения построить развертку только боковой поверхности, разделив ее на 4-5 лепестков, по принципу построения развертки сферической поверхности.

Развертка сферы может быть выполнена в следующем порядке (рисунок 6, а). Горизонтальную проекцию экватора разбивают на равное число частей, например, на восемь, и через полученные точки проводят горизонтальные проекции меридианов. Часть сферической поверхности, заключенную между смежными меридианами а и b, заменяют элементом цилиндрической поверхности Ф, касательной к сфере по главному меридиану m. Ось такой цилиндрической поверхности (ее очерк на рисунке показан тонкими линиями) проходит через центр сферы перпендикулярно к фронтальной плоскости проекций. Горизонтальной проекцией цилиндрического элемента является треугольник A l B . Затем строят развертку элемента цилиндрической поверхности. Для этого фронтальную проекцию главного меридиана m также разбивают на равное число частей (например, на восемь) и на вертикальной прямой от точки 5 , взятой на ней, откладывают отрезки 5 – 4 , 4 –3 и так далее, равные длине дуг 5 –4 , 4 –3 и так далее (рисунок 6, б). Через полученные точки проводят прямые, перпендикулярные к 1 –5 и на них откладывают длины образующих элемента цилиндрической поверхности. Так, от точки 5 отложены отрезки (5 –А )=(5–А) и (5 –В ) = (5 –B ), от точки 4 – (4 –Е ) = (4 –E ) и так далее. Соединив найденные таким образом точки лекальной кривой, получают плоскую фигуру, являющуюся приближенной разверткой части сферы.

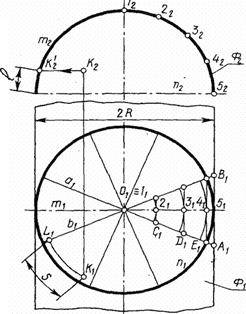
Рисунок 6 – Развертка сферической поверхности:а – аппроксимация сферических элементов цилиндрическими; б – развертка элемента цилиндрической поверхности

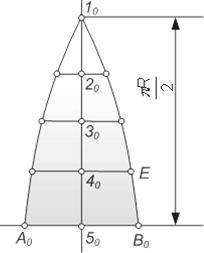Рисунок 4 – Развертка сферической поверхности

Положение произвольной точки K, принадлежащей сферической поверхности, может быть определено на развертке с помощью двух координат – длин дуг l и s. Дуга l определяет смещение точки К от экватора к полюсу, а дуга s – смещение ее от одного из меридианов по параллели сферы.

Развертка призматической поверхности может быть выполнена при помощи способа замены плоскостей проекций.

При построении пересечения поверхностей в качестве посредников целесообразно применить горизонтально-проецирующие плоскости, проведенные через ребра и между ребрами призматической поверхности, и использовать параллели поверхности вращения.

Обозначить основные точки, линию пересечения выделить другим цветом.

Пример выполнения задания приведен в приложении Б.

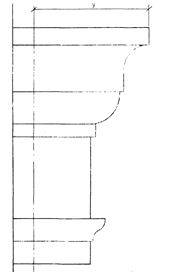
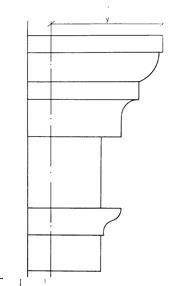
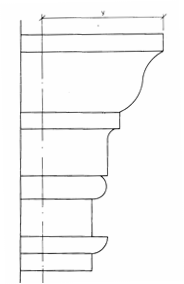
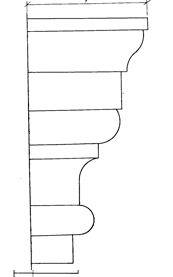
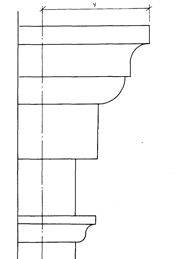
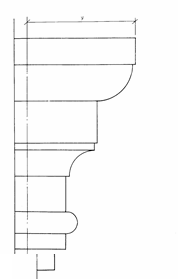
Задание 4. Построение теней архитектурных деталей.

Построить собственные и падающие тени капители способом лучевых сечений.

Варианты заданий приведены на рисунке 6.

Методические указания.Исходное задание увеличить в 3-4 раза.

Рекомендуется провести 5 лучевых плоскостей: Р — через угол плиты, Р — касательно к цилиндрической части, Р — касательно к валику и еще две — Р — между Р и Р , Р — между Р и Р (рисунок 6). Много плоскостей брать не рекомендуется.

При построении теней принимается условное освещение лучами, расположенными по направлению диагонали куба, грани которого параллельны плоскостям проекций, т.е. горизонтальная и фронтальная проекции лучей располагаются под углом 45° к оси проекций.

Все вспомогательные линии необходимо выполнять более жестким карандашом и обязательно сохранять на листе, полученные линии контуров теней следует несколько усилить более мягким карандашом. Обозначение основных точек на исходном чертеже и их теней обязательно.

Площадь теней выделить отмывкой, причем собственные тени будут светлее падающих.

1 2 3

4 5 6

7 8 9

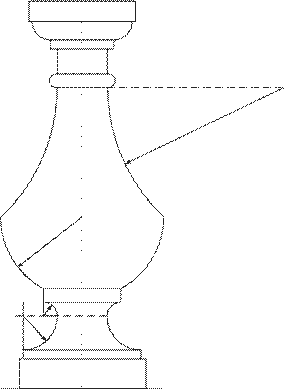
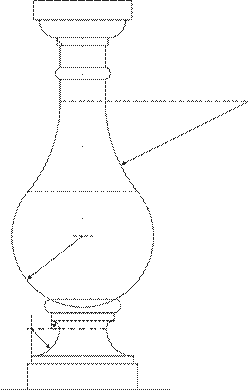
Задание 5. Построение теней балясины.

Построить собственные и падающие тени балясины.

Варианты задания приведены на рисунке 7.

Методические указания.Исходное задание увеличить в 2 раза.

Балясина выступает из плоскости стены на ½ ее диаметра.

Для построения светотени надо определить границы (контуры) собственных и падающих теней. Эта операция основана на построении линии прикосновения лучевой поверхности с данной поверхностью и определении линии пересечения поверхностей.

Граница падающей тени является тенью от границы собственной тени. К обеим границам должны быть касательны крайние лучи.

Построение теней балясины – это комплексная задача, для выполнения которой необходимо вспомнить построение теней таких фигур, как окружности, цилиндра, конуса, шара, валика, скоции.

Для построения собственных теней целесообразно применить способ касательных конусов, а для построения падающих теней – способ выноса (рисунок).

Если известен вынос точки у, т. е. расстояние от фронтальной плоскости, то тень может быть построена по этому выносу. От проекции точки а’ вправо по горизонтали откладывают величину выноса у; пересечение вертикали, проходящей через полученную точку а , с проекцией луча и дает тень А от точки А.

Обозначить основные точки, собственные тени отмыть светлее, чем падающие.

. Рисунок 5 – Способ

выноса

1 2

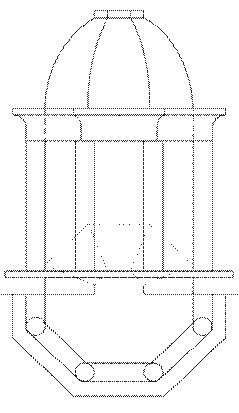
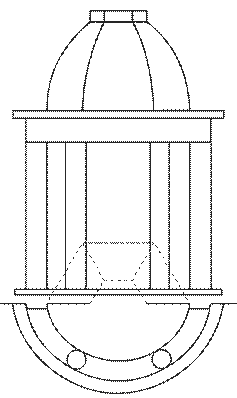
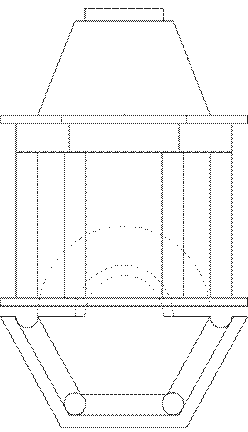
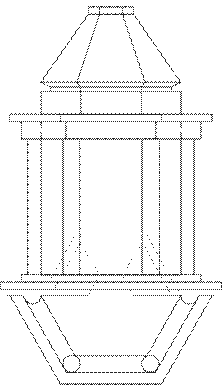
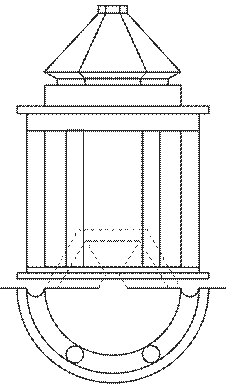
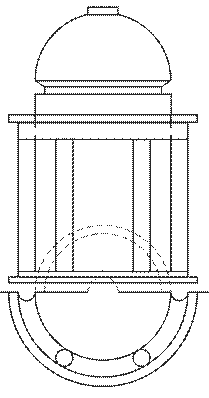
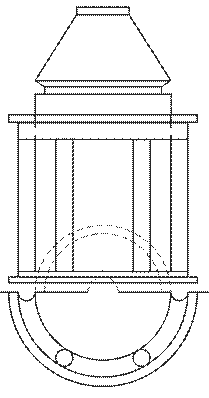
Задание 6. Тени портика.

Построить собственные и падающие тени портика.

Варианты задания приведены на рисунке 8.

Методические указания.Исходное задание увеличить в 2 раза.

1 2

3 4

5 6

7 8

Рисунок 8 (окончание)

Портик состоит из двух колонн и антаблемента, за которым находится ниша. Как портик, так и ниша имеют в плане форму гранную или в виде части окружности, верх ниши также гранной или криДля построения теней необходимо проработать теоретические вопросы: тени точки, прямой, окружности, тени в нишах.

Для облегчения вспомогательных построений часть плана, наложенного на фасад, рекомендуется вычертить на подложенной полоске бумаги, которую по окончании работы снять.

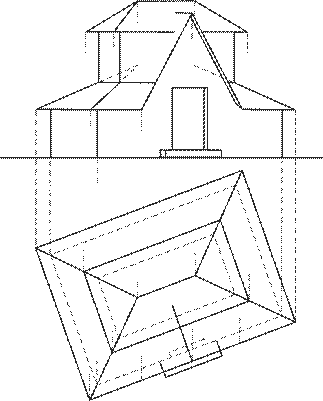
Задание 7. Аксонометрия. Тени в аксонометрии.

Построить тени на схеме здания, данного в повернутом положении по отношению к фронтальной плоскости. Тень на горизонтальную плоскость построить в предположении, что фронтальная плоскость отсутствует. Затем построить аксонометрию и тени в аксонометрии.

Варианты индивидуальных заданий приведены на рисунке 8.

Методические указания.Аксонометрию схематизированного здания вычертить на свободном поле чертежа. Оси аксонометрии принять параллельно основным ребрам здания.

Рекомендуется строить прямоугольную изометрию по размерам ортогонального чертежа. В прямоугольной изометрии все углы между осями равны 120º. Показатели искажений по всем осям равны единице. Изображение в прямоугольной изометрии обладает хорошей наглядностью, но объекты, приближающиеся к форме куба или имеющие квадратный план, в такой аксонометрии выполнять не рекомендуется, так как направление проецирования совпадает с одной диагональю куба, которая в изображении вырождается в точку. Можно построить объект в прямоугольной диметрии. Оси X и Y строят следующим образом: для оси Х – на горизонтальной прямой откладывают восемь равных отрезков, а в конце на вертикальной прямой откладывают один такой же отрезок и полученную точку соединяют с началом осей; для оси Y – соответственно на горизонтальной прямой откладывают восемь отрезков, а по вертикали – семь отрезков. Показатель искажения по оси Y принимают равным 0,5, по остальным осям – равным единице.

План здания (вторичную проекцию) вычертить полностью, поскольку она необходима для построения теней.

Для построения теней в аксонометрии задают направление лучей света и их вторичных проекций. Хороший результат получается, когда главный фасад освещен, а боковой находится в собственной тени. При этом направление проекций лучей не должно совпадать с направлением ни одной из аксонометрических осей.

Линии построения теней сохраняют. Контур падающих теней, закрытых зданием не показывают.

Рядом с аксонометрией обязательно указывают направление аксонометрических осей и выбранное направление лучей.

Пример выполнения задания приведен в приложении Д.

1 2

3 4

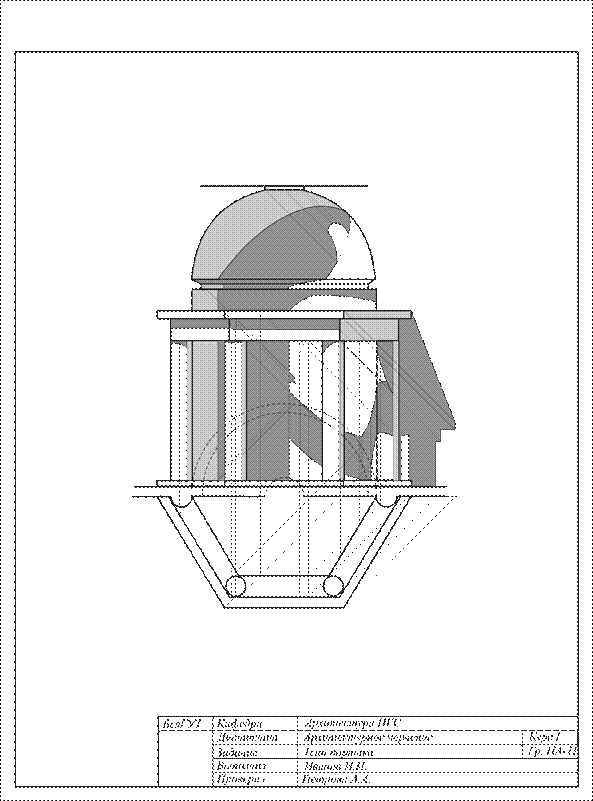
ПРИЛОЖЕНИЕ Г

(рекомендуемое)

Построение теней портика

ПРИЛОЖЕНИЕ Д

(рекомендуемое)

Статьи к прочтению:

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решение

Похожие статьи: