Операции (высказывания) алгебры логики
Основные понятия алгебры логики. Логические основы ЭВМ
Двоичная система счисления — позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).(стр 83-88 лучше все прочитать и попытаться понять)
Восьмери?чная систе?ма счисле?ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
В Ада и VHDL такие числа указывают так: «16#5A3#».
В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
Другие ассемблеры (ATT, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «h». Например, «h5A3».
В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
В электронных калькуляторах
Б3-34 и ему подобные используют -, L, C, Г, E (space) на их экране.
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·160+10·161+5·162
= 3·1+10·16+5·256 = 3+160+1280 = 144310
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | |||||||
| 1hex | = | 1dec | = | 1oct | |||||||
| 2hex | = | 2dec | = | 2oct | |||||||
| 3hex | = | 3dec | = | 3oct | |||||||
| 4hex | = | 4dec | = | 4oct | |||||||
| 5hex | = | 5dec | = | 5oct | |||||||
| 6hex | = | 6dec | = | 6oct | |||||||
| 7hex | = | 7dec | = | 7oct | |||||||
| 8hex | = | 8dec | = | 10oct | |||||||
| 9hex | = | 9dec | = | 11oct | |||||||
| Ahex | = | 10dec | = | 12oct | |||||||
| Bhex | = | 11dec | = | 13oct | |||||||
| Chex | = | 12dec | = | 14oct | |||||||
| Dhex | = | 13dec | = | 15oct | |||||||
| Ehex | = | 14dec | = | 16oct | |||||||
| Fhex | = | 15dec | = | 17oct | |||||||
Операции (высказывания) алгебры логики
Типы высказываний (основные операции алгебры логики):
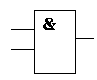
1. Конъюнкция – логическое умножение (результат соединения высказываний с помощью связки “и”) дает сложное высказывание, истинное только тогда, когда истинны оба составляющие его высказывания обозначаются: x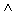 y или xy или х?у, читается “х и у”.
y или xy или х?у, читается “х и у”.
Обозначается Таблица истинности
на схемахлогического умножения
| X | Y | Х U Y |
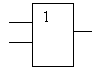
2. Дизъюнкция – логическое сложение (результат соединения высказываний с помощью связки ”или”) дает сложное высказывание, истинное, когда истинно хотя бы одно из составляющих его высказываний. Обозначается x 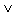 y или x + y – дизъюнкция, читается “х или у”
y или x + y – дизъюнкция, читается “х или у”
Обозначается Таблица истинности
на схемах 1 логического сложения
| X | Y | Х U Y |
3. Строгая дизъюнкция (результат соединения высказываний с помощью связки “исключающее или”) дает сложное высказывание, истинное, когда истинно только одно из составляющих его высказываний (x 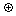 y или x
y или x 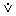 y — строгая дизъюнкция).
y — строгая дизъюнкция).
Таблица истинности
| X | Y | Х 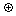 Y Y |
Иначе эта операция называется “сложение по модулю 2”, т.к. при сложении четного количества единиц результат будет 0, а при сложении нечетного количества единиц – 1.
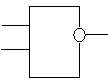
4. Инверсия — логическое отрицание (результат применения к высказыванию связки “не”) дает сложное высказывание, истинное, когда исходное высказывание ложно (  x или
x или 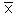 — инверсия).
— инверсия).
Обозначается инверсия Таблица истинности инверсии
| Х | 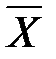 |
на схемах
| Нет |
5. Импликация (следование) (результат соединения высказываний с помощью связки “если … , то”) дает сложное высказывание, ложное, только когда первое из составляющих его высказываний истинно, а второе — ложно (x 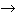 y — импликация).
y — импликация).
Таблица истинности
импликации
| Х | Y | X 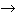 Y Y |
6. Эквиваленция (результат соединения высказываний с помощью связки “тогда и только тогда”) дает сложное высказывание, истинное, когда истинность составляющих его высказываний совпадает (X « Y или X º Y — эквиваленция).
Эта операция называется также “эквивалентность” или равнозначность. Ее таблица истинности
| Х | Y | X«Y |
Алгебра логики вводит аксиомы и основные законы, с помощью которых можно упростить схемную реализацию компьютерных устройств или алгоритмов обработки информации, тем самым повысить надежность и сократить затраты на обработку информации. Используются также логические операторы — кванторы общности 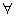 (“для всех”) и существования
(“для всех”) и существования 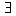 (“существует”). Для сложных высказываний строятся таблицы истинности, например:
(“существует”). Для сложных высказываний строятся таблицы истинности, например:
Статьи к прочтению:
- Операционная система windows xp поддерживает файловую систему … ntfs
- Операционные семейства windows. основные тенденции развития ос.
Лекция 3: Высказывания и действия над ними
Похожие статьи:
-
Логические элементы эвм. алгебра логики. законы алгебры логики.
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики или, как ее часто называют, булева…
-
Базовыми операциями алгебры логики
операции логического умножения – конъюнкции ( ), логического сложения – дизъюнкции ( ), исключающего или – (A), логического отрицания – инверсии ( )….
