Операторы, вычисляющие значение функции
endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction
Ниже приводится пример вычисления интеграла 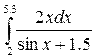 .
.
| Фрагмент программыfunction y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z) | Результат 30.437056 |
Для решения нелинейных уравнений в Scilab используется функция
fsolve(x0,f) ,
где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.
Например, для решения уравнения 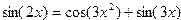 для начального приближения
для начального приближения 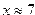 нужно выполнить следующие команды:
нужно выполнить следующие команды:
| Фрагмент программы deff(‘y=F(x)’, ‘y=sin(2*x)-cos(3*x.^2)-sin(3*x)’)root=fsolve(7,F)disp(root) | Результат 6.9755674 |
Для решения полиномиальных уравнений вида 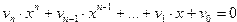 используется функция
используется функция
roots(a),
где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
Результатом работы этой функции будет вектор корней полинома размерностью n.
Пример решения полиномиального уравнения 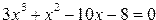 приведен ниже.
приведен ниже.
| Фрагмент программы v=[3 1 -10 -8]R=roots(v)disp(R) | Результат 2.- 1.3333333- 1. |
Для уравнения 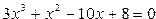 два корня – комплексные.
два корня – комплексные.
| Фрагмент программыv=[3 1 -10 8]R=roots(v)disp(R) | Результат- 2.29358350.9801251 + 0.4494650i0.9801251 — 0.4494650i |
Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения 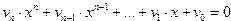 :
:
poly(a, x, f1 ),
где a –вектор коэффициентов полинома записанных в обратном порядке, x — символьная переменная, f1– символьная переменная, принимающая значения ‘c’ или ‘r’ (roots или coeff).
Например, чтобы создать полином 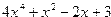 , нужно использовать команду
, нужно использовать команду
| Фрагмент программыp=poly([3 -2 1 0 4],’x’,’c’)disp(p) | Результат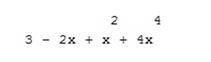 |
Для решения уравнения 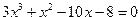 можно выполнить следующие команды:
можно выполнить следующие команды:
| Фрагмент программыp=poly([-8 -10 1 3],’x’,’c’)R=roots(p)disp(R) | Результат2.- 1.3333333- 1. |
Для решения систем линейных уравнений в Scilab есть следующие способы:
— применение операции левого матричного деления;
— использование обратной матрицы.
Если задана система линейных алгебраических уравнений вида:
AX=B,
где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:
Х=А \ B
То же самое решение может быть получено с помощью обратной матрицы, например:
X=inv(A)*B
Например, решить систему уравнений 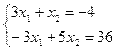
можно так:
| Фрагмент программыA=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)или X1=A\B , disp(X1) | Результат- 3.11111115.3333333 |
Для решения систем нелинейных уравнений можно использовать функцию
fsolve(x0,f),
где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему
Например, решение системы 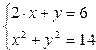 можно выполнить следующим образом:
можно выполнить следующим образом:
| Фрагмент программыfunction [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R) | Результат1.23380963.5323808 |
Практическая часть
Задание 1. Вычисление определенного интеграла
Статьи к прочтению:
Эмулятор кнопки DISP на БК Mitsubishi Space Star
Похожие статьи:
-
Типы данных. выражения. операторы. функции
В системе MATLAB определено шесть базовых типов данных, каждый из которых является многомерным массивом. Шесть классов — это double, char, sparse, uint8,…
-
Тип возвращаемого значения и параметры функции main
Функция main может иметь тип возвращаемого значения int (задает код возврата программы операционной системе, он может использоваться в пакетных командных…
