Построение безызбыточного кода шеннона-фано по методу хаффмена
Упражнение 1.
Оцените коэффициент избыточности (11). Для этого воспользуйтесь Программой «AnDynSys» (Вкладка «Характеристики ИД», Раздел «Гистограмма») и буквенной последовательностью « Kovalev-Husserl» из Папки «Числовые последовательности».
Введите Числовую последовательность из Папки в качестве Файла во Вкладку «Обработка исходных данных».
Для идентификации букв и других знаков русского языка воспользуйтесь «Материалом к Упражнению 1». Для настройки Программы в этом Материале даны Указания.
Согласно Указаниям рассчитайте Гистограмму.
Выпишите из Раздела «Гистограмма» под графиком числовую таблицу распределения вероятностей букв и других знаков русского языка. Подставьте взятые из таблицы вероятности в формулу (7). Объем сообщения вычислите по формуле (5). Для данного примера L = 40 . При вычислении по формуле (5) следует округлять J до ближайшего целого сверху. Затем примените формулу (11).
Контролем правильности расчетов является выполнение условия
p1 + p2 + … + pL = 1.
Упражнение 2
Построение безызбыточного кода Шеннона-Фано по методу Хаффмена
1.Изучите метод кодирования, изложенный ниже.
2.Задайте собственный набор вероятностей, при условии, что их сумма по-прежнему равна единице.
3. Постройте собственный безызбыточный код.
4.Вычислите среднюю длину своего кода по формуле (12) и коэффициент
к/к ср . Сравните со значениями, приведенными ниже. Ваши выводы?
Идея заключается в том, чтобы те буквы, которые встречаются чаще, кодировать меньшим числом двоичных символов – так, чтобы среднее число символов на букву стало меньше пяти, желательно равным количеству информации в символе. Тогда объем сообщения сравняется с количеством информации.
Техническим воплощением идеи является код Шеннона – Фано. Простая процедура построения этого кода, предложенная Д.А.Хаффменом, иллюстрируется Табл.1
Таблица 1
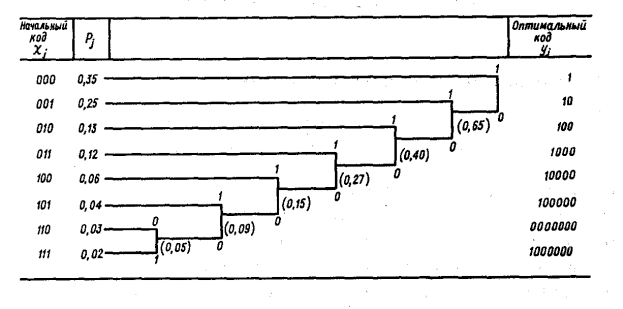
и состоит в следующем.
1.Расположим буквы в порядке убывания их априорных вероятностей.
2.Выберем две наименее вероятные буквы. Одной из них (с меньшей вероятностью) присвоим в составляемом коде символ «1», другой – «0». Это будут самые младшие символы (стоят в начале будущего кода).Обе вероятности просуммируем, сумму внесём в список вместо двух прежних (см. нижнюю строку таблицы 1).
3.В исправленном списке снова выберем две наименьшие вероятности. Соответствующим буквам присвоим символы 0 и 1 в следующей позиции составляемого кода. Вероятности просуммируем, внесём в список и т.д., пока не исчерпается последний исправленный список. Пример в табл.1 составлен для алфавита из 8 букв. Исходные коды букв – в первой колонке, полученные оптимальные коды – в последней.
Длина исходного кода для всех букв одинакова и равна к = 3. Средняя длина оптимального кода
кср = к1р1 + к2 р2 + …+ к8 р8 = 2,6. (12)
Объём сообщения уменьшился в к / кср = 3 / 2,6 = 1,15 раз.
Если кодировать не отдельные буквы, а слова или блоки из n последовательных слов (nк двоичных символов), то выигрыш растет с увеличением длины блока. На таком принципе построены многие применяемые коды, обеспечивающие сжатие объема сообщения до 2-х раз.
Упражнение 3.
Компьютерный эксперимент
Статьи к прочтению:
- Построение диаграмм и графиков
- Построение диаграмм и графиков. в программе excel термин диаграмма используется для обозначения всех видов графического представления числовых данных
Метод Шеннона-Фано
Похожие статьи:
-
Дерево вывода. методы построения дерева вывода
Деревом вывода грамматики G(VT,VN,P,S) называется дерево (граф), которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям: …
-
Методы эффективного кодирования некоррелированной последовательности знаков, код шеннона-фано
Введение Важнейшей частью информатики как науки является теория информации, которая занимается изучением информации как таковой, ее появлением, развитием…
