Построение нисходящего автомата
Рассмотренные понятия и методы их использования приводят к небольшой корректировке правил порождения АМП по S-грамматике, чтобы получить процедуру создания автомата по q-грамматике. Эта корректировка касается только пункта 5. Можно, конечно, полностью переписать исправленный алгоритм создания автомата, но лучше воспользуемся авторским текстом [16]. Пятое правило заменяется двумя следующими:
5.1. Правило грамматики применяется всякий раз, когда магазинный символ является его левой частью, а входной символ принадлежит его множеству выбора. Для того чтобы применить правило вида:
Ab?,
используется переход:
Заменить (?r), Сдвиг
Если правило имеет вид:
Ab,
то используется:
Вытолкнуть, Сдвиг.
Для того чтобы применить правило:
Ae
используется переход
Вытолкнуть.
5.2. Если имеется правило с нетерминалом A в левой части и элемент, соответствующий магазинному A и входному символу b не был создан по правилу 5.1, то таким элементом может быть или применение пустого правила (A? ) или операция «Отвергнуть».
Примеры построения АМП по q-грамматике
Построим автомат с магазинной памятью по q-грамматике, используемой выше для различных иллюстраций. Его таблица переходов будет иметь следующий вид.
| Магазинные символы | Входные символы | |||
| a | b | c | + | |
| S | ¦ SA, | ^, | Отвергнуть | Отвергнуть |
| A | ^ | ^ | ¦ SA, | Отвергнуть |
| N | Отвергнуть | Отвергнуть | Отвергнуть | Допустить |
Следующий пример иллюстрирует использование правила 5.2, когда описанное в нем ячейка таблицы переходов может быть реализована любым из двух вариантов (для определенности выберем второй). Грамматика G9.5(S) описывается следующими правилами:
1. SaA
2. Sb
3. AcSa
4. Ae
Множества выбора для каждого из правил будут выглядеть следующим образом:
ВЫБОР(1) = ВЫБОР (SaA) = {a}
ВЫБОР(2) = ВЫБОР (Sb) = {b}
ВЫБОР(3) = ВЫБОР (AсSa) = {c}
ВЫБОР(4) = ВЫБОР (Ae) = СЛЕД (A) = {a, 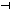 }
}
Полученные данные использованы для построения таблицы переходов. Ячейка, содержащая альтернативные правила, находится на пересечении строки с магазинным символом A и столбце с входным символом b.
| Магазинные символы | Входные символы | |||
| a | b | c | + | |
| S | ¦ A, | ^, | Отвергнуть | Отвергнуть |
| A | ^ | 1)^или 2)Отвергнуть | ¦ aS, | ^ |
| a | ^, | Отвергнуть | Отвергнуть | Отвергнуть |
| N | Отвергнуть | Отвергнуть | Отвергнуть | Допустить |
Для того чтобы проверить, как действуют эти правила, необходимо ввести неправильную цепочку. Возьмем, например, цепочку ab. В первом случае используем выталкивание, которое ведет к отвержению цепочки на третьем шаге.
| Номер шага | Содержимое стека | Остаток входной цепочки | Применяемый переход | Комментарий |
| NS | ab+ | ¦ A, | ||
| NA | b+ | ^ | Использовано выталкивание | |
| N | b+ | Отвергнуть | Все равно отвергли |
Во втором варианте цепочка отвергается уже на втором шаге.
| Номер шага | Содержимое стека | Остаток входной цепочки | Применяемый переход | Комментарий |
| NS | ab+ | ¦ A, | ||
| NA | b+ | Отвергнуть | На шаг раньше |
Статьи к прочтению:
Лекция 298.Введение в цифровые автоматы
Похожие статьи:
-
Построение автомата с магазинной памятью по q-грамматике
Контекстно-свободная грамматика называется q-грамматикой тогда и только тогда, когда выполняются два условия: 1. Правая часть каждого правила либо…
-
И автоматами с магазинной памятью
Эта связь давно доказана и рассмотрена в специальной литературе для различных классов грамматик и методов разбора. В рамках данной дисциплины можно…
