Простейшие типовые звенья систем регулирования
Звеном системы называется ее элемент (часть), обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь самую разнообразную физическую основу (электрические, гидравлические, механические и т.д.) и конструктивное исполнение, но при этом относиться к одной функциональной группе. Соотношение входного и выходного сигналов в звеньях одной и той же группы описываются одинаковыми дифференциальными уравнениями. Это свидетельствует о том, что такие звенья имеют одинаковые динамические свойства. Так как процесс автоматического регулирования определяется только динамическими свойствами системы, то в основу классификации звеньев положены их динамические свойства.
Простейшими типовыми звеньями АСР являются: усилительное, интегрирующее, апериодическое, колебательное, запаздывающее и дифференцирующее звенья.
а) Усилительное звено
В усилительном звене выходная величина в каждый момент времени пропорциональна входной величине
Хвых = k • Xвх (2.1)
Коэффициент пропорциональности k называется коэффициентом усиления или коэффициентом передачи звена. Уравнение усилительного звена (2.1) – алгебраическое. Это свидетельствует о том, что усилительное звено передает сигнал мгновенно без динамических переходных процессов и искажений.
Передаточная функция звена имеет вид:
H(p) = k (2.2)
Примерами усилительных звеньев могут служить механические передачи, потенциометрические датчики, безинерционные усилители и т.п.
б) Интегрирующее звено
Выходная величина интегрирующего звена пропорциональна интегралу входной величины
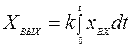 (2.3)
(2.3)
Коэффициент k называется коэффициентом передачи звена по скорости изменения выходной величины при единичном значении входной величины.
Передаточная функция звена имеет вид:
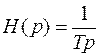 (2.4)
(2.4)
Величина Т называется постоянной времени интегрирующего звена
в) Апериодическое звено
Передаточная функция апериодического звена
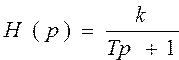 (2.5)
(2.5)
Кривые переходных процессов имеют вид экспонент. Апериодическое звено часто называют инерционным звеном 1-го порядка. Величина Т называется постоянной времени. Постоянная времени определяет динамические свойства звена. Чем она больше, тем медленнее протекает переходный процесс в звене и наоборот.
г) Колебательное звено
Передаточная функция колебательного звена имеет вид:
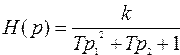 (2.6)
(2.6)
При T1/T22 переходный процесс определяется двумя компонентами и в этом случае диффереренциальное уравнение характеризует переходные процессы соединения, состоящего из двух соединенных последовательно апериодических звеньев. Следовательно, при T1/T22 нет необходимости вводить понятие нового типового звена, хотя на практике часто такое звено называют апериодическим звеном 2-го порядка. При T1/T2 = 0 переходный процесс периодический. При T1/T22 переходный процесс представляет собой затухающую синусоиду, амплитуда которой убывает по экспоненциальному закону. Таким образом переходные процессы колебательного звена зависят от соотношений постоянных времени Т1 и Т2.
д) Дифференцирующее звено
Передаточная функция дифференцирующего звена имеет вид:
Н(p) = k ? p (2.7)
Если выходные величины имеют одинаковую размерность. то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называют постоянной времени дифференцирующего звена.
е) Запаздывающее звено
Передаточная функция запаздывающего звена имеет вид:
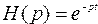 (2.8)
(2.8)
Статьи к прочтению:
Типовые звенья
Похожие статьи:
-
Стабилизация изменением параметров усилителя и звена осн
В принципе теперь уже можно переходить к коррекции замкнутой САР, поскольку формально устойчивость разомкнутого контура обеспечена с запасом в 6 дБ….
-
Типовая архитектура микропроцессорной системы
Федеральное агентство железнодорожного транспорта Государственное образовательное учреждение Высшего профессионального образования ПЕТЕРБУРГСКИЙ…
