Расчёт максимального порядка дифракционного спектра, угловой дисперсии и разрешающей способности дифракционной решётки

1. Оцените теоретическое значение максимально возможного числа главных интерференционных максимумов, даваемое используемой дифракционной решёткой и сравните с экспериментально наблюдаемой дифракционной картиной.

Наибольший порядок спектра дифракционной решётки можно найти из условия главного максимум

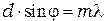откуда следует:

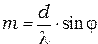. (2)

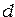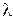Из формулы (2) видно, что максимальный порядок дифракции для заданных и определяется значением переменной величины 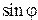. Наибольшее значение 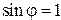, следовательно:

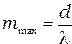(3)

2. Рассчитайте угловую дисперсию дифракционной решётки.

По определению угловой дисперсией называется величина

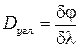
где 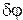угловое расстояние между спектральными линиями, отличающимися по длине волны на 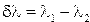. Дисперсию можно определить из условия главного максимума

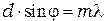Чтобы найти угловую дисперсию дифракционной решётки, продифференцируем левую часть условие главного максимума по углу 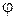, а правую по 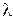. Опуская знак минус в левой части, получим:

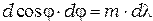
Отсюда:

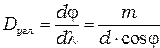. (4)

При малых углах дифракции 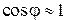, поэтому можно положить

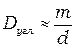(5)

Из полученного выражения следует, что угловая дисперсия обратно пропорциональна периоду решётки 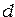. Чем выше порядок спектра , тем больше дисперсия.

3. Определите разрешающую силу дифракционной решётки.

Разрешающая способность дифракционной решётки определяется по формуле:

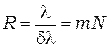(6)

где — порядок максимума, 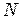— число щелей, участвующих в формировании дифракционной картины. В нашем случае:

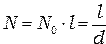где 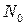— число щелей на единицу длины дифракционной решётки ( 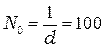шт./мм.); 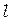— длина дифракционной решётки. Тогда разрешающая способность дифракционной решётки определяется формулой:

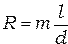
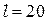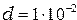Для оценки положим мм, мм.

4. Определите минимальную разность двух волн 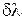соответствующей разрешающей способности.

Минимальная разность двух волн 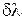, соответствующая разрешающей способности найдём по формуле (5)

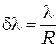(8)

ЛАБОРАТОРНАЯ РАБОТА № 3.14Г ДИФРАКЦИЯ ФРЕНЕЛЯ И ДИФРАКЦИЯ ФРАУНОФЕРА

Цель работы – Наблюдение дифракции Френеля и дифракции Фраунгофера на щели, на круглом отверстии и препятствиях различной формы.

Оборудование – Гониометр ГС-5, набор экранов.

Методика эксперимента

Работа выполняется на гониометре Г5 (ГС-5) — точном оптико-механическом приборе для отсчёта углов с ошибкой не более 2 (см. Приложение 2).

За счёт использования оптической системы (двух зрительных труб) фактическое расстояние 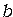от поверхности волнового фронта до точки наблюдения дифракции и от точечного источника до препятствия 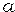дающего дифракцию значительно больше наблюдаемого. Это позволяет значительно уменьшить размеры экспериментальной установки и даёт возможность в широких пределах изменять к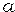ак так .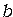

При перемещении окуляра маховичком 5 точка 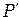, совпадающая с его фокусом, смещается, что позволяет наблюдать дифракционные картины, соответствующие различным значениям .

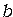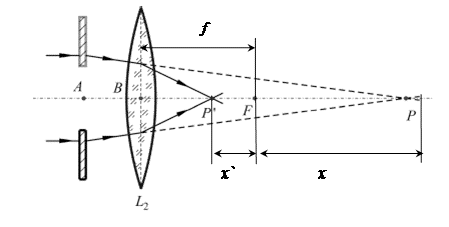
Рис. 1. Схема хода лучей за отверстием и объективом.

На рис. 1 представлена схема, с помощью которой можно рассчитать 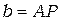, зная расстояние 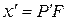— расстояние, на которое смещается окуляр. Точка F — фокальная точка объектива L2. Из геометрической оптики известна формула Ньютона, связывающая расстояния от плоскости изображения до фокальной плоскости с фокусным расстоянием :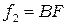

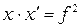(2)

Если 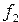и АВ не очень велики, то 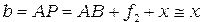. Тогда из (2):

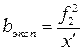(3)

Подставив это значение 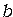в (5.5) 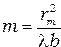и полагая, что 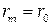получим экспериментальную зависимость числа зон Френеля укладывающихся в отверстии радиуса при изменении

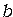
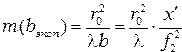(4)

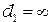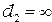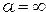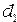Случай, когда на шкалах зрительных труб установлены значения и , соответствует условия и , т.е. условию наблюдения дифракции Фраунгофера. Все остальные значения и 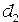соответствуют условию наблюдения дифракции Френеля.