Решение задач из тетради проектов

Основным содержанием данного проекта является решение задач из тетради проектов. Именно в ходе этой работы ребята должны усвоить правила проведения турниров (кругового и кубкового) и научиться оформлять их результаты в виде турнирной таблицы или дерева.

Задача 2.В этой задаче ребята увидят две таблицы для одного кругового турнира. Действительно, таблицу кругового турнира можно составлять по-разному. Так, по таблице 1 проще подсчитывать заброшенные шайбы (сумма чисел в соответствующей строке) и пропущенные шайбы (сумма чисел в соответствующем столбце). По таблице 2 проще подсчитывать набранные очки и выяснять места для каждой команды. Вот заполненные таблицы 1 и 2:

Таблица 1.

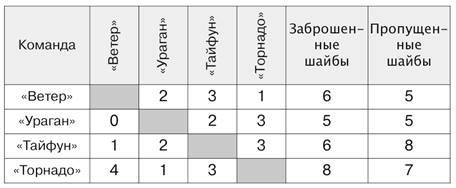
Таблица 2.

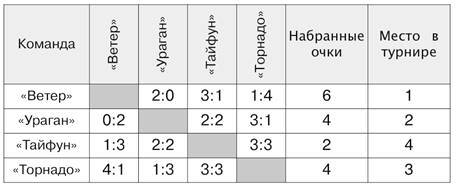
При заполнении таблицы 2 ребята столкнутся со сложным случаем распределения мест. Команды «Ураган» и «Торнадо» имеют по 4 очка. Команда «Ураган» при этом заняла более высокое (второе) место, поскольку выиграла во встрече с командой «Торнадо» (со счётом 3:1).

Задача 3. Эта задача снова посвящена круговому турниру, только команд в нём участвует гораздо больше, и это затрудняет работу с турнирными таблицами. Эта задача сложнее предыдущей ещё и тем, что придётся использовать одновременно информацию из двух таблиц. Кроме того, для решения необходимо понимать взаимосвязь и правила построения обеих таблиц. Лучше начать с того, что в обеих таблицах заполнить первые 8 столбцов (со счётом). Например, первая строка таблицы 4 позволяет заполнить первую строку и первый столбец таблицы 3 — записать заброшенные и пропущенные шайбы командой 3 «А» класса. После этого можно заполнить все остальные пустые клетки в таблицах. Мы приводим здесь заполненные таблицы 3 и 4:

Таблица 3.

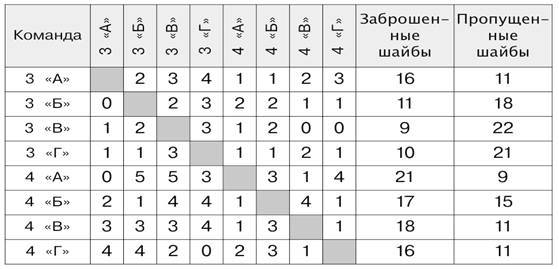
Таблица 4.

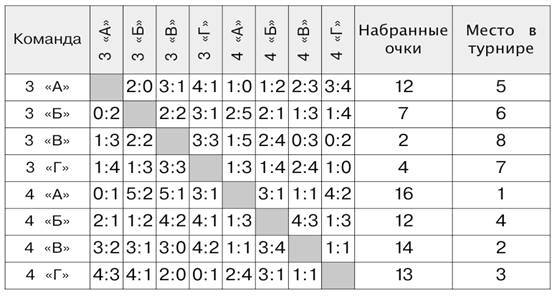
Кроме заполнения таблиц, ребята должны ответить на вопросы. Ответ на первый вопрос можно найти разными способами. Один из вариантов — вычислить при помощи рассуждений. Каждая из 8 команд играла с каждой из оставшихся 7 команд, значит, надо перемножить 7 и 8. Но при этом каждый матч был посчитан дважды, поэтому результат надо разделить на 2, и получится число игр. Другой вариант — просто сосчитать число клеток со счётом, которые располагаются выше диагонального ряда (или сосчитать все клетки со счётом, кроме диагональных, и разделить результат на 2).

Ответ на второй вопрос задачи можно найти в таблице 4, а на третий — в таблице 3.

Задача 4. Эта задача посвящена кубковому турниру. Здесь ребята смогут убедиться, насколько быстрее его проводить и легче подводить итоги. Фактически итоги подводятся автоматически, ведь итогом такого турнира является победа в самой последней игре. Результаты всех игр при решении этой задачи ребята будут брать из таблицы 4 (задачи 3). Например, в игре между командами 3 «А» и 4 «А» выиграл 3 «А», значит, команда этого класса и вышла в следующий тур, а в вершину дерева, предыдущую перед парой 3 «А» и 4 «А», надо записать 3 «А».

Сравнивая результаты решения этой и предыдущей задач, ребята могут убедиться, что в турнирах, проводимых по разным системам, могут быть разные победители — даже при одинаковых результатах игр. Так, в кубковом турнире уже в первом круге выйдет из борьбы победитель кругового турнира — 4 «А» класс. В результате победителем кубкового турнира становится 4 «В» класс.

Задача 5. В этой задаче ребята могут увидеть, что при проведении кубкового турнира победа одного из участников в значительной степени зависит от распределения участников по парам. Так, даже при очень стабильной игре в каждой паре игроков (как в данном случае) победитель турнира меняется в зависимости от того, как игроки расставлены в пары.

Идея решения этой задачи довольно проста. Если необходимо, чтобы выиграл Володя, ни в каком туре не надо его ставить в пары с игроком, которому он проигрывает — Колей. В частности, надо позаботиться о том, чтобы Коля не вышел во второй тур, и поставить его в первом туре играть с Петей. Аналогично ситуация будет складываться при выполнении второго задания. Что касается третьего задания, выполнить его невозможно, ведь Коля выигрывает только у одного игрока, а для победы ему надо сыграть две партии.

Проект «Турниры и соревнования». 2 часть

Статьи к прочтению:

15 СУМАСШЕДШИХ Ответов в Школьных Тетрадях!

Похожие статьи: