Сумма событий. теорема сложения вероятностей для несовместных событий
Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. По другому: суммой А + В двух событий А и В называют событие, состоящее в появлении хотя бы одного из этих событий.
В частности, если два события А и В — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого.
Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Пусть события А и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие А, либо событие В?
Ответ на этот вопрос дает теорема сложения вероятностей несовместных событий.
Теорема. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
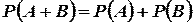 .
.
Доказательство. Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих .событию А; m2 — число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,
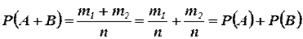 ,
,
так как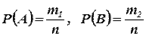 . Чтд.
. Чтд.
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
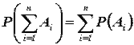 .
.
Пример. В урне 30 шаров: 10 красных, S синих я 15 белых. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие А)
Р (А) = 10/30= 1/3.
Вероятность появления синего шара (событие В)
Р(В)= 5/30 =1/6.
События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.
Искомая вероятность
P(A+B) = P(A) + P(B) = 1/3+1/6= 1/2.
Теорема. Сумма вероятностей событий А1, А2, … , Аn, образующих полную группу, равна единице:
P(A1) + P(A2) + … + P(An) = 1.
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать 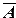 .
.
Пример. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то 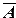 — промах.
— промах.
Теорема. Сумма вероятностей противоположных событий равна единице:
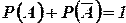 .
.
Замечание 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы p + q = 1
Пример. Вероятность того, что день будет дождливым р = 0,7. Найти вероятность того, что день будет ясным.
Решение. События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность q = 1 – p = 1 – 0,7 = 0,3.
Замечание 2. При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность события 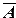 , а затем найти искомую вероятность по формуле
, а затем найти искомую вероятность по формуле
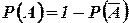 .
.
Пример. В ящике имеется n деталей, из которых m стандартных. Найти вероятность того, что среди k наудачу извлеченных деталей есть хотя бы одна стандартная.
Решение. События «среди извлеченных деталей есть хотя бы одна стандартная» и «среди извлеченных деталей нет ни одной стандартной» -противоположные. Обозначим первое событие через А, а второе — через 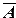 .
.
Очевидно,
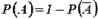 .
.
Найдем 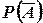 . Общее число способов, которыми можно извлечь k деталей из n деталей, равно
. Общее число способов, которыми можно извлечь k деталей из n деталей, равно 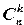 . Число нестандартных деталей равно n — m; из этого числа деталей можно
. Число нестандартных деталей равно n — m; из этого числа деталей можно 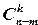 способами извлечь k нестандартных деталей. Поэтому вероятность того, что_среди извлеченных k деталей нет ни одной стандартной, равна
способами извлечь k нестандартных деталей. Поэтому вероятность того, что_среди извлеченных k деталей нет ни одной стандартной, равна 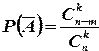 .
.
Искомая вероятность
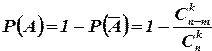
Коэффициент корреляции
Корреляционный анализ занимается степенью связи между двумя переменными, x и y.
Сначала предполагаем, что как x, так и y количественные, например рост и масса тела. Предположим, пара величин (x, у) измерена у каждого из n объектов в выборке.
Мы можем отметить точку, соответствующую паре величин каждого объекта, на двумерном графике рассеяния точек.
Обычно на графике переменную x располагают на горизонтальной оси, а у — на вертикальной. Размещая точки для всех n объектов, получают график рассеяния точек, который говорит о соотношении между этими двумя переменными.
Статьи к прочтению:
- Существует 7 шагов, которые помогут вам стать более уверенными.
- Sysprep.exe /generalize /oobe /reboot
16 Теорема сложения вероятностей совместных событий
Похожие статьи:
-
Центральная предельная теорема теории вероятностей.
Моделирование непрерывных случайных величин на ЭВМ. Цель работы. Моделирование различных типов непрерывных случайных величин в среде SciLab на основе…
-
События и обработчики событий в vba.примеры
Какое свойство объекта описывается в Height, Width №4 События и обработчики событий в VBA.Примеры 2.Какие свойства ячейки описывают Interior, Color,…
