Типы данных. выражения. операторы. функции
В системе MATLAB определено шесть базовых типов данных, каждый из которых является многомерным массивом. Шесть классов — это double, char, sparse, uint8, cell, и struct. Двумерные версии этих массивов называются матрицами, откуда MATLAB и получил свое имя МАТричная ЛАБоратория.
Диаграмма принадлежности того или иного объекта системы MATLAB к одному из классов имеет следующий вид (рисунок. 3.26):
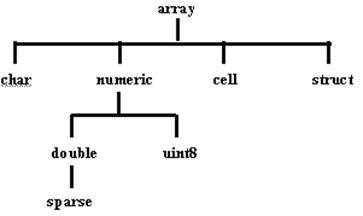
Рисунок 3.26 Диаграмма принадлежности объектов к одному из классов
Чаще всего пользователям приходится иметь дело только с двумя из этих типов данных: массив чисел удвоенной точности (double) и массив символов (char), или просто строка. Это связано с тем, что все вычисления в системе MATLAB выполняются с удвоенной точностью и большинство функций работают с массивами чисел удвоенной точности или строками.
Другие типы данных предназначены для таких специальных приложений, как работа с разреженными матрицами (sparse), обработка изображений (uint8), работа с массивами большой размерности (cell и struct).
Нельзя задать тип переменной numeric или array. Эти типы называются виртуальными и служат только для того, чтобы сгруппировать переменные, которые имеют общие атрибуты.
Тип uint8 предназначен для эффективного хранения данных в памяти. К данным этого типа можно применять только базовые операции индексации и изменения размеров, но нельзя выполнить никакой математической операции. Для этого такие массивы необходимо преобразовать в тип double.
Пользователь имеет возможность создания собственных типов и добавления методов для встроенных типов. Нижеприведенная таблица содержит седьмой тип данных — UserObject. Язык MATLAB позволяет создавать собственные типы данных и работать с ними по аналогии со встроенными типами.
Для встроенных типов данных можно переопределять метод точно также, как это делается для объекта. Например, чтобы задать операцию сортировки для массива типа uint8, необходимо создать метод (sort.m или sort.mex) и поместить его в специальный каталог @uint8.
В таблице 3.2 приведены все типы данных, определенных в MATLAB.
Таблица 3.2 Типы данных
| Класс | Пример | Описание |
| Double | [12;34] 5 + 6i | Числовой массив удвоенной точности (это наиболее распространенный тип переменной в системе MATLAB |
| Char | ‘Привет’ | Массив символов (каждый символ — длиной 16 битов), часто именуется строкой. |
| Sparse | Speye(5) | Разреженная матрица удвоенной точности (только двумерная). Разреженная структура применяется для хранения матриц с небольшим количеством ненулевых элементов, что позволяет использовать лишь небольшую часть памяти, требуемой для хранения полной матрицы. Разреженные матрицы требуют применения специальных методов для решения задач. |
| Cell | (17 ‘привет’ eye (2)) | Массив ячеек. Элементы этого массива содержат другие массивы. Массивы ячеек позволяют объединить связанные данные, возможно различных размеров, в единую структуру. |
| Struct | A.day = 12; A.color = ‘Red’; A.mat = magic(3); | Массив записей. Он включает имена полей. Поля сами могут содержать массивы. Подобно массивам ячеек, массивы записей объединяют cвязанные данные и информацию о них. |
| Uint8 | Uint8 (magic (3)) | Массив 8-разрядных целых чисел без знаков. Он позволяет хранить целые числа в диапазоне от 0 до 255 в 1/8 части памяти, требуемой для массива удвоенной точности. Никакие математические операции для этих массивов не определены. |
| UserObject | inline(‘sin(x)’) | Тип данных, определяемый пользователем |
Как и большинство других языков программирования, MATLAB предоставляет возможность использования математических выражений, но в отличие от многих из них, эти выражения в MATLAB включают матрицы.
Основные составляющие выражения:
— переменные
— числа
— операторы
— функции
Переменные
В MATLAB нет необходимости в определении типа переменных или размерности. Когда MATLAB встречает новое имя переменной, он автоматически создает переменную и выделяет соответствующий объем памяти. Если переменная уже существует, MATLAB изменяет ее состав и если что необходимо выделяет дополнительную память. Например,
d = 25
создает матрицу 1×1 с именем d и сохраняет значение 25 в ее единственном элементе.
Имена переменных состоят из букв, цифр или символов подчеркивания. MATLAB использует только первые 31 символ имени переменной.
MATLAB чувствителен к регистрам, он различает заглавные и строчные буквы. Потому А и а не одна и та же переменная.
MATLAB использует принятую десятичную систему счисления, с необязательной десятичной точкой и знаками плюс-минус для чисел. Научная система счисления использует букву «е» для определения множителя степени десяти. Мнимые числа используют i или j как суффикс. Некоторые примеры правильных чисел приведены ниже

Все числа для хранения используют формат long, определенный стандартом плавающей точки IEЕЕ. Числа с плавающей точкой обладают ограниченной точностью — приблизительно 16 значащих цифр и ограниченным диапазоном приблизительно от 10-308 до 10308 .
Операторы
Операторы – это неотъемлемая часть математических выражений, вычисление которых является одной из основных задач MATLAB как системы, созданной для выполнения численных расчетов
Выражения используют обычные арифметические операции и правила старшинства.
| + | сложение |
| — | вычитание |
| * | умножение |
| / | деление |
| \ | левое деление |
| ^ | степень |
| ‘ | комплексно сопряженное транспонирование |
| ( ) | определение порядка вычисления |
Приоритет в выполнении арифметических операций обычный: сначала — возведение в степень, затем — умножение и деление, и потом — сложение и вычитание. Операции одинакового приоритета выполняются в порядке слева направо, но круглые скобки могут изменить этот порядок.
Помимо арифметических операций используются ещё операции отношения и логические операции.
Операции отношения сравнивают между собой два операнда по величине. Эти операции записываются следующими знаками или комбинациями знаков:
| меньше | |
| меньше или равно | |
| больше | |
| = | больше или равно |
| == | равно |
| ~= | не равно |
Последней группой операций являются логические операции:
| И | |
| | | ИЛИ |
| ~ | НЕ |
Логические операции трактуют свои операнды как истинные (не равные нулю) или ложные (равные нулю). Если оба операнда операции И истинны (не равны нулю), то результат этой операции равен 1 (истина); во всех остальных случаях операция И вырабатывает значение 0 (ложь). Операция ИЛИ вырабатывает 0 (ложь) только в случае, когда являются ложными (равными нулю) оба операнда. Наконец, операция НЕ инвертирует ложь на истину и наоборот. То есть, если её операндом является ненулевое число, то эта операция вырабатывает 0, а если операнд нулевой, то тогда результатом применения операции НЕ будет единица.
Логические операции имеют самый низший приоритет.
В одном и том же выражении можно использовать все перечисленные операции: арифметические, логические и операции сравнения. Последовательность выполнения операций определяется их расположением внутри выражения, их приоритетом и наличием круглых скобок.
Функции
MATLAB предоставляет большое количество элементарных математических функций, таких как abs, sqrt, exp, sin. Вычисление квадратного корня или логарифма отрицательного числа не является ошибкой: в этом случае результатом является соответствующее комплексное число. MATLAB также предоставляет и более сложные функции. Большинство из этих функций имеют комплексные аргументы.
Некоторые функции, такие как sqrt и sin — встроенные. Они являются частью MATLAB, поэтому они очень эффективны, но их вычислительные детали трудно доступны. В то время как другие функции реализованы в М-файлах. Поэтому вы можете легко увидеть их код и, в случае необходимости, даже модифицировать его.
Несколько специальных функций предоставляют значения часто используемых констант, таких как
| pi | 3.14159265… |
| i | мнимая единица  |
| j | то же самое, что и i |
| eps | относительная точность числа с плавающей точкой, 2-52 |
| realmin | наименьшее число с плавающей точкой, 2-1022 |
| realmax | наибольшее число с плавающей точкой, 21023 |
| Inf | бесконечность |
| NaN | не число |
Бесконечность появляется при делении на нуль или при выполнении математического выражения, приводящего к переполнению, т.е. к превышению realmax. Не число (NaN) генерируется при вычислении выражений типа 0-0, которые не имеют определенного математического значения.
Имена функций не являются зарезервированными, поэтому возможно изменять их значения на новые, и далее использовать это значение в последующих вычислениях. Начальное значение может быть восстановлено следующим образом
Встроенные элементарные функции MATLAB включают тригонометрические, гиперболические, экспоненциальные и логарифмические функции, а также функции для работы с комплексными числами и для округления различными способами.
Ниже приведены основные стандартные функции вещественного аргумента.
| Экспоненциальные функции | |
| a^x | Степенная функция |
| x^a | Показательная функция |
| sqrt(x) | Квадратный корень |
| exp(x) | Экспонента |
| log(x) | Натуральный логарифм |
| log10(x) | Десятичный логарифм |
| abs(x) | Модуль |
| fix(x) | Отбрасывание дробной части числа |
| floor(x) | Округление до меньшего целого |
| round(x) | Обычное округление |
| ceil(x) | Округление до большего целого |
| rem(x,y) | Остаток от деления x на y без учёта знака |
| mod(x,y) | Остаток от деления x на y с учётом знака |
| sign(x) | Знак числа |
| factor(x) | Разложение числа x на простые множители |
| Тригонометрические функции | |
| sin(x) | Синус |
| sinh(x) | Синус гиперболический |
| asin(x) | Арксинус |
| asinh(x) | Арксинус гиперболический |
| cos(x) | Косинус |
| cosh(x) | Косинус гиперболический |
| acos(x) | Арккосинус |
| acosh(x) | Арккосинус гиперболический |
| tan(x) | Тангенс |
| tanh(x) | Тангенс гиперболический |
| atan(x) | Арктангенс |
| atanh(x) | Арктангенс гиперболический |
| cot(x) | Котангенс |
| coth(x) | Котангенс гиперболический |
| acot(x) | Арккотангенс |
| acoth(x) | Арккотангенс гиперболический |
Пример. Пусть требуется вычислить значение выражения
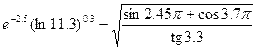
В соответствиями с правилами MATLAB это выражение будет записано следующим образом:
exp(-2.5)*log(11.3)^0.3-sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3));
Статьи к прочтению:
Алгебра 7 класс. 1 сентября. Числовые и алгебраические выражение #1
Похожие статьи:
-
For ( выражение 1 ; выражение 2 ; выражение 3 ) оператор
Лабораторная работа №2 Программирование циклических процессов на языке С++ Цель: Изучение алгоритмов работы циклов и принципы их программирования на…
-
Типы данных и операции в языке си. выражения
Типы данных. Программа на процедурных языках, к которым относится Си, представляет собой описание операций над величинами различных типов. Тип определяет…
