В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений.


Булева, алгебра позволяет не только проводить анализ ЛС, описываемых логическими выражениями или таблицами истинности, но и синтез их из более простых, т.е. решать в комплексе структурно-аналитические вопросы ЛС, Анализ ЛС состоит в установлении ее выходных значений по значениям логических входов, тогда как, соединяя известные ЛС в новую схему на основе описывающего ее логического выражения, производим синтез новых ЛС на основе уже имеющихся.
Элементарные ЛС, используемые при создании средств ЦВТ, называются вентилями (gates); в настоящее время, существует целый ряд базовых вентилей на основе которых строится современная ВТ; некоторые из них рассматриваются ниже. Так как набор {И, .ИЛИ, НЕ} логических операций является универсальным. {функционально полным), т.е. на его основе можно предсхавлять любую логическую функцию» то соответствующий ему набор вентилейтакже будет универсальным:
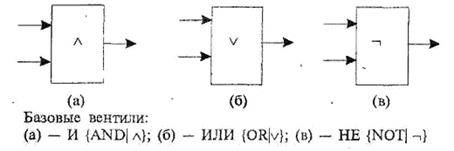
На основе базовых вентилей может быть построена любая ЛС; при этом вентили (а, б) могут иметь любое число входов, определяемое количеством переменных логического выражения, описывающего ЛС. Из математической логики известно» что наряду с (И, ИЛИ, НЕ} функционально полными являются и другие простые наборы базовых операций; (И, НЕ), {ИЛИ, НЕ}, {И-НЕ} (штрих Шеффера), {ИЛИ-НЕ} (стрелка Пирса) и др.
Действительно, например, редуцированная система {И, НЕ} не теряет свойства функциональной полноты, т.к. {Х*У,Х+У,Х’} = {Х*У,(Х’-У’)’Х’}. Например, с учетом сказанного, для логических выражений Y+X-Z и X’-Y+Z предыдущих примеров логические схемы могут иметь достаточно простой вид. Схемы с изображениями элементарных иди базовых ЛС и их связей называются логическими диаграммами (ЛД); если ЛД состоит из вентилей и у нее отсутствуют обратные связи, то соответствующую ей ЛС называют комбинационной.
Ввиду взаимно однозначного соответствия между комбинационными ЛД и- булевыми выражениями, последние используются также для анализа и/или синтеза ЛД/ЛС; наряду с этим, булевы выражения в составе аппарата булевой алгебры широко используются: во многих разделах, современных технических наук. В качестве иллюстрации сказанного приведем ряд простых примеров на представление булевых выражений соответствующими. им логическими схемами, состоящими из базовых вентилей рассмотренных выше типов:
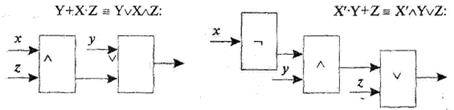
Наряду с рассмотренными тремя базовыми вентилями для синтеза ЛС используется ряд элементарных вентилей; некоторые из них приведем в качестве примера:
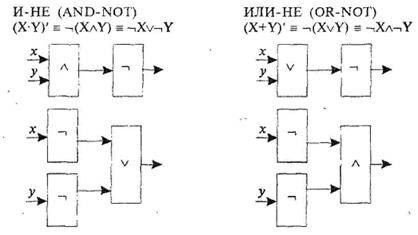
Оба элементарных вентиля являютсяуниверсальными, т.е. на основе каждого из них можно реализовать как ЛС для любой базовой операции {И, ИЛИ, НЕ}.
В качестве примера приведем ДЦ, соответствующую логическому F-выражению» реализованную с использованием только базовых вентилей:
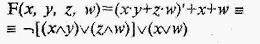
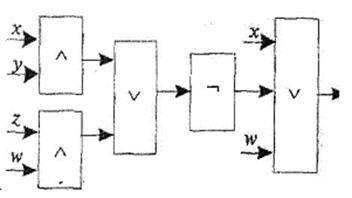
Приведенные примеры представляют простые ЛС, тогда как при разработке реальныхвычислительных узлов и устройств приходится иметь дело с ЛС, описываемыми весьма сложными логическими выражениями.
Здесь приходится решать ряд сложных конструктивных задач: получение ЛС минимальной сложности, ЛС с заданным набором элементарных вентилей, оптимальная топология вентилей и др. Для решения подобных задач используются специальные системы автоматизации проектирования (САПРы), позволяющие эффективно разрабатывать весьма сложные ЛС, содержащие миллионы элементарных вентилей и имеющие сложную топологию. Подробнее подобные ЛС будут рассматриваться ниже. Независимо от реализуемых ими операций логические вентили строятся па основе одних и тех же элементов, главным образом транзисторов — переключателей прохождения тока.
Как уже отмечалось, последовательностная схема отличается от коммутационной наличием памяти; основным ее элементом являются триггер — специальная электронная схема с двумя выходами. Триггерная схема представляет собой специальную ЛС (реализованную на рассмотренных выше логических вентилях) с двумя выходными сигналами {Q,Q’}.
При этом выходной Q-сигнал считается истинным, a Q’-сигнал -инверсным (ложным или дополнительным), Этим сигналам соответствуют два устойчивых состояния триггера. 1 (установка) и 0 (сброс). Под влиянием входного сигнала триггер может скачкообразно (дискретно) переходить из одного устойчивого состояния в другое, при этом дискретно изменяется уровень напряжения его выходного сигнала; высокий (1) и низкий (0) в случае положительной логики.
Схемы триггеров делаться на несколько типов: RS-, Т-, D-, JK-триггер и др. Состояние триггера определяется выходным Q(Q)’-сигyалом, а правила его функционирования задаются таблицами переходов. Схема RS-триггера составляет основу для построения других типов триггеров.
В качестве важных последовательностных схем, выполняемых на одной ИС, можно отметить счетчики, сдвиговые регистры, элементы памяти и др.
Организация машины
Архитектура ЭВМ – это многоуровневая иерархия аппаратно-программных средств, из которых строится ЭВМ. Каждый из уровней допускает многовариантное распределение (построение) и применение. Конкретная реализация уровней определяет особенности структурного построения ЭВМ.
ЭВМ – это устройство, выполненное на электронных приборах, предназначенное для автоматического преобразования информации под управлением программы.
Структурная схема ЭВМ
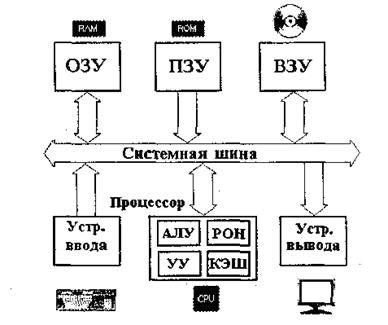
АЛУ – арифметико-логическое устройство
РОН – устройство регистров общего назначения
КЭШ – КЭШ память
УУ – устройство управления
ПЗУ – постоянное запоминающее устройство
ОЗУ – оперативное запоминающее устройство
ВЗУ – внешнее запоминающее устройство
Процессор выполняет логические и арифметические операции, определяет порядок выполнения операций, указывает источники данных и приемники результатов. Процессором управляет программа.
Статьи к прочтению:
Информатика. Выпуск 7. Алгебра логики. Основные законы алгебры логики.
Похожие статьи:
-
Логические элементы эвм. алгебра логики. законы алгебры логики.
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики или, как ее часто называют, булева…
-
Базовыми операциями алгебры логики
операции логического умножения – конъюнкции ( ), логического сложения – дизъюнкции ( ), исключающего или – (A), логического отрицания – инверсии ( )….
