Вероятностный подход к измерения информации.

Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации, полученной при совершении того или иного события можно выразить формулой которую в 1948 году предложил Шеннон.

Формула Шеннона

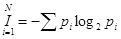
I — количество информации

N – количество возможных событий

pi – вероятности отдельных событий

Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно рассчитать по формуле .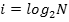

Задания для самостоятельного решения:

1. Сообщение, записанное буквами 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет?

2. Жители планеты Принтер используют алфавит из 256 знаков, а жители планеты Плоттер — из 128 знаков. Для жителей какой планеты сообщение из 10 знаков несет больше информации и на сколько?

3. Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?

4. Цветное растровое графическое изображение, палитра которого включает в себя 65 536 цветов, имеет размер 100х100 точек (пикселей). Какой объем видеопамяти компьютера (в Кбайтах) занимает это изображение в формате BMP?

5. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

6. * Словарный запас некоторого языка составляет 256 слов, каждое из которых состоит точно из 4 букв. Сколько букв в алфавите языка?

7. Сколько информации несет сообщение о том, что было угадано число в диапазоне целых чисел от 684 до 811?

8. В некоторой стране автомобильный номер длиной 7 символов составляется из заглавных букв (всего используется 26 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 20 автомобильных номеров.

9. Каждая клетка поля 8?8 кодируется минимально возможным и одинаковым количеством бит. Решение задачи о прохождении ‘конем’ поля записывается последовательностью кодов посещенных клеток. Каков объем информации после 11 сделанных ходов? (Запись решения начинается с начальной позиции коня).

10. Информационное сообщение объемом 1,5 килобайта содержит 3072 символа. Сколько символов содержит алфавит, с помощью которого было записано это сообщение?

11. Мощность алфавита равна 64. Сколько Кбайт памяти потребуется, чтобы сохранить 128 страниц текста, содержащего в среднем 256 символов на каждой странице?

12. В зоопарке содержится 10 обезьян, причем одна из них выступает в цирке. Обезьяны сидят в двух вольерах, в первом – 8 животных, а во втором — два. Посетитель зоопарка считает, что сообщение «Обезьяна, выступающая в цирке, сидит во втором вольере, содержит 1 бит информации. Прав он или нет? Поясните ответ.

13. В горах рядом с которыми живет племя Тумба-Юмба, есть 4 пещеры. В каждой из них может (а может и не быть) клад. Можно ли закодировать сведения о том, где есть клады, используя 3 бита? 4 бита? 5 бит?

14. Вася задумал число от 1 до 100. Нужно отгадать это число за наименьшее число попыток, задавая Васе вопросы, на которые он отвечает «да» и «нет». За сколько вопросов вы доберетесь до ответа? Какие вопросы вы будете задавать Васе?

Статьи к прочтению:

Вероятностный подход к определению количества информации

Похожие статьи: