Задания для самостоятельного выполнения. вариант 1.даны действительные числа х, у.получить:
Вариант 1.Даны действительные числа х, у.Получить:
а) max (х, у);
б) min(х, у).
Вариант 2.Даны действительные числа а, b, с. Проверить, исполняются ли неравенства a
Вариант 3.Даны действительные числа а, b, с. Удвоить эти гасла, если а³b³с, и заменить их абсолютными значениями, если это не так.
Вариант 4.Даны действительные числа х, у. Вычислить 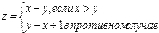 .
.
Вариант 5.Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так.
Вариант 6.Даны два действительных числа. Заменить первое число нулем, если оно меньше или равно второму, и оставить числа без изменения в противном случае.
Вариант 7.Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
Вариант 8.Даны действительные числа х, у (х¹у). Меньшее из этих двух чисел заменить их полусуммой, а большее — их удвоенным произведением.
Вариант 9.Даны три действительные числа. Возвести в квадрат те из них, значения которых неотрицательны.
Вариант 10.Если сумма трех попарно различных действительных чисел х, у, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из х и у полусуммой двух оставшихся значений.
Вариант 11.Даны действительные числа х, у, z. Вычислить:
a) max (х + у + z, хyz);
б) mm2(x + y+ z/2, хyz)+ 1.
Вариант 12.Даны действительные числа х, у. Если х и у отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0.5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях х и у оставить без изменения.
Вариант 13.Даны действительные положительные числа х, у, z. Выяснить, существует ли треугольник с длинами сторон х, у, z. Если треугольник существует, то ответить — является ли он остроугольным.
Вариант 14.Даны действительные числа а, b, с, d, s, t, и (s и t одновременно не равны нулю). Известно, что точки (а,b) и (с, d) не лежат на прямой k, заданной уравнением 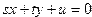 . Прямая k разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (а, b) и (с, d) принадлежат разным полуплоскостям
. Прямая k разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (а, b) и (с, d) принадлежат разным полуплоскостям
Вариант 15.Даны действительные числа а, b, с, d, e, f, g, h. Известно, что точки (е, f) и (g, h) различны. Известно также, что точки (а, b) и (с, d) не лежат на прямой k, проходящей через точки (е, f) и (g, h). Прямая k разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (а, b) и (с, d) принадлежат одной и той же полуплоскости.
Вариант 16.Даны действительные числа х1, х2, х3, у1, у2, у3. Принадлежит ли начало координат треугольнику с вершинами (х1, у1), (х2, у2), (х3, y3)?
Вариант 17.Даны действительные числа х, у, z. Получить:
а) max(х, у, z);
б) min (х, у, z).
Вариант 18.Даны действительные положительные числа а, b, с, d. Выяснить, можно ли прямоугольник со сторонами а, b уместить внутри прямоугольника со сторонами с, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.
Вариант 19.Даны действительные положительные числа а, b, с, х, у. Выяснить, пройдет ли кирпич с ребрами а, b, с в прямоугольное отверстие со сторонами х и у. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.
Вариант 20.Даны действительные положительные числа a, b, c (a¹0). Полностью исследовать биквадратное уравнение 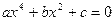 , т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре.
, т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре.
Список основной и дополнительной литературы: 2,3,4,5,7,8,9,12,13,14,15,17,18
Статьи к прочтению:
- Задания для самостоятельного выполнения. вариант 1.создайте web-страницу, в которой должны присутствовать цветной текст, список, рисунок, таблица
- Задания для самостоятельного выполнения. вариант 1. загрузите поисковую систему rambler и выполните поиск рефератов.
Алгебра 8 класс. Квадратный корень
Похожие статьи:
-
Вариант 1. Записать алгоритм вычисления значения y, используя словесную форму описания алгоритма. Y = (2x + 5)(3 ) Вариант 2. Записать алгоритм…
-
Вариант 1. Загрузите поисковую систему Rambler и выполните поиск рефератов. Вариант 2. Найдите сайты о городе Караганда. Вариант 3. Произведите…
