Аргументы тригонометрических функций задаются в радианах. аргумент заключается в скобки}.

Результат выполнения любой операции в выражениях зависит от типов операндов (переменных, констант, функций). Здесь мы рассмотрим только арифметические операции и, соответственно, тип результата может быть целым или вещественным.

Для того чтобы описать последовательность, в которой должны стоять операнды в выражениях и в которой должны расставляться скобки, целесообразно упорядочить операции по уровням.

В таблице 4 указаны арифметические операции и их уровни, а также типы результатов.

Таблица 4. Арифметические операции

Уровень	Операция	Тип операндов	Тип результата	Значение
	***///div mod	Real, realInteger, integerReal, integerReal, realInteger, integerInteger, realInteger, integer Integer, integer	RealIntegerRealRealRealRealInteger Integer	УмножениеУмножениеУмножениеДелениеДелениеДелениеДеление без остаткаОстаток от деления
	+,-+,-+,-	Integer, integerReal, realInteger, real	IntegerRealReal	Сложение ивычитание

Правила приоритетности операций в выражениях:

1.Операции уровня i выполняются до выполнения операций j,ji.

2.Операции одного уровня выполняются поочередно слева направо.

3.Операции, заключенные в круглые скобки, выполняются раньше операций, записанных за скобками.

Эти правила действуют для всех типов выражений (арифметических, логических, строковых).

Последовательность действий, выполняемых при вычислении выражений:

1. Вычисления в круглых скобках.

2. Вычисления значений функций.

3. Унарные операции ( — , not ).

4. Операции типа умножения (*, /, div, mod, and);

5. Операции типа сложения (+, — , or, xor )

6. Операции отношения (=, , , =,

Рассмотрим примеры записи арифметических выражений:

№	Обычная запись	Запись на Паскале

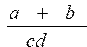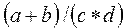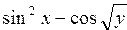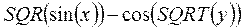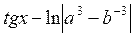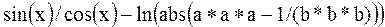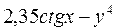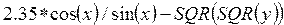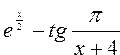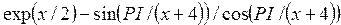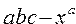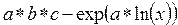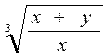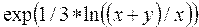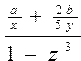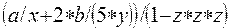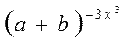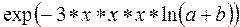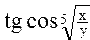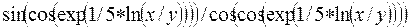Прокомментируем примеры:

Для указания последовательности выполнения действий в числителе и знаменателе появляются круглые скобки (примеры. 1,8).

Из-за отсутствия операции возведения в степень при записи выражений со степенями рекомендуется :

а) возведение в целую положительную степень заменять умножением (примеры 3,8)

б) возведение в целую отрицательную степень заменять делением на произведение сомножителей (пример 3)

в) для четных целых положительных степеней использовать функцию SQR (примеры 2, 4)

г) во всех других случаях возведение в степень вычисляется как экспонента от показателя степени, умноженного на натуральный логарифм степени (примеры 7, 9, 10).

Отсутствие функций tg и ctg приводит к усложнению выражений (примеры 3, 4, 5, 10).

Если аргумент у функции tg или ctg достаточно сложное выражение (примеры 5, 10), рекомендуется ввести новую переменную для обозначения аргумента, например, фрагмент программы для примера 10 можно записать так:

. . . . . . . . . . . .

t : = cos(exp(1/5*ln(x/y))); { аргумент тангенса }

Z : = sin(t)/cos(t); { значение выражения присвоено переменной Z }

. . . . . . . . . . . .

В данном случае действует общая рекомендация при программировании формул об обозначении повторяющихся выражений.

Примеры использования операций mod и div:

Аргументы тригонометрических функций задаются в радианах. аргумент заключается в скобки}.

Статьи к прочтению:

Jillzay ft. 104, Скриптонит — Аргумент (2016)

Похожие статьи: