Классификация моделей надежности по

Термин модель надежности программного обеспечения, как правило, относится к математической модели, построенной для оценки зависимости надежности программного обеспечения от некоторых определенных параметров. Значения таких параметров либо предполагаются известными, либо могут быть измерены в ходе наблюдений или экспериментального исследования процесса функционирования программного обеспечения. Данный термин может быть использован также применительно к математической зависимости между определенными параметрами, которые хотя и имеют отношение к оценке надежности программного обеспечения, но тем не менее не содержат ее характеристик в явном виде. Например, поведение некоторой ветви программы на подмножестве наборов входных данных, с помощью которых эта ветвь контролируется, существенным образом связано с надежностью программы, однако характеристики этого поведения могут быть оценены независимо от оценки самой надежности. Другим таким параметром является частота ошибок, которая позволяет оценить именно качество систем реального времени, функционирующих в непрерывном режиме, и в то же время получать только косвенную информацию относительно надежности программного обеспечения (например, в предположении экспоненциального распределения времени между отказами).

Одним из видов модели надежности программного обеспечения, которая заслуживает особого внимания, является так называемая феноменологическая, или эмпирическая, модель. При разработке моделей такого типа предполагается, что связь между надежностью и другими параметрами является статической. С помощью подобного подхода пытаются количественно оценить те характеристики программного обеспечения, которые свидетельствуют либо о высокой, либо о низкой его надежности. Так, например, параметр сложность программы характеризует степень уменьшения уровня ее надежности, поскольку усложнение программы всегда приводит к нежелательным последствиям, в том числе к неизбежным ошибкам программистов при составлении программ и трудности их обнаружения и устранения. Иначе говоря, при разработке феноменологической модели надежности программного обеспечения стремятся иметь дело с такими параметрами, соответствующее изменение значений которых должно приводить к повышению надежности программного обеспечения.

Рассмотрим классификацию моделей надежности ПС, приведенную на рисунке 3.1. Модели надежности программных средств (МНПС) подразделяются на аналитические и эмпирические. Аналитические модели дают возможность рассчитать количественные показатели надежности, основываясь на данных о поведении программы в процессе тестирования (измеряющие и оценивающие модели). Эмпирические модели базируются на анализе структурных особенностей программ. Они рассматривают зависимость показателей надежности от числа межмодульных связей, количества циклов в модулях, отношения количества прямолинейных участков программы к количеству точек ветвления и т.д. Часто эмпирические модели не дают конечных результатов показателей надежности, однако они включены в классификационную схему, так как развитие этих моделей позволяет выявлять взаимосвязь между сложностью ПС и его надежностью. Эти модели можно использовать на этапе проектирования ПС, когда осуществлена разбивка на модули и известна его структура.

Аналитические модели представлены двумя группами: динамические модели и статические. В динамических МНПС поведение ПС (появление отказов) рассматривается во времени. В статических моделях появление отказов не связывают со временем, а учитывают только зависимость количества ошибок от числа тестовых прогонов (по области ошибок) или зависимость количества ошибок от характеристики входных данных (по области данных).

Для использования динамических моделей необходимо иметь данные о появлении отказов во времени. Если фиксируются интервалы каждого отказа, то получается непрерывная картина появления отказов во времени (группа динамических моделей с непрерывным временем). Может фиксироваться только число отказов за произвольный интервал времени. В этом случае поведение ПС может быть представлено только в дискретных точках (группа динамических моделей с дискретным временем). Рассмотрим основные предпосылки, ограничения и математический аппарат моделей, представляющих каждую группу, выделенную по схеме.

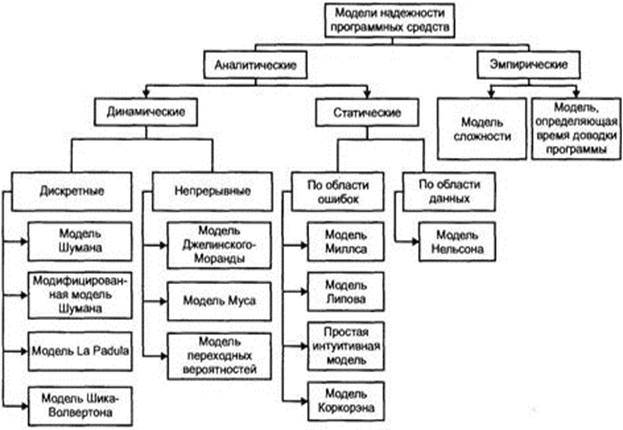
Рисунок 3.1. – Классификационная схема моделей надежности ПС

Аналитическое моделирование надежности ПС включает четыре шага:

1 определение предположений, связанных с процедурой тестирования ПС;

2 разработка или выбор аналитической модели, базирующейся на предположениях о процедуре тестирования;

3 выбор параметров моделей с использованием полученных данных;

4 применение модели – расчет количественных показателей надежности по модели.

Как известно, на данный момент времени разработано большое количество моделей надежности ПС и их модификаций. Каждая из этих моделей определяет функцию надежности, которую можно вычислить при задании ей соответствующих данных, собранных во время функционирования ПС. Основными данными являются отказы и время. Другие дополнительные параметры связаны с типом ПС, условиями среды и данных.

Ввиду большого разнообразия моделей надежности разработано несколько подходов к классификации этих моделей. Такие подходы в целом основываются на истории ошибок в проверяемой и тестируемой ПС на этапах ЖЦ. Одной из классификаций моделей надежности ПО является классификация Хетча. В ней предлагается разделение моделей на прогнозирующие, измерительные и оценочные (рис. 3.2).

Прогнозирующие модели надежности основаны на измерении технических характеристик создаваемой программы: длина, сложность, число циклов и степень их вложенности, количество ошибок на страницу операторов программы и др.

Например, модель Мотли-Брукса основывается на длине и сложности структуры программы (количество ветвей, циклов, вложенность циклов), количестве и типах переменных, а также интерфейсов. В этих моделях длина программы служит для прогнозирования количества ошибок, например, для 100 операторов программы можно смоделировать интенсивность отказов.

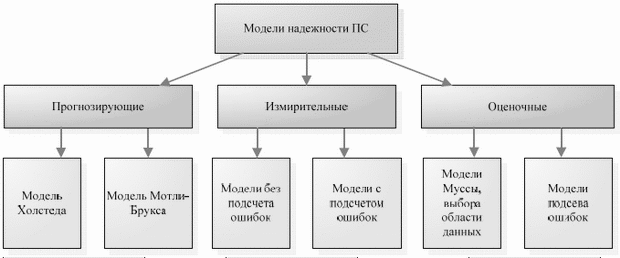
Рис. 3.2. Классификация моделей надежности

Модель Холстеда прогнозирует количество ошибок в программе в зависимости от ее объема и таких данных, как число операций ( ) и операндов ( ), а также их общее число ( ).

Время программирования программы предлагается вычислять по следующей формуле:

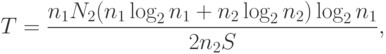
где — число Страуда (Холстед принял равным 18 — число умственных операций в единицу времени).

Объем вычисляется по формуле:

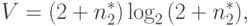
где — максимальное число различных операций.

Измерительные модели предназначены для измерения надежности программного обеспечения, работающего с заданной внешней средой. Они имеют следующие ограничения:

программное обеспечение не модифицируется во время периода измерений свойств надежности;

обнаруженные ошибки не исправляются;

измерение надежности проводится для зафиксированной конфигурации программного обеспечения.

Типичным примером таких моделей являются модели Нельсона и Рамамурти Бастани и др.Модель оценки надежности Нельсона основывается на выполнении k-прогонов программы при тестировании и позволяет определить надежность

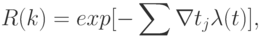
где — время выполнения -прогона, и при она интерпретируется как интенсивность отказов.

В процессе испытаний программы на тестовых прогонах оценка надежности вычисляется по формуле

где — число прогонов программы.

Таким образом, данная модель рассматривает полученные количественные данные о проведенных прогонах.

Оценочные модели основываются на серии тестовых прогонов и проводятся на этапах тестирования ПC. В тестовой среде определяется вероятность отказа программы при ее выполнении или тестировании.

Эти типы моделей могут применяться на этапах ЖЦ. Кроме того, результаты прогнозирующих моделей могут использоваться как входные данные для оценочной модели. Имеются модели (например, модель Муссы), которые можно рассматривать как оценочную и в то же время как измерительную модель.

Другой вид классификации моделей предложил Гоэл, согласно которой модели надежности базируются на отказах и разбиваются на четыре класса моделей:

без подсчета ошибок;

с подсчетом отказов;

с подсевом ошибок;

модели с выбором областей входных значений.

Модели без подсчета ошибок основаны на измерении интервала времени между отказами и позволяют спрогнозировать количество ошибок, оставшихся в программе. После каждого отказа оценивается надежность и определяется среднее время до следующего отказа. К таким моделям относятся модели Джелински и Моранды, Шика Вулвертона и Литвуда-Вералла.

Модели с подсчетом отказов базируются на количестве ошибок, обнаруженных на заданных интервалах времени. Возникновение отказов в зависимости от времени является стохастическим процессом с непрерывной интенсивностью, а количество отказов является случайной величиной. Обнаруженные ошибки, как правило, устраняются и поэтому количество ошибок в единицу времени уменьшается. К этому классу моделей относятся модели Шумана, Шика- Вулвертона, Пуассоновская модель и др.

Модели с подсевом ошибок основаны на количестве устраненных ошибок и подсеве, внесенном в программу искусственных ошибок, тип и количество которых заранее известны. Затем определяется соотношение числа оставшихся прогнозируемых ошибок к числу искусственных ошибок, которое сравнивается с соотношением числа обнаруженных действительных ошибок к числу обнаруженных искусственных ошибок. Результат сравнения используется для оценки надежности и качества программы. При внесении изменений в программу проводится повторное тестирование и оценка надежности. Этот подход к организации тестирования отличается громоздкостью и редко используется из-за дополнительного объема работ, связанных с подбором, выполнением и устранением искусственных ошибок.

Модели с выбором области входных значений основываются на генерации множества тестовых выборок из входного распределения, и оценка надежности проводится по полученным отказам на основе тестовых выборок из входной области. К этому типу моделей относится модель Нельсона и др.

Таким образом, классификация моделей роста надежности относительно процесса выявления отказов, фактически разделена на две группы:

модели, которые рассматривают количество отказов как марковский процесс;

модели, которые рассматривают интенсивность отказов как пуассоновский процесс.

Фактор распределения интенсивности отказов разделяет модели на экспоненциальные, логарифмические, геометрические, байесовские и др.

Статьи к прочтению:

Видеокарты. Кого из производителей выбрать?

Похожие статьи: