Основные вычислительные алгоритмы.

Попытки выработать формальное определение алгоритма привели в 20—30-х годах XX века к возникновению теории алгоритмов. В первой половине XX века разные математики (А.Тьюринг, Э.Пост, А.Н. Колмогоров, А.А. Марков и др.) предложили несколько подходов к формальному определению алгоритма: нормальный алгоритм Маркова, машина Тьюринга, машина Поста и т.д. В дальнейшем было показано, что все эти определения эквивалентны.

Мы рассмотрим формальное определение алгоритма, введенное А.Тьюрингом. Математиком для уточнения понятия алгоритма были предложены абстрактные вычислительные конструкции, которые позже были названы машинами. Машина Тьюринга названа по имени английского математика А/Тьюринга (1912— 1954), который описал ее в 1936 году. Аналогичную концепцию машины ввел позднее, в 1937 году, и независимо от Тьюринга американский математик Э.Пост.

У Алана Тьюринга целью создания такой абстрактной воображаемой машины было получение возможности доказательства существования или несуществование алгоритмов решения различных задач. Руководствуясь этой целью, Тьюринг искал как можно более простую, бедную алгоритмическую схему, лишь бы она была универсальной.

Машина Тьюринга.

Понятие машины Тьюринга. Что же представляет собой машина Тьюринга — машина, при помощи которой оказалось возможным доказать, что для некоторых задач не существует алгоритмического решения?

Машина Тьюринга — это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван машиной по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту; у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.

Прежде чем мы начнем знакомиться с машиной Тьюринга, необходимо сделать два общих замечания относительно объектов, с которыми работают алгоритмы.

Замечание. Одной из причин расплывчатости интуитивного понятия алгоритма является разнообразие объектов, с которыми работают алгоритмы. В вычислительных алгоритмах объектами являются числа. В алгоритме шахматной игры объектами являются фигуры и их позиции на шахматной доске. В алгоритме форматирования текста — слова некоторого языка и правила переноса слов. Однако во всех этих и других случаях можно считать, что алгоритм имеет дело не с объектами реального мира, а с некоторыми изображениями этих объектов. Например, есть алгоритм сложения двух целых чисел. Результатом сложения числовых объектов 26 и 22 будет числовой результат 48. Но мы можем считать, что объектом этого алгоритма является входная последовательность, состоящая из пяти символов: 2 6 + 22, а результатом является последовательность, состоящая из двух символов: 48

При этом мы исходим из того, что имеется набор из 11 различных символов {0, 1,2, 3, 4, 5, 6, 7, 8, 9, +}. Используемые символы будем называть буквами, а их набор — алфавитом. В общем случае буквами могут служить любые символы, требуется только, чтобы они были различны между собой и чтобы их число было конечным.

Определение.Любая конечная последовательность букв из некоторого алфавита называется словомв этом алфавите.

Определение.Количество букв в слове называется длинойслова. Слово, в котором нет букв, называется пустымсловом. Оно часто изображается символом L или а0.

Итак, объекты реального мира можно изображать словами в различных алфавитах. Это позволяет считать, что объектами работы алгоритмов могут быть только слова.

Определение.Слово, к которому применим алгоритм, называется входнымсловом; слово, получаемое в результате работы алгоритма, называется выходным.Совокупность слов, к которым применим алгоритм, называется областью применимости алгоритма.

К сожалению, нельзя доказать, что все возможные объекты можно описать словами, так так само понятие объекта не было формально (то есть строго) определено. Но можно проверить, что для любого наугад взятого алгоритма, работающего не над словами, его объекты можно выразить так, что они становятся словами, а суть алгоритма от этого не меняется.

Замечание 2. Любой алфавит можно заменить другим. Такая замена называется кодировкой. Например, каждой букве из первого алфавита ставится в соответствие код, представляющий собой слово во втором алфавите. В качестве второго алфавита достаточно иметь алфавит из двух букв, так как любое слово из любого алфавита можно закодировать в двухбуквенном алфавите с гарантией однозначного восстановления закодированных слов. Следовательно, любой алгоритм можно свести к алгоритму над словами в алфавите {0, 1}, а перед применением алгоритма входное слово следует закодировать, после применения алгоритма выходное слово раскодировать.

Выводы

Можно считать, что алгоритмы работают со словами.

Мы формально описываем объекты-слова, над которыми работают алгоритмы, в некотором алфавите.

Далее для уточнения понятия алгоритма следует формально описать действия над объектами-словами и порядок выполнения этих действий. В качестве такой формальной схемы мы и рассмотрим машину Тьюринга.

В каждой машине Тьюринга есть две части:

неограниченная в обе стороны лента, разделенная на ячейки;

автомат (головка для считывания/записи, управляемая программой).

С каждой машиной Тьюринга связаны два конечных алфавита: алфавит входных символов А = {а0, а1,…,аm} и алфавит состояний Q = {q0, q1,…, qp} . (С разными машинами Тьюринга могут быть связаны разные алфавиты А и Q) Состояние q0 называется пассивным. Считается, что если машина попала в это состояние, то она закончила свою работу. Состояние q1 называется начальным. Находясь в этом состоянии, машина начинает свою работу.

Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит пустая буква а0 — признак того, что ячейка пустая).

Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.

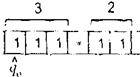
Автомат каждый раз видит только одну ячейку. В зависимости от того, какую букву а, он видит, а также в зависимости от своего состояния qj, автомат может выполнять следующие действия:

записать новую букву в обозреваемую ячейку;

выполнить сдвиг по ленте на одну ячейку вправо/ влево или остаться неподвижным;

перейти в новое состояние.

То есть у машины Тьюринга есть три вида операций. Каждый раз для очередной пары (ai, qj) машина Тьюринга может выполнить определенную команду в соответствии с программой.

Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.

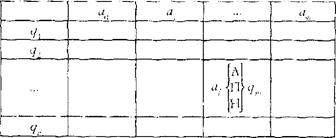
Клетка (ai, qj) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: куда передвинуть головку чтения/записи, какой символ записать в текущую ячейку, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: Л (влево), П (вправо) или Н (неподвижен).

После выполнения автоматом очередной команды он переходит в состояние qm (которое может в частном случае совпадать с прежним состоянием qj ). Следующую команду нужно искать в m-й строке таблицы на пересечении со столбцом al (букву аl автомат видит после сдвига),

Если следить только за лентой, не обращая внимания на автомат, то мы увидим, что в результате выполнения каждой команды изменяются слова: какие-то буквы стираются и вместо них остаются пустые ячейки, в каких-то пустых ячейках появляются новые буквы.

Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в состоянии qj. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q0. Эта клетка называется клеткой останова. Дойдя до такой клетки, машина Тьюринга останавливается.

Если клеток останова в программе нет, то считается, что машина Тьюринга неприменима к данному входному слову. Если клетки останова в программе есть, но машина на них не попадает, также считается, что машина Тьюринга неприменима к данному входному слову. Машина Тьюринга применима к входному слову только в том случае, если, начав работу над этим входным словом, она рано или поздно дойдет до клетки останова.

Прослеживая работу машины Тьюринга, мы можем узнать, что она применима к данному слову. Но если она неприменима к данному слову, то такое прослеживание ничего не даст, так как в любой момент времени мы можем надеяться дойти до клетки останова.

Таким образом, неприменимость не может быть выяснена прямым способом; в ней можно убедиться только путем косвенных рассуждений. Например, если в программе нет клетки останова, то данная машина Тьюринга неприменима ни к одному слову. Или, например, в программе некой машины Тьюринга с алфавитом {0, 1} есть клетка останова, но первая строка программы (таблицы) имеет следующий вид:

Тогда, что бы автомат ни увидел на ленте, он ничего не меняет и сдвигается на шаг вправо, оставаясь всегда в состоянии q1. А поскольку лента бесконечна, он никогда не остановится.

Статьи к прочтению:

[Коллоквиум]: Как создавать нейросети на основе классических вычислительных алгоритмов

Похожие статьи: