Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц

      Комментарии к записи Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц отключены

Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Перевод правильных десятичных дробей в любую другую позиционную систему счисления

При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.

Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.

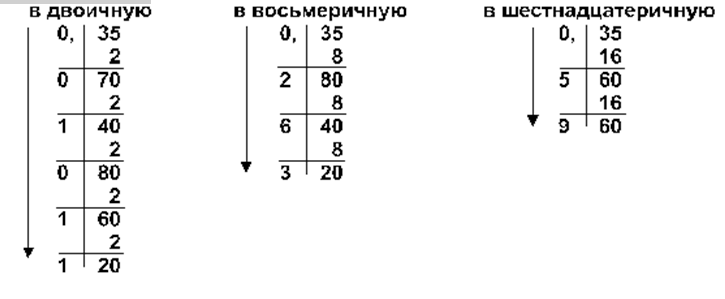
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ:

0,35(10)=0,01011(2)=0,263(8)=0,59(16)

Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Все двоичные числа записаны в четырёхзначном виде (там, где знаков меньше четырёх, слева добавлены нули). Проделаем следующее: каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четвёрку двоичных знаков. Т.е., перекодируем число 15FC по таблице в двоичную форму. Получается:
0001 0101 1111 1100.

Если отбросить нули справа (в любой системе счисления они не влияют на значение целого числа), то получим искомое двоичное число.

десятичная восьмеричная двоичная шестнадцатеричная двоичная
— —
— —
— — — А(10)
— — — B(11)
— — — C(12)
— — — D(13)
— — — E(14)
— — — F(15)

Перевод в двоично-десятичную систему (ДДК — двоично-десятичное кодирование)

Для перевода из десятичной системы в ДДК, каждая цифра десятичной системы записывается в виде четырех разрядов двоичной системы.

Пример: 351(10)=0011 0101 0001(2-10)

Преобразуем теперь двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит прямо преобразуется в ее десятичный эквивалент, и тогда получаем 1000 0000 0111 0010ДДК=807210.

десятичное ДДК=(2-10)

Статьи к прочтению:

Таблица триад и тетрад. Системы счисления.


Похожие статьи: