Решение задач с использованием функций

Цель работы.

Изучить и освоить методы составления функций и обращения к ним при решении задач на языке С++.

Подготовка к работе.

Изучить правила составления функций. Необходимо знать основные способы организации взаимодействия основной программы (функции main) и функции, определяемой пользователем [лекция 13].

Теоретическая часть.

Функция в C++ это логически самостоятельная именованная часть программы, состоящая из нуля (в противном случае) или более операторов, объединённых в исполнимый модуль для решения определённой задачи.

Функции нужны для упрощения структуры программы. Разбив задачу на подзадачи и оформив каждую из них в виде функций, мы делаем программу более гибкой и компактной. Передача в функцию различных аргументов позволяет, записав ее один раз, использовать многократно для разных данных.

Неграмотно написанная функция наряду с аргументами использует и глобальные переменные, которые доступны из любого блока текущего файла.

Для использования функции требуется знать только ее интерфейс (правила обращения и общения). Интерфейс функции определяется ее заголовком, потому что в нем указывается все, что необходимо для ее вызова: имя функции, тип результата, который она возвращает, а также сколько аргументов и какого типа ей нужно передать.

Все, что передается в функцию и обратно, должно отражаться в заголовке (объявлении, прототипе). Это не требование синтаксиса, а хорошего стиля.

Формат простейшего заголовка функции:

тип имя ( [ список_параметров ] );

где спецификация тип- задаёт тип возвращаемого функцией значения. Если указание типа отсутствует, то считается, что функция возвращает значение int. Если вместо типа стоит ключевое слово void, то считается, что функция не возвращает в вызывающую программу никакого значения. Особый случай, когда используется тип void* — родовой указатель. В этом случае результат работы функции есть указатель.

Имя — идентификатор произвольного вида, являющийся указателем на функцию, значение которого равно адресу точки входа в функцию.

Список_параметров — это последовательность объявлений формальных параметров, разделённых запятыми. В C++ допускается использование функций без формальных параметров. Такой случай возникает, когда в функцию не передаются никакие аргументы. Тогда, поле формальных параметров может быть пустым, или содержать ключевое слово Void. Допускается определение формальных параметров по умолчанию (см. ниже.).

При вызове функции с формальными параметрами компилятор вставляет в код программы последовательность машинных команд, обеспечивающих запись, перечисленных в списке аргументов в стек.

Определение функции, кроме заголовка, включает ее тело, т.е. те операторы, которые выполняются при вызове функции.

В тексте программы может содержаться произвольное количество объявлений одной и той же функции и только одно определение. Тело функции представляет собой блок, заключенный в фигурные скобки. Для возврата результата, вычисленного функцией, служит оператор return.

Оператор return — необязательный оператор, обеспечивающий выход из функции. Если оператор return используется совместно с выражением, то выход из функции сопровождается передачей вычисленного значения в точку вызова. Тип результата должен совпадать или быть совместимым с типом функции. При отсутствии оператора return выход из функции происходит после выполнения последнего оператора в теле функции.

Для вызова функции надо указать ее имя, а также передать ей набор аргументов в соответствии с указанным в ее заголовке списком. Соответствие должно соблюдаться строго. В определении, в объявлении и при вызове одной и той же функции типы и порядок следования параметров должны совпадать. Для имен параметров никакого соответствия не требуется.

Вызов функции возвращающей значение определенного типа (не тип void), может быть записан в любом месте, где по синтаксису допустимо выражение – в правой части оператора присваивания, в составе выражения, в цепочке вывода и т.д

В C++ определено несколько способов передачи параметров функции и получения результатов вычисления функции, вызывающей средой. Существует четыре специфики передачи параметров функции:

— вызов функции с передачей значений;

— вызов функции с передачей адресов переменных;

— вызов функции с использованием механизма ссылок при передаче параметров;

— посредством глобальных параметров.

Вызов функции с передачей значений. Этот способ передачи параметров обеспечивает передачу копий переменных в стек, организуемый при активизации функции. При этом обеспечивается защита самих переменных от их изменения в функции.

В качестве примера рассмотрим простейшую программу рассчета суммы пар чисел. Головная программа (функция-main) дважды вызывает функцию sum(), которая возвращает ей результат суммирования двух целых чисел (тип int). Результаты выдаются на экран. Определение переменных, ввод их значений и выдача результатов суммирования на экран выполняются в головной функции. Нарисуем блок-схему алгоритма программы (см. рис.4). Как видно из рисунка для каждой функции разрабатывается своя блок-схема алгоритма и каждый вызов функции оформляется отдельным блоком «типовой процесс» (прямоугольник с двойной вертикальной стороной). Обратите внимание также на блоки «начало процесса» и «конец процесса», которые у вызываемой (функция sum()) и вызывающей (функция main()) функций несколько отличаются. Программный код будет выглядеть так:

#include

int sum(int,int); // объявление функции, т.к. определение

// следует после вызова функции

void main(void)

{int a,b,c,p; // определение используемых переменных

cinabp; // ввод значений переменных a, b, p

c=sum(a,b); // вызов функции sum() с передачей

// параметров значений

cout

b=sum(p,c); // повторный вызов ф-ции sum()

cout

}

// определение функции

int sum(int d, int l) // заголовок

{ // тело функции

int f;

f=d+l; // суммирование переданных значений

return f;// результат передаётся в точку вызова

}

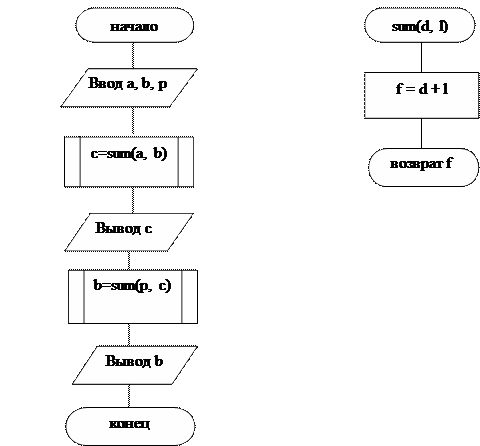
Рис.4. Блок-схемы вызывающей программы и вызываемой функции sum

Вызов функции с передачей адресов. Этот способ передачи параметров обеспечивает передачу в стек адресов передаваемых данных, что позволяет функции работать непосредственно с данными.

#include

sum(int,int,int*); // объявление функции

void main( )

{int a,b,c=0;

cinab;

sum(a,b,c); // вызов функции

cout

}

void sum(intd,intl,int*f) // определение функции

{

*f=d+l // f – указатель на c

}

Вызов функций с использованием механизма ссылок. Этот способ обеспечивает доступ к передаваемым параметрам посредством определения их альтернативного имени. Например:

#include

sum(int,int,int);

void main( )

{

int a,b,c=0;

cinab;

sum(a,b,c);

cout

}

//void

sum(int d,int l,int f)

{

f=d+l; // f- ссылка на c

}

Вызов функции с передачей данных посредством глобальных параметров. Этот способ передачи исходных данных в вызываемую функцию и возвращения результата вычислений путём использования глобальных параметров. Например:

#include

int a,b,c;

sum(); // объявление функции

main()

{

cinab;

sum(); //вызов функции

cout

}

sum() // определение функции

{c=a+b; //a,b,c- глобальные переменные

}

Вызов функции с передачей аргументов по умолчанию.В языке С++ начиная с версии 3.11 и выше, определена возможность передачи значений аргументов функции по умолчанию. Этот способ передачи значений параметров используется в том случае, когда необходимо обеспечить передачу только части значений параметров, а не всех.

Объявление значений функции по умолчанию производится путём указания значений аргументов в прототипе функции посредством оператора присваивания.

#include

float ur(float x,float a=0.,float b=0.,float c=0.);

int main()

{float a=1.,b=2.,c=3.,x=0.5,y;

y=ur(x,a,b,c);

cout

y=ur(x,a,b);

cout

y=ur(x);

cout

cina;

}

float ur(float x,float a,float b,float c)

{

return a*x*x+b*x+c;}

На экране дисплея мы получим следующие результаты работы вышеприведенной программы.

Введены все аргументы

4.25

введены x,a и b

1.25

введен x

В языке C++ допустима рекурсия. Рекурсия это способ организации вычислительного процесса, при котором процедура или функция может обращаться сама к себе. Покажем рекурсивную реализацию метода быстрой сортировки. В методе используется процедура половинного разделения, применяемая на 1-ом шаге ко всему массиву, а на следующих шагах – к его фрагменту. На каждом шаге образуются две половинки текущего фрагмента, к которым снова применяется процедура разделения. Если массив сортируется по возрастанию, то в левую половинку записываются меньшие значения, а в правую – большие (если по убыванию, то наоборот).

Одну из возможных версий программы покажем на примере:

#include

void quicksort(float* arr, int left,int right);

void main()

{const int n = 10;

float ar[n];

int i, l, r;

//cputs(«введите данные о значениях исходного массива»);

for(i=0; i

cout

cinar[i];

}

l = 0; r = n – 1; //левая и правая границы начального фрагмента

quicksort(ar, l, n); // вызов функции

for(i=0; i

printf(“ar[ %d ]= %d \n”, i, ar[i]); // cout

}

void quicksort(float * arr, int left, int right)

{int i = left, j = right; //левая и правая границы фрагмента

float middle = arr[(left + right) / 2];

float temp;

while (ij) {

while (arr[i]middle) i++;

while (middlearr[j]) j—;

if (i

temp = arr[i];

arr[i] = arr[j];

arr[j] = temp;

i++;

j—;

}

if(iright)quicksort(arr, i, right); /* вызов функции для

сортировки правой половины фрагмента массива */

if(leftj)quicksort(arr, left, j); /* для сортировки левой

половины фрагмента */

}

Процедура разделения реализована в виде рекурсивно вызываемой функции quicksort(), в теле которой есть два обращения к самой себе: для сортировки левой половинки теккущего фрагмента и сортроки его правой половинки.

Однако, у рекурсии есть недостатки:

— такую программу труднее отлаживать, поскольку требуется контролировать глубину рекурсивного обращения;

— при большой глубине стек может переполниться;

— использование рекурсии повышает накладные расходы (в данном случае в стеке сохраняются не два числа, представляющие собой границы фрагмента, а гораздо больше, не говоря уже о затратах, связанных с вызовом функции).

Поэтому рекурсию следует применять с осторожностью.

Задание.

Для выданного преподавателем варианта задачи написать и отладить программу на языке С++, которая содержит функцию (или несколько функций) .

Способ передачи параметров при обращении к функции обоснуйте.

5. Требования к отчету по лабораторной работе:

Отчет должен содержать:

1) распечатку или текст программы с комментариями;

2) блок-схемы алгоритмов главного модуля и функций пользователя;

3) результаты работы программы.

6. Варианты индивидуальных заданий .

1.Вычислить

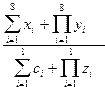
2. Вычислить

Y= 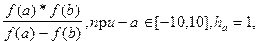b 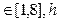b=0.5.

f(х) = 5×3 + sin2x,

3. Вычислить

Z= 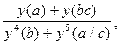при a=2.5 ,b=4.8 ,c=4.2

если y(x) = x5 * cos2(1/x) .

4. Вычислить

F(x,y)= 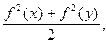при x 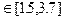; hx=0.25; y 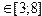; hy=1.25;

если f(z) = 2 * 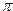*z.

5. Вычислить

A= 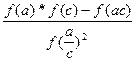, при a=5.62 , c , hc=0.5 ,

если f(x)=sin x2-5x+20lg(x).

6. Вычислить

B= , при a 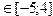, ha=1, b=2.8 , c=3.2 ,

если f(x)=x3+3×2+arctg x .

7. Вычислить

Zij=f(xi,yj) , при 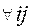, x=(0.34;0.56;1;3) ,y=(0.76;0.12;2;4)

если f(x,y)=cos(x2+1)sin2y.

8. Вычислить

yi=f(ci)-f(b)-f(a) , при a=6.1; b=4.3; c=(6;7.6;9.5)

если f(x)= .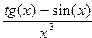

9. Вычислить

Zij=f(xi,yj) , при 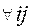, x=(0.1;0.12;4) , y=(3.2;8.39; 3),

если f(x,y)=sin x2/3*e-y2 .

10. Вычислить

y =f(x1)+f(x2)*f(x3) , при x1=0.32; x2=8.5; x3=2; ,

если f(x)= .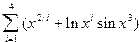

11. Вычислить

y =f(x1)*f(x2)/f(x3) , при x1=a2+5; x2=3.14; x3=0; ,

если f(x)= .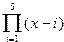

12. Вычислить

y =f(x1)+f(x2)-f(x3) , при x1=ln(2.3); x2=cos(1.2); x3=1; ,

если f(x)= .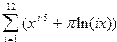

13. Вычислить

y = 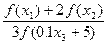, при x1=2.6; x2=8.7; x3=0.1; ,

где f(x)=x3/2+6×2+tg(x) .

14. Вычислить наименьшие значения каждой из трёх функций

x=cos t2; y=cos t3; z=cos t4;

если t 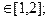ht=0.1 .

15. Вычислить

y=(f(2×1)-f(x1*x2))/f(x3), при x1=3.3; x2=4.2; x3=5.6; ,

если f(x)=sin(x)/x +x sin(1/x) .

16. Вычислить значения индексов, соответствующих наибольшему элементу каждой из трёх произвольно заданных матриц A[5][5], B[5][5], C[5][5].

17. Вычислить номер i , для которого каждая из функций x=t/ln(t) , y=cos(t2/3), определённая на дискретном множестве ti (t 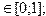ht=0.1), принимает наименьшее значение.

18. Вычислить номера i , для каждого из которых функции

fj(x,cj)= e-(x-cj) *cos(x) ,

определённые на дискретном множестве ti ( c=(0.1; 0.3; 0.5; 0.9) , x 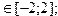hx=0.1 ),

принимают наибольшие значения.

19. Вычислить наибольшие значения каждой из трёх функций

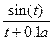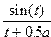x = , y = , z = ,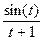

на дискретном множестве ti (t 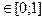; ht=0.1; a=4).

20. Вычислить

yi=f(x1/5)*f(x2)-f(ci) , x1=0.25; x2=6.5; c=(6;7.6;9.5),

если f(x)= .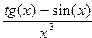

21.Определить средние значения для элементов находящихся ниже побочной диагонали

матриц F[5][5], G[5][5], S[5][5].

22. Вычислить

y= 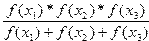, при x1=2.6; x2=8.7; x3=0.1; ,

где f(x)=6×2+tg(x) .

23.Вычислить

Zij=f(xi,yj) , при 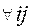, x=(0.1;0.5;4) , y=(2.2;8.39; 3),

если f(x,y)=tg x2*e-y2 .

24. Вычислить

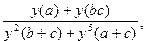
если y(x)=x2*tg2(1/x), при a=1.5 ,b=3.5 ,c=2.2 .

25. Вычислить

y =f(x1)+f(x2)/f(x3) , при x1=0.25; x2=5.5; x3=2; ,

если f(x)= .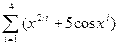

26. Вычислить

R = f(n*m,k)+ f2(k,n)-f3(m,n), при k= 3.6; m= 2.2; n = 5

если f(a,b)=sin2(lg(ab))+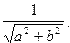

27. Вычислить сумму элементов побочной диагонали каждой из матриц А[3][3], B[5][5], D[6][6].

28. Вычислить

D = P3(a[i][j], b[j][i]) – Р(i, j), где i 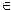[0; 4], j 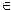[0; 5],

если P (k, h) = 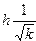— 1.

29. Вычислить сумму отрицательных элементов каждой из матриц А[3][3], B[4][3], D[5][4].

30. Вычислить минимальное из положительных элементов каждого из массивов N(11) и M(11)

Контрольные вопросы.

1.Основные правила составления функций.

2.Объяснить назначение оператора return.

3.Какие типы функций поддерживаются языком C++?

4.Место расположения функции по отношению к основной программе.

5.Какие типы формальных и фактических параметров поддерживаются языком C++?

Список рекомендуемой литературы.

Основная:

1. Канцедал С. А. Алгоритмизация и программирование [Текст] : учебное пособие / С.А. Канцедал. — М. : ИНФРА-М, 2008 ; М. : Форум, 2008. — 352 с. : ил. — ISBN 978-5-8199-0355-1 : 157.41

2. Колдаев В. Д. Основы алгоритмизации и программирования [Text] : учебное пособие / В.Д.Колдаев ; Под. ред. проф. Л.Г.Гагариной. — М. : ИД ФОРУМ : ИНФРА-М, 2009. — 416 с. : ил. — ISBN 978-5-16-002690-9 : 116.05

3. Павловская Т. А. С/С++ Программирование на языке высокого уровня [Text] / Т.А.Павловская. — СПб. : Питер, 2009. — 461 с. : ил. — ISBN 978-5-94723-568-5 : 176.99

5. Павловская, Т. А. С/С++ Структурное программирование [Text] : практикум / Т.А.Павловская, Ю.А.Щупак. — СПб. : Питер, 2007

6. Пантелеев А. В. Методы оптимизации в примерах и задачах [Text] : учебное пособие / А.В. Пантелеев, Т.А. Летова. — 3-е изд., стер. — М. : Высшая школа, 2008. — 544 с. : ил. — ISBN 978-5-06-004137-8 : 633.93

7. Культин, Н. С/С++ в задачах и примерах [Text] / Н. Культин. — 2-е изд., перераб. и доп. — СПб. : БХВ — Петербург, 2011. — 368 с. : ил. эл. опт. диск (CD-ROM). — ISBN 978-5-94157-406-3 : 233.26

8. Козырь О.Ф. Программирование и основы алгоритмизации. Методические указания к выполнению лабораторных работ.(очная и заочная формы обучения) — Старый Оскол: Изд-во СОФ МИСиС, 2012.

9. Бритик В.И., Козырь О.Ф. Программирование и основы алгоритмизации. Основы программирования. Основы программирования и алгоритмизации. Методические указания к выполнению домашних и курсовых работ (очная, очно-заочная и заочная формы обучения) — Старый Оскол: Изд-во СОФ МИСиС, 2008 – 60 с.

10. Козырь О.Ф. Программирование и основы алгоритмизации. Методическое пособие (очная и заочная формы обучения) — Старый Оскол: Изд-во СОФ МИСиС, 2008.

Дополнительная:

1. Агальцов В. П. Математические методы в программировании [Текст] : учебник / В.П.Агальцов. — 2-е изд, перераб. и доп. — М. : ИД ФОРУМ, 2010. — 240 с. : ил. — ISBN978-5-8199-0410-7 : 175.01

2. Чиртик, А. А. Программирование на C++. Трюки и эффекты [Text] / А.А.Чиртик. — CПб : Питер, 2010. — 352 с. : ил + 1 эл. опт. диск (CD-ROM). — ISBN 978-5-49807-102-2 : 319.99

3. Крячков А. В. Программирование на С и С++. Практикум [Text] : учебное пособие для вузов / А.В. Крячков, И.В. Сухинина, В.К. Томшин ; под ред. В.К. Томшина. — 2-е изд., испр. — М. : Горячая линия-Телеком, 2000. — 344 с. : ил. — ISBN 5-93517-014-0 : 58.50 , 69.30

Статьи к прочтению:

Практикум 7: Решение краевых задач с использованием функции Грина

Похожие статьи: