Тема.4. векторные и матричные операции
Цели работы:
- Изучить работу с векторами и матрицами.
Место проведения: аудитория ___.
Ход работы.
При определении векторов и матриц действуют те же правила присваивания и вывода, что и для обычных переменных. Так, для определения вектора A (он изображается в виде вектора-столбца) необходимо набрать А:=, после чего следует на панели Матрица нажать на символическое изображение матрицы. Появится окно диалога, в котором предлагается указать число столбцов и строк (для вектора число столбцов равно единице, а число строк равно размерности вектора).
Для работы с матрицами и векторами математический процессор MathCad имеет ряд операторов и функций. Приведем правила для их использования:
Оператор Ввод Назначение оператора

Пример выполнения задания:
Задание:
| Координатыточек | Матрица |
| A=(-1, 2, 9)B=(7, -2, -4)C=(-1, -5, -1)D=(-3, -1, 4) | 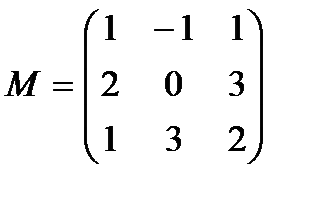 |
Для выполнения задания 1 используем известную
1. формулу из курса линейной алгебры, которая гласит, что координаты вектора численно равны разности координат точек конца и начала вектора:
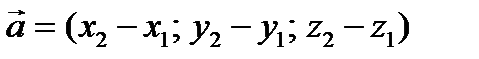 . (1)
. (1)
Для этого в MathCAD точки A, B, C и D набираются в следующем виде:

Для чего открываем панель инструментов «Математика» (View\Toolbars\Math) и нажимаем на ней кнопку «Матрицы» ([MMM])
Далее задаем параметр i, меняющийся от 0 до 2 (для чего на панели «Матрица» есть кнопка вида “m..n”).
Примечание. Отметим, что в пакете MathCAD нумерация компонент векторов и элементов матриц начинается с 0:

Для нахождения координат наших векторов используем формулу (1), которая в MathCAD имеет вид:

Для просмотра координат векторов достаточно набрать «a=» и «b=». В данной задаче

Рекомендация: предлагаем читателю самостоятельно вычислить в MathCAD длину полученных векторов.
2. Вычислим скалярное и векторное произведение полученных векторов.
Примечание. Обращаем внимание на то, что вычисление скалярного произведения в MathCAD осуществляется согласно правилу умножения матриц.
В связи с этим вектора следует задавать следующим образом:

E egSykHuqKyXbEzGNhDY//QEZTp202HJgYudjA5otdmMLJZbr0KIVWqgtLBu2kJtMKrH30EmLBlsE eCByq9vYAstjVVoPEcerNFu84OjY/lkL21LbHTRbtNhC7UBqsIVi1iPEFp6Hq01ygS3PrzbIAuR9 uMlznFiGHZotNFu89KBpF7ZQG1ZOhS3gNJ04eC7U4eqQPD/Z3izDdfMo/8U/AAAA//8DAFBLAwQU AAYACAAAACEAy1PwE+EAAAAMAQAADwAAAGRycy9kb3ducmV2LnhtbEyPXUvDMBSG7wX/QziCdy6N s2GrTccY6tUQ3ATZXdactWVNUpqs7f69Z1d6d17Ow/uRrybbsgH70HinQMwSYOhKbxpXKfjevz8t gIWondGtd6jgigFWxf1drjPjR/eFwy5WjExcyLSCOsYu4zyUNVodZr5DR7+T762OJPuKm16PZG5b /pwkklvdOEqodYebGsvz7mIVfIx6XM/F27A9nzbXwz79/NkKVOrxYVq/Aos4xT8YbvWpOhTU6egv zgTWkhaLJaEK5pI23QCRyhTYkS75kkjgRc7/jyh+AQAA//8DAFBLAQItABQABgAIAAAAIQC2gziS /gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgA AAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgA AAAhAL/iwKFQBgAAEkAAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAG AAgAAAAhAMtT8BPhAAAADAEAAA8AAAAAAAAAAAAAAAAAqggAAGRycy9kb3ducmV2LnhtbFBLBQYA AAAABAAEAPMAAAC4CQAAAAA=
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Примечание. Верхний индекс Т у вектора а означает операцию транспонирования и являетсярезультатом работы кнопки MT на панели «Матрица».
Вычислим скалярное произведение:

Проверим результат, воспользовавшись определением скалярного произведения:

или в виде

Примечание. Если вектор задан в строчку, то MathCAD воспринимает его не как вектор, а как матрицу с одной строкой и n столбцами. Для набора нижнего индекса можно нажимать на клавиатуре кнопку [.
Для вычисления векторного произведения вектора следует задавать в виде столбцов.
В качестве примера продемонстрируем проверку антикоммутативности векторного произведения
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |

3. Рассмотрим произведение матрицы на вектор. Матрица задается с помощью встроенных функций пользователя, а произведение ее на вектор в MathCAD имеет вид:

Умножение вектора на матрицу осуществляется следующим образом:

4. Вычисление определителя матрицы выполняется с помощью встроенной символьной операции  .
.
Задание
Даны два вектора, две матрицы и число: Z = 0.754,
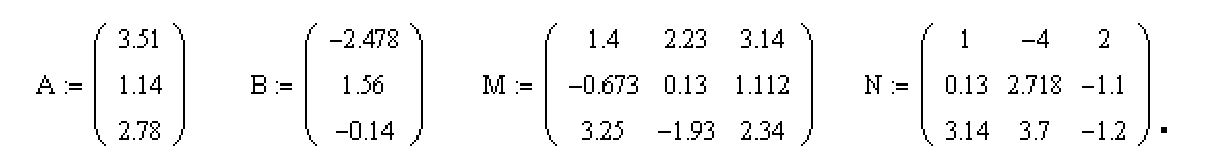
Вычислить:
1. Сумму А+В, разность А-В.
2. Произведение Z*А, сумму (1-Z)*A+Z*B.
3. Скалярное и векторное произведения векторов А и В.
4. Модули векторов А и В.
5. Произведение вектора на матрицу A*M и матрицы на вектор M*A.
6. Определители матриц M и N.
7. Скалярное произведение вектора А и второго столбца M матрицы M.
8. Найти двумя способами решение системы линейных уравнений М?Т =
А, где Т — вектор неизвестных.
Контрольные вопросы
1. Назовите способы выполнения символьных операций в MathCAD.
2. Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме?
3. Перечислите символьные операции с выделенными выражениями.
4.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Перечислите символьные операции с выделенными переменными.
5. Перечислите символьные операции с выделенными матрицами.
6. Перечислите символьные операции преобразования.
7. Какие параметры определяет стиль представления результатов вычислений и где он задается?
8. В каких случаях результат символьных преобразований помещается в буфер обмена?
9. Каким образом можно вычислить предел в MathCAD?
Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб. : БХВ-Петербург, 2006. -336 с. : ил.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.
4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с.
5. Ушаков А. Н. , Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. — №—с.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| Разраб. |
| Провер. |
| Скачкова Л.П. |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Лит. |
| Листов |
| КФ ГОУ ОГУ |
ЛАБОРАТОРНО – ПРАКТИЧЕСКАЯ РАБОТА 5.
Статьи к прочтению:
Лекция 9: Векторная алгебра
Похожие статьи:
-
Тема: файловая структура ос. операции с файлами
Тема: Файловая структура ОС Задание 1 Тема: Файловая структура ОС. Операции с файлами В некоторой папке хранится список файлов, первоначально…
-
Тема: системы счисления. операции над двоичными кодами. перевод из одной системы счисления в другую.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РК Казахский национальный технический университет имени К.И.САТПАЕВА Кафедра информатики САМОСТОЯТЕЛЬНАЯ РАБОТА № 1, 2…
