Вычисление суммы бесконечного ряда с заданной точностью.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
СТАРООСКОЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ им. А.А. Угарова
(ФИЛИАЛ) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
«МИСиС»
о
Козырь О.Ф.
ПРОГРАММИРОВАНИЕ И АЛГОРИТМИЗАЦИЯ
Методическое пособие к выполнению
Лабораторных работ
Для студентов специальностей
140604 – Электропривод и автоматика промышленных установок и технологических комплексов
220301 – Автоматизация технологических процессов и производств
( все формы обучения)
Квалификация (степень) выпускника
Бакалавр
Одобрено редакционно-издательским советом института
Старый Оскол
Год
УДК 004
ББК 32.97
К 593
Рецензент:
Козырь О.Ф. Алгоритмизация организационных задач систем управления. Методические указания к выполнению лабораторных работ и домашних заданий. Старый Оскол. СТИ МИСиС, 2013г, — 72с.
Методическое пособие по курсу «Программирование и алгоритмизация».
© Козырь О.Ф.
© СТИ МИСиС
Содержание.
Введение…………………………………………………………………….
Лабораторная работа №1. Вычисление суммы бесконечного
ряда с заданной точностью…………………………………………………
Лабораторная работа №2. Решение задач с использованием массивов…
Лабораторная работа №3. Решение задач с использованием структур….
Лабораторная работа №4. Решение задач с использованием функций….
Список рекомендуемой литературы………………………………………..
Введение
Настоящий цикл лабораторных работ разработан по дисциплине Программирование и алгоритмизация для студентов очной, очно-заочной и заочной форм обучения специальностей Автоматизация технологических процессов и производств и «Автоматизация электропривода». Лабораторные работы проводятся на ПК с использованием средств TurboС V3.0 или BuilderC++ V5.0 (или V6.0) или любого другого транслятора языка С++.
При подготовке к лабораторной работе необходимо ознакомиться с материалами лекций, начитанных по теме лабораторной работы, а также с предложенной литературой. Список предлагаемой литературы представлен в конце данных методических указаний.
В лабораторных работах даются теоретические сведения по рассматриваемой теме и примеры программ для данного класса задач. Все программы снабжены комментариями и подробными объяснениями. Для выполнения лабораторных работ разработаны тридцать вариантов индивидуальных заданий. Вариант задания выдается преподавателем в начале семестра или перед выполнением каждой лабораторной работы.
Тематика лабораторных работ охватывает основные моменты разработки оптимальных алгоритмов решения поставленных задач и программирования средствами языка С++, помогает студентам освоить приемы работы с массивами, структурами, функциями, файлами и строками. Для закрепления изученного материала и самопроверки студентами полученных знаний в каждой лабораторной работе дается перечень контрольных вопросов.
Общие требования к отчетам по лабораторным работам таков: отчет должен содержать:
— титульный лист,
— название лабораторной работы,
— цель и задание,
— текст программы (или несколько текстов программ), снабженный комментариями,
— результаты работы программы.
Лабораторная работа № 1.
ВЫЧИСЛЕНИЕ СУММЫ БЕСКОНЕЧНОГО РЯДА С ЗАДАННОЙ ТОЧНОСТЬЮ.
1. Цель работы: ознакомиться с текстовым редактором С++; освоить простейшие языковые конструкции ввода — вывода данных; приобрести практические навыки составления и отладки программ с простыми переменными; знать основные предопределённые языком типы данных и правила их описания; усвоить арифметические и логические операции; усвоить способы организации циклических вычислений и операторы управления.
2. Указания по подготовке к работе:
Необходимо ознакомиться с основными предопределёнными типами данных (целочисленные типы, вещественные типы, тип char и логический тип (bool)) и операторами управления (условными и цикла), а также операторами ввода-вывода. [см. лекцию 4, 5, 7, 8].
3. Теоретическая часть:
Часто в математических вычислениях возникает необходимость определить сумму бесконечного ряда с заданной точностью. На такие задачи налагается одно жесткое условие: ряд должен быть сходящимся, т.е. абсолютное значение текущего элемента ряда должно быть меньше абсолютного значения его предыдущего элемента.
В подобных случаях удобно пользоваться итерационными циклами, реализуемыми операторами цикла с предварительным и последующим условиями.
В противном случае условие выхода из цикла никогда не будет выполнено и цикл станет бесконечным.
Пример: написать программу вычисления суммы бесконечного ряда с точностью eps=0.001:
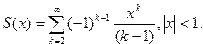
Этот ряд сходится при |x|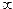 , а так как он знакопеременный, то его предел равен 0 (значения его элементов стремятся к нулю).Для достижения заданной точности требуется суммировать члены ряда, абсолютная величина которых больше eps. Для сходящегося ряда модуль члена ряда C
, а так как он знакопеременный, то его предел равен 0 (значения его элементов стремятся к нулю).Для достижения заданной точности требуется суммировать члены ряда, абсолютная величина которых больше eps. Для сходящегося ряда модуль члена ряда C 
 при увеличении n
при увеличении n  стремится к нулю. При некотором n неравенство
стремится к нулю. При некотором n неравенство
| C 
 |
| 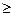 eps перестает выполняться и вычисления прекращаются.
eps перестает выполняться и вычисления прекращаются.
Общий алгоритм решения этой задачи очевиден: требуется задать начальное значение суммы ряда, затем многократно вычислять очередной член ряда и добавлять его к ранее найденной сумме. Вычисления заканчиваются, когда величина очередного члена ряда станет меньше заданной точности. Алгоритм представим в виде блок-схемы (см. рис.1). Как видно из рис.1. каждый блок имеет один вход и один выход за исключением условного блока (ромб), который имеет два выхода. Выходы могут располагаться или по обе стороны блока, или любой из них по центру. Ошибки в этом нет. Выходы обязательно должны иметь названия: либо «истина» («да», «+»), либо «ложь» («нет», «-«). Это необходимо для однозначного понимания логики алгоритма.
В блок-схеме запрещено указывать команды, операции, функции конкретного языка программирования. Все действия должны быть описаны математически, а если это не возможно, то словесно.
Линии потока, указывающие последовательность выполнения действий, должны располагаться параллельно границам листа (только горизонтально или вертикально), не могут пересекаться друг с другом. Если линии указывают естественный ход выполнения действий (сверху вниз и слева направо), то их можно не обозначать стрелками, а если снизу вверх или справа налево, то стрелками обозначать обязательно.
Блоки, кроме блоков «начало» и «конец» («останов»), можно нумеровать, что также улучшает наглядность схемы.
До выполнения программы предсказать, сколько членов ряда потребуется просуммировать, невозможно. В цикле такого рода есть опасность, что он никогда не завершиться – как из-за возможных ошибок в вычислениях, так и из-за ограниченной области сходимости ряда. Поэтому для надежности программы нужно предусмотреть аварийный выход из цикла с печатью предупреждающего сообщения по достижении некоторого максимально допустимого количества итераций. В качестве признака сходимости ряда будем использовать булеву переменную flag. В случае, если ряд расходится, значение этой переменной обнулится (примет значение «ложь»). Напомним, что для расходящегося ряда значение суммы его элементов не может быть подсчитано, а, следовательно, результат не должен быть выведен. Однако, в ранних версиях компиляторов языка С++ нет такого типа данных, как булевый, поэтому вместо него можно использовать либо тип int или самый короткий тип char.
#include
#include
#include
void main(){
int k, const Max = 500; // максимально допустимое количество
// итераций
float sum = 0., eps = 1.0e-3, s, x;
bool flag = true; // char flag = 1;
printf (“Введите значение х
// cout
scanf(“%f”, x); // можно использовать cin…
k = 2; // согласно условию
s = 5*eps; // значение нужно для входа в цикл
while (fabs(s)eps)
{s = pow(x,k)/(k-1.); //вычисление абсолютного значения
// текущего элемента ряда
if ((k-1)%2 = = 0) // определение знака элемента ряда
sum=sum+s;
else
sum=sum-s;
k++;
if (kMax){
printf(“Ряд расходится!”);
flag = false; // flag = 0;
break;
}
}
if (flag) printf(“Сумма равна %f\n”, sum); // if (flag == 1)…
}
Прямое вычисление члена ряда по приведенной выше формуле имеет два недостатка, которые делают этот способ непригодным. Первый недостаток – большая погрешность вычислений. При возведении в степень (а особенно при вычислении факториала) можно получить очень большие числа, при делении больших чисел друг на друга произойдет потеря точности, поскольку количество значащих цифр, хранимых в ячейке памяти, ограничено. Второй недостаток связан с эффективностью (рациональностью) вычислений: при вычислении очередного члена ряда нам уже известен предыдущий, поэтому вычислять каждый член ряда по исходной формуле нерационально.
Для уменьшения количества выполняемых действий следует воспользоваться рекуррентной формулой получения последующего члена ряда через предыдущий
Rn = 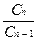 , где R – некоторый множитель
, где R – некоторый множитель
тогда
Cn=R  Cn-1.
Cn-1.
Подставив в эту формулу значения Cn и C 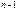 получим:
получим:
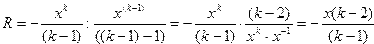
Множитель (-1)k-1 сокращается и в итоге получается просто «-», который мы, опустив эти вычисления, сразу указали в рекуррентном соотношении.
Вот эту формулу мы подставим в текст программы и получим:
. . .
k = 3; // увеличили номер члена ряда на 1
s = — x*x; // нашли по формуле значение 1-го члена ряда
while (fabs(s)eps)
{sum+=s;
s*=-( x*(k-2.)/(k-1.)); //вычисление значения
// текущего элемента ряда по предыдущему
k++;
if (kMax){
cout
flag = false; // или flag = 0;
break;
}
} . . .
Максимально допустимое количество итераций удобно задать с помощью именованной константы (Max). Для аварийного выхода из цикла применяется оператор break, который выполняет выход на первый после цикла оператор.
Поскольку выход как в случае аварийного, так и в случае нормального завершения цикла происходит в одну и ту же точку программы, вводится булева переменная flag, которая предотвращает печать значения функции после выхода из цикла, в случае, когда точность вычислений не достигнута. Создание подобных переменных-«флагов», принимающих значение «истина» в случае успешного окончания вычислений и «ложь» в противном случае, является распространенным приемом программирования.
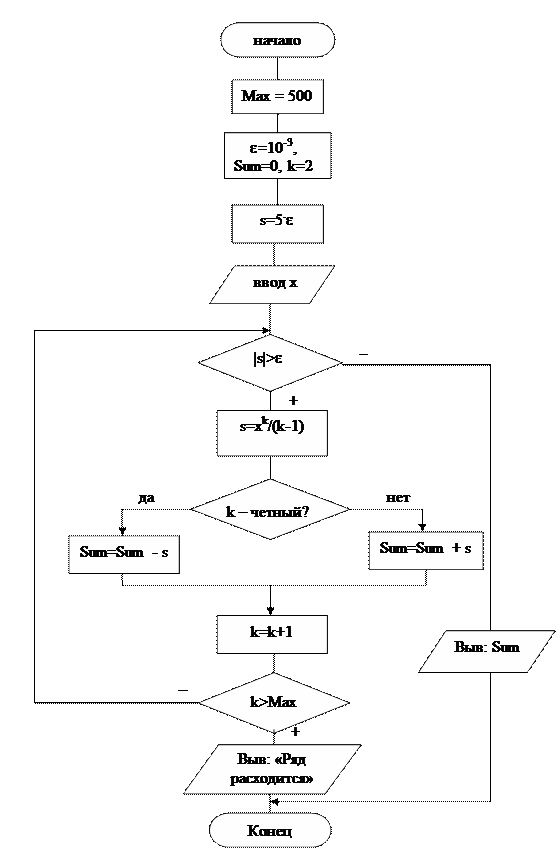
Рис.1. Блок-схема нахождения суммы знакопеременного бесконечного ряда
Задание.
Для выданного преподавателем варианта задачи написать и отладить программу на языке С++ расчета суммы знакопеременного ряда с использованием рекуррентного соотношения.
Измените программу так, чтобы она печатала не только значения аргумента и функции, но и количество просуммированных членов ряда.
Реализуйте ту же логику без специальной булевой переменной, объединив проверку обоих вариантов выхода из цикла в заголовке.
5. Требования к отчету по лабораторной работе:
Отчет должен содержать:
1) расчеты рекуррентного множителя для Вашей задачи;
2) блок-схему алгоритма задачи
3) распечатки или тексты программ с комментариями.
6. Варианты индивидуальных заданий:
.
1. Вычислить сумму ряда
S= 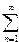
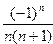
с точностью  =10-2.
=10-2.
2. Вычислить сумму ряда
S= 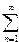
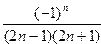
с точностью  = 10-3.
= 10-3.
3. Вычислить сумму ряда
S= 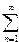
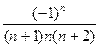
с точностью  =10-4.
=10-4.
4. Вычислить сумму ряда
S= 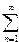
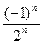
с точностью  =10-4.
=10-4.
5. Вычислить сумму ряда
S= 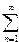 n
n 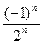
с точностью  =10-5.
=10-5.
6. Вычислить сумму ряда
S= 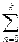 (-1)n
(-1)n 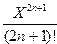
с точностью  =10-3 , X0=0.3
=10-3 , X0=0.3  .
.
7. Вычислить сумму ряда
S= 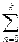 (-1)n
(-1)n 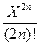
с точностью  =10-3 , X0=
=10-3 , X0=  /9.
/9.
8. Вычислить сумму ряда
S= 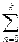
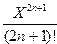 (-1)n+1
(-1)n+1
с точностью  =10-8, X0=1.6 .
=10-8, X0=1.6 .
9. Вычислить сумму ряда
S= 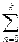
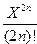 (-1)n+1
(-1)n+1
с точностью  =10-8, X0=1.22.
=10-8, X0=1.22.
10. Вычислить сумму ряда
S= 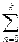 (-1)n
(-1)n 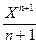
с точностью  =10-4, X0=0.6785.
=10-4, X0=0.6785. 
11. Вычислить сумму ряда
S= 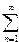
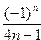
с точностью  =10-3.
=10-3.
12. Вычислить сумму ряда
S= 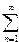 (-1)n+1
(-1)n+1 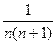
с точностью  =10-4.
=10-4.
13. Вычислить сумму ряда
S= 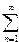 n
n 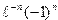
с точностью  =10-3.
=10-3.
14. Вычислить сумму ряда
S= 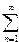 n3n-1(1/4)n-1(-1)n
n3n-1(1/4)n-1(-1)n
с точностью  =10-3.
=10-3.
15. Вычислить сумму ряда
S= 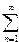
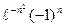
с точностью  =10-5.
=10-5.
16. Вычислить сумму ряда
S= 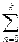 (-1)n
(-1)n 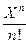
с точностью  =10-5, в точке X0=2.44.
=10-5, в точке X0=2.44.
17. Вычислить сумму ряда
S= 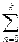
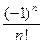
с точностью  =10-6.
=10-6.
18. Вычислить
S=4 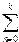 (-1)n
(-1)n 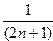
с точностью  =10-2.
=10-2.
19. Вычислить сумму ряда
S= 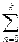
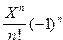
с точностью  =10-4 в точке X0=2.334.
=10-4 в точке X0=2.334.
20. Вычислить сумму ряда
S= 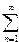
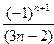
с точностью  =10-3.
=10-3.
21. Вычислить сумму ряда
S=2 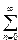
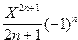
с точностью  =10-4 в точке X0=0.4357.
=10-4 в точке X0=0.4357.
22. Вычислить сумму ряда
S= 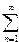
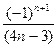
с точностью  =10-2.
=10-2.
23. Вычислить сумму ряда
S= 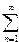
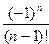
с точностью  =10-4.
=10-4.
24. Вычислить сумму ряда
S= 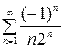
с точностью  =10-6.
=10-6.
25. Вычислить сумму ряда
S= 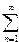
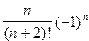
 с точностью
с точностью  =10-6.
=10-6.
26. Вычислить сумму ряда
S= 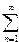
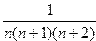
с точностью  =10-4.
=10-4.
27. Вычислить сумму ряда
S= 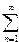
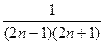
с точностью  =10-4.
=10-4.
28. Вычислить сумму ряда
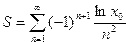
с точностью 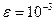 , в точке
, в точке 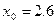
29. . Вычислить сумму ряда
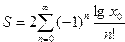
с точностью 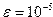 , в точке
, в точке 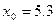
30. . Вычислить сумму ряда
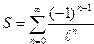
с точностью 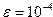
Контрольные вопросы.
1. Как ввести начальные значения переменных.
2. Какое место расположение операторов описания типа в программе.
3. Какие формы представления чисел существуют в С++.
4. Какая последовательность выполнения операций в выражениях.
5. Что понимается под термином « тело цикла ».
6. Какого типа могут быть метки в операторе swith.
7. Какие существуют формы записи условного оператора? В чём их различие?
Лабораторная работа № 2.
Статьи к прочтению:
[pascal] написать программу, вычисляющую сумму ряда
Похожие статьи:
-
Будем теперь рассматривать бесконечную сумму вида . Это выражение называется функциональным рядом. При различных значениях x из функционального ряда…
-
Вычисление определенного интеграла с заданной точностью
Задача вычисления определенного интеграла формулируется следующим образом: вычислить I= c точностью ? при известных значения пределов интегрирования a,…
