Арифметические операции в системе с плавающей точкой

Введение

Решение задачи на ЭВМ предполагает, что математические формулы, алгоритмы будут адекватно преобразованы на язык машинных команд. Однако, арифметические операции на ЭВМ не обладают теми же свойствами, что и математические операции, например, в условиях машинной арифметики в общем случае нельзя утверждать, что для любых трех чисел : .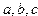

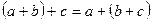Машинная арифметика имеет свои характерные особенности. При обсуждении их необходимо учитывать два важных обстоятельства:

1. Машинная арифметика отличается от арифметики «карандаша и бумаги». В ручных вычислениях промежуточные результаты непосредственно доступны для обозрения, и точность вычислений можно изменять в соответствии с требованиями момента, кроме того, можно при проверке вычислений последовательно просмотреть весь процесс от начала до конца, что очень важно при «отлавливании» возможных ошибок. В машинной арифметике, как правило, доступа ко всем промежуточным вычислениям не имеется, что усложняет процесс нахождения ошибок. Кроме того, каждое число имеет фиксированное количество разрядов, которого в известных случаях может не хватать для получения приемлемой точности.

2. Ручные вычисления обычно не бывают длинными, тогда как машинный процесс может состоять из миллионов шагов. Ничтожно малые ошибки, которыми в коротком вычислении можно было бы пренебречь, накапливаясь в протяженном процессе, могут приводить к разрушительным последствиям. Кроме того, методы, вполне удовлетворительные для малых задач, могут быть безнадежно неэффективными для больших задач того же типа.

Отличия машинной арифметики от арифметики «реальной» могут казаться несущественными, однако не таковы последствия этих отличий.

Представление чисел в ЭВМ

В машинных вычислениях участвуют числа двух типов: целые и вещественные («с плавающей точкой»). Первые компьютеры допускали только целочисленную арифметику. Для представления дробей использовалась воображаемая точка в фиксированной позиции внутри целого числа. Это называлось «арифметикой с фиксированной точкой». В 1954 г. фирма IBM начала производство компьютера 704, в котором все алгоритмы для вещественных чисел были реализованы как машинные команды, что чрезвычайно упрощало использование нецелочисленной арифметики. Арифметика с фиксированной точкой более не является стандартным режимом компьютера, исключение составляют лишь некоторые специализированные устройства. Стандартна аппаратно реализованная арифметика с плавающей точкой.

Множество чисел с плавающей точкой 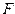характеризуется 4-мя параметрами: числом разрядов 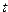, основанием системы счисления 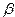, границами 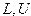изменения показателя. Каждое число 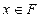представляется в виде:

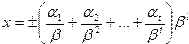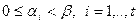где — целые числа такие, что , а 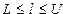. Число 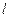называется показателем, 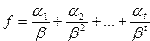— дробной частью или мантиссой.

Если для любого ненулевого числа 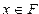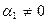, то система называется нормализованной.

Множество 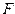является конечным, а значит имеет наибольший и наименьший по модулю элементы в отличие от множества действительных чисел 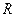. Числа, меньшие по модулю минимального ненулевого числа из множества 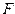, представляются в ЭВМ нулем. Минимальное положительное число 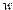, которое может быть представлено в системе с плавающей точкой 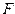, иногда называется машинным нулем.

В силу конечности множества 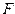при представлении заданного ненулевого числа 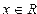в системе чисел с плавающей точкой могут возникнуть 4 ситуации:

1) число 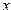по модулю больше максимального из чисел множества 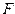— переполнение порядка; для большинства компьютеров вычисление на этом заканчивается;

2) число 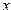по модулю меньше минимального по модулю ненулевого из чисел множества 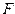— исчезновение порядка; это событие обычно не имеет таких катастрофических последствий, как переполнение, и многие компьютеры заменяют результат нулем без какого-либо указания на то, что это произошло. Однако есть вычисления, для которых такой факт важен;

3) число 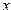совпадает с одним из чисел множества 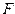— в этом случае 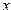представляется в ЭВМ точно;

4) число 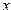находится в границах представления чисел данной системы 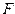, но не совпадает ни с одним из чисел 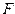— в этом случае оно приближается одним из чисел множества 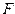по некоторому правилу, в результате возникает погрешность.

С точки зрения точности представления чисел в ЭВМ наибольший интерес представляет ситуация 4). В современных ЭВМ наиболее широко представлены два способа приближения чисел: округление и усечение.

Округление числа 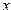— замена этого числа ближайшим к нему числом 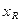из множества 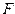; усечение включает в себя нормализацию числа 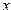и последующее отбрасывание лишних разрядов, в результате чего получается .

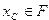Задание. Какой способ приближения является более точным, на сколько? Почему?

Арифметические операции в системе с плавающей точкой

Конечность множества 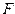приводит к особенностям машинной арифметики, отличающим ее от обычной известной с первого класса арифметики, законы которой, в общем случае, в 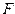не выполняются.

Для двух заданных чисел 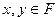результат выполнения арифметических операций (сложения, вычитания, умножения, деления) при вычислении в системе с плавающей точкой будем обозначать: 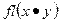. Идеальным для выполнения таких операций является случай, когда сама операция над 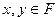выполняется точно, а затем результат либо округляется, либо усекается. Это является основной гипотезой машинной арифметики и реализовано практически на всех ЭВМ.Для выполнения арифметической операции обычно выделяются дополнительные разряды, полученный результат нормализуется, а затем выполняется округление или усечение.

Пример. Пусть 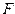— множество чисел с плавающей точкой, для которого 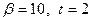. Найдем сумму трех чисел: 0.12+0.17+0.87. Сложение можно провести двумя способами, которые, с точки зрения обычной арифметики, являются эквивалентными: (0.12+0.17)+0.87 или 0.12+(0.17+0.87).

Таким образом, в рассмотренной системе с плавающей точкой (0.12+0.17)+0.87? 0.12+(0.17+0.87), что говорит о нарушении сочетательного закона сложения.

В общем случае определение системы чисел с плавающей точкой приводит к тому, что результат арифметического выражения в ней зависит от порядка выполнения операций. Это значит, одному алгоритму, «записанному на бумаге», соответствует множество «машинных» алгоритмов, в каждом из которых другой порядок выполнения действий и, следовательно, может быть другой результат.

При сложении машинных чисел различной величины результат может оказаться точно равен одному из слагаемых. Вполне можно было бы, не изменяя результата, заменить меньшее число нулем. Наименьшее число с плавающей точкой, которое при сложении с числом 1 дает результат, больший, чем 1, часто называется машинным эпсилоном и обозначается 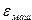. Конкретное значение 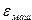зависит от того, какая арифметика используется – с округлением или усечением.

Машинный эпсилон определяет относительную погрешность арифметики компьютера. Есл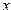и и 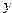— два положительных числа с плавающей точкой и 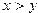, то их сумму можно записать в виде

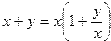Очевидно, что при 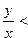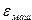сумма с плавающей точкой чисел 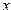и 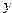совпадает с 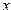. Более тщательные исследования показывают, что относительная погрешность сложения чисел с плавающей точкой ограничена величиной .

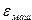Задание. Привести пример системы 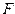и двух чисел в ней, для которых результат их сложения точно равен одному из слагаемых.

Важнейшие свойства вычислений с плавающей точкой:

1. Множество чисел с плавающей точкой конечно.

2. Существует наибольшее число с плавающей точкой.

3. Существует наименьшее положительное число с плавающей точкой.

4. Арифметические операции над числами с плавающей точкой не всегда приводят к точно представимым результатам, поэтому результаты приходится усекать или округлять до ближайшего числа с плавающей точкой.

5. Константа 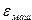есть наименьшее число с плавающей точкой, для которого 1.0+ 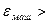1.0 в арифметике с плавающей точкой. Это число характеризует относительную точность машинной арифметики.

Статьи к прочтению:

Сложение чисел с плавающей точкой

Похожие статьи: